
- •1.Сызықты емес теңдеулерді шешудің сандық әдістері
- •2.Сандық интегралдау есебі
- •3. Сызықты емес теңдеулерді шешудің сандық әдістері
- •10.Функцияны интерполяциялау
- •12.Шекті-айырымдық схемалардың орнықтылығы мен жинақтылығы туралы түсінігі. Схеманың орнықтылығын зерттеу, фон Нейман әдісі.
- •14.Эйлер схемасының бірінші дифференциалдық жуықтауы (бдж немесе модификацияланған теңдеу). Бдж көмегімен схеманың орнықтылығын зерттеу.
- •16. Лакс, Лакс-Вендроф, «Чехарда», Мак-Кормак схемалары. Аппроксимация және басқа қасиеттері.
- •18. Екі өлшемді тасымал және/немесе диффузия теңдеулері үшін айқындалмаған айырымдық схемалар. Кранк-Николсон схемасы. Айнымалы бағыт әдісі.
- •27. Бюргерс теңдеуі үшін Лакс-Вендроф схемасы, Мак-Кормак схемасы. Олардың қасиеттері.
10.Функцияны интерполяциялау
F(x) функциясының белгілі мәндері келесі кестені құрсын.
-
хi
X0
X1
…
x
(4.1)
nF(xi)
Y0
Y1
…
yn
[x0, xn] аралығында жататын, бірақ xi-лердің ешқайсысымен сәйкес келмейтін х-тегі функция мәнін табу керек болсын.
Әдетте функцияның аналитикалық өрнегі берілсе, онда х-тің орнына мәнін қойып функция мәнін есептей салуға болатын. Кей жағдайда функцияның аналитикалық өрнегі мүлде белгісіз болуы немесе есептеуге көп уақытты қажет етуі мүмкін. Осындай жағдайларда берілген кесте бойынша f функциясына жуық F жуықтаушы функцияны құрады:
f(x)=F(x) (4.2)
Құрылған жуықтаушы функция келесі шарттарды қанағаттандыруы керек:
F(x0)=y0, F(x1)=y1, F(x2)=y2, …. , F(xn)=yn (4.3)
Мұндай есепті функцияны интерполяциялау есебі деп атайды. Ал х0, x1, x2, … , xn нүктелерін – интерполяциялау тораптары немесе түйіндері деп атайды.
F(x) интерполяиялаушы функцияны n дәрежелі көпмүшелік түрінде іздейді: Лагранж, Ньютон, Гаусс, Бессель, Стирлинг, т.б.
Егер интерполяциялық түйіндердің бір бірінен ара қашықтықтары тұрақты емес болса, Лагранждың көпмүшелігі, тұрақты болса – Ньютоннның көпмүшеліктері қолданылады.
Лагранждың интерполяциялық көпмүшелігі
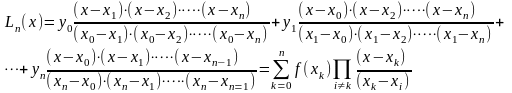 (4.4)
(4.4)
Кей жағдайда есептеу процесін жеңілдету үшін x=at+b, xj=atj+b j=0,1,…,n сызықты алмастыруын жасау арқылы Лагранж коэффициенттерінің инварианттылығын қолдануға болады, онда (4.4)-формула келесі түрге келеді:
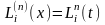 (4.5)
(4.5)
12.Шекті-айырымдық схемалардың орнықтылығы мен жинақтылығы туралы түсінігі. Схеманың орнықтылығын зерттеу, фон Нейман әдісі.
Бір өлшемді диффузия теңдеуі үшін УАКО схемасын пайдаланайық.
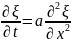 (1)
(1)
УАКО: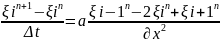 (2)
(2)
Немесе
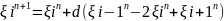 (3)
(3)
Мұндағы

Фурье қатарына жіктеп жазатын болсақ
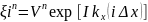 (4)
(4)
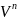 -амплитуда
-амплитуда
 -толқын
саны.
-толқын
саны.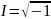
Егер
фазалық бұрышты
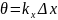 енгізсек,онда
(4)теңдеу
мына түрге келеді.
енгізсек,онда
(4)теңдеу
мына түрге келеді.
 (5)
(5)
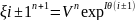 (6)
(6)
(5) пен (6) --> (3)
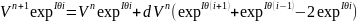 (7)
(7)
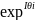 -бөлгеннен
кейін
-бөлгеннен
кейін
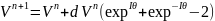 (8)
(8)
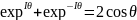 (9)
(9)
G-көшу көпмүшелігі
G=1-2d(1- )
(10)
)
(10)
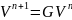 (11)
(11)
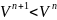
11
теңдеудің
шешімі барлық
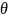 үшін шектелген күйінде қалу үшін мына
шарт орындалуы керек
үшін шектелген күйінде қалу үшін мына
шарт орындалуы керек
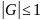 (12) (орнықтылық
шарт)
(12) (орнықтылық
шарт)
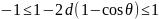
Оң жақ бөлігі барлық -да орындалады.Ал сол жақтағы теңсіздік
max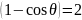 кезінде
критикалық болады.Сондықтан
кезінде
критикалық болады.Сондықтан
d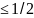 немесе
немесе
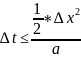 (13)
(13)
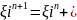
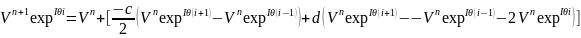 (14)
(14)
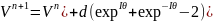 (15)
(15)
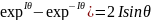 (16)
(16)
G=1-2d(1- )-ICsin (17)
17 теңдеуді (1-2d) нүктесінде орналасқан жарты осьтерi С ж/е 2d эллипс тендеуіне сәйкес келеді.
14.Эйлер схемасының бірінші дифференциалдық жуықтауы (бдж немесе модификацияланған теңдеу). Бдж көмегімен схеманың орнықтылығын зерттеу.
1-ретті қарапайым дифференциалдық теңдеу (ҚДТ) жалпы түрде келесідей жазылады:
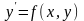 (6.1)
(6.1)
Бұл теңдеуге қатысты негізгі есеп Коши есебі деп аталады: (6.1)-теңдеудің
y(x0) = y0 (6.2)
бастапқы шартты қанағаттандыратын
y=y(x) (6.3)
түріндегі шешімін табу.
Басқа сөзбен айтқанда координаттары M0(x0,y0) нүктесінен өтетін (6.3) - интегралдық қисықты табу керек.
Егер
(6.1)-дің
оң жағындағы
 функциясы
R облысында
анықталған
және
функциясы
R облысында
анықталған
және
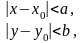
теңсіздігімен
анықталса, онда
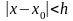 ,
(h –тұрақты
сан) аймағында (6.2)
– бастапқы шартты қанағаттандыратын
(6.3)-
түріндегі болмағанда бір түбір табылады.
Бұл
шешім
жалғыз
болады,
егер
R облысында
Липшиц шарты
,
(h –тұрақты
сан) аймағында (6.2)
– бастапқы шартты қанағаттандыратын
(6.3)-
түріндегі болмағанда бір түбір табылады.
Бұл
шешім
жалғыз
болады,
егер
R облысында
Липшиц шарты
 орындалса,
мұндағы
N –a мен
b-дан
тәуелді
Липшиц
тұрақтысы.
Егер
R облысында
орындалса,
мұндағы
N –a мен
b-дан
тәуелді
Липшиц
тұрақтысы.
Егер
R облысында
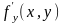 туындысы
бар
болса,
онда
туындысы
бар
болса,
онда
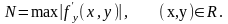 .
.
n–ші
ретті
дифференциалдық
теңдеу
үшін
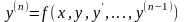 Коши
есебі
Коши
есебі
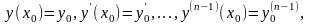 мұндағы
мұндағы
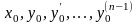 –
берілген
сандар,
шарттарын қанағаттандыратын (6.3)-түрдегі
шешімді табу керек деп қойылады.
–
берілген
сандар,
шарттарын қанағаттандыратын (6.3)-түрдегі
шешімді табу керек деп қойылады.
Егер х-ті уақыт деп қарастырсақ, ал у1,…,уn – әлдебір механикалық жүйенің жалпылама координаттары десек, онда Коши есебінің келемі аспектісін аламыз: механикалық жүйені басқаратын дифференциалдық теңдеуді біле отырып, сондай-ақ оның бастапқы х0 уақыт моментіндегі күйін біле отырып, жүйенің кез келген х уақыт моментіндегі күйін анықтау керек болады.
Мұндай есепті шешудің сандық әдістері екіге бөлінеді:
Бірқадамды сандық әдістер – y=f(x) қисығында келесі нүктедегі функция мәнін табу үшін оның алдындағы бір ғана қадамдағы мән берілген жағдайда қолданылады. Оларға – Рунге-Кутта, Эйлер, Эйлер-Коши әдістері жатады;
Көпқадамды сандық әдістер - y=f(x) қисығында келесі нүктедегі функция мәнін табу үшін оның алдындағы бірнеше қадамдардағы (нүктелердегі) мәндер берілген жағдайда немесе мәндер кестесін толықтыру жағдайында қолданылады. Оларға жататындар – Адамс, Милн әдістері:
Эйлер әдісі
Коши есебін шешудің бұл әдісі бірінші ретті дифференциалдық теңдеуді интегралдауға мүмкіндік береді. Бұл әдістің дәлдігі төмен. Сондықтан практикада көп қолданылмайды. Бірақ бұл әдістің негізінде басқа тиімді, бірақ күрделі әдістерді меңгеру жеңілдейді.
(6.1)-(6.2) Коши есебі берілсін.
Геометриялық мағынасы: һ қадам таңдап алып берілген аралықта бірдей қадаммен нүктелер жиынын құраймыз:
xi=x0+ih (i=0,1,2,…). (6.4)
M0(x0,y0) нүктесінен өтетін ізделінді y=y(x) интегралдық қисықты төбелері Mi (xi,yi) (i=0,1,2,…) болатын Эйлер сынықтарымен M0M1M2… алмастырылады:
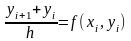 (6.5)
(6.5)
Әрбір MiMi+1 сынықтары бағыты Mi нүктелерінен өтетін (6.1)-теңдеумен берілген интегралдық қисықтың бағытымен беттеседі.
Сонда есептеу формуласы келесі түрде жазылады:
Yi+1=yi+yi, (6.6)
yi=hf(xi,yi) (i=0,1,2,…)
Әдіс теңдеулер жүйесіне де қолданылады. Ол 2-мысалмен келтірілген.
1-Мысал:
Эйлер
әдісін қолданып [0,1] аралығында h=0,2
қадаммен
 теңдеуін және у(0)=1 бастапқы шартты
қанағаттандыратын мәндер кестесін құру
керек болсын.
теңдеуін және у(0)=1 бастапқы шартты
қанағаттандыратын мәндер кестесін құру
керек болсын.
Есептеу нәтижелері 15-кестеде келтірілген. Кестенің толтырылуы:
Бірінші
жолға i=0 болғанда бастапқы мәндер
жазылады: x0=0;
y0=1,0000.
Үтірден кейін мәнді цифрларды жоғалтпау
үшін 4 орын сақтап отырайық. Осы мәндер
және (6)- формула бойынша f(x0,y0)=1,
сосын
 ,
у1=1+0,2=1,2
мәндері есептеледі.
,
у1=1+0,2=1,2
мәндері есептеледі.
Екінші
жолға i=1 болғанда x1=0.2,
y1=1.2000
мәндері жазылады. Осы мәндерді қолданып
f(x1,y1)=0.8667
мәні,
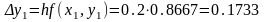 мәні есептеледі. Сосын
мәні есептеледі. Сосын
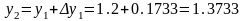 мәнін анықтауға болады. Дәл осылайша
i=2,3,4,5 болғандағы есептеулерді анықтауға
болады.
мәнін анықтауға болады. Дәл осылайша
i=2,3,4,5 болғандағы есептеулерді анықтауға
болады.
Кестенің
ең соңғы бағанында салыстыру үшін
теңдеудің дәл шешімінің
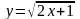 мәндері келтірілген. Кестеден абсолютті
қателіктің мәні е=0,0917, салыстырмалы
қателігінің 5% екендігі көрінеді.
мәндері келтірілген. Кестеден абсолютті
қателіктің мәні е=0,0917, салыстырмалы
қателігінің 5% екендігі көрінеді.
