
- •1.Сызықты емес теңдеулерді шешудің сандық әдістері
- •2.Сандық интегралдау есебі
- •3. Сызықты емес теңдеулерді шешудің сандық әдістері
- •10.Функцияны интерполяциялау
- •12.Шекті-айырымдық схемалардың орнықтылығы мен жинақтылығы туралы түсінігі. Схеманың орнықтылығын зерттеу, фон Нейман әдісі.
- •14.Эйлер схемасының бірінші дифференциалдық жуықтауы (бдж немесе модификацияланған теңдеу). Бдж көмегімен схеманың орнықтылығын зерттеу.
- •16. Лакс, Лакс-Вендроф, «Чехарда», Мак-Кормак схемалары. Аппроксимация және басқа қасиеттері.
- •18. Екі өлшемді тасымал және/немесе диффузия теңдеулері үшін айқындалмаған айырымдық схемалар. Кранк-Николсон схемасы. Айнымалы бағыт әдісі.
- •27. Бюргерс теңдеуі үшін Лакс-Вендроф схемасы, Мак-Кормак схемасы. Олардың қасиеттері.
2.Сандық интегралдау есебі
Сандық интегралдау инженерлік және ғылыми деректерді анализдеу немесе сараптау үшін қажетті. Интегралды классикалық әдістермен аналитикалық түрде алу мүмкін болмаған жағдайларда сандық интегралдау есебі қойылады. Кейде интеграл астындағы функция өте күрделі, кейде функцияның кесте лық мәндері ғана берілуі мүмкін.
Сандық интегралдауды сандық квадратура деп те атайды. Ал қолданылатын формулалар квадратуралық формулалар деп аталады.
Сандық интегралдау да дәл және жуықтау болып екіге бөлінеді.
Егер абсцисса өсі бойынан алынатын нүктелер бірқалыпты орналасатын болса, онда Ньютон – Котестің дәл квадратуралық формулалары қолданылады, басқа жағдайда жуықтау – Гаусс формулалары қолданылады.
Сандық интегралдаудың негізгі идеясы - интеграл астындағы функцияны [a,b] аралығында интерполяциялық полиномға жіктеу және полиномның әр мүшесін интегралдау арқылы есептеу процесін жеңілдету.
Интегралдың қателігін төмендету үшін интеграл астындағы функция анықталған [a,b] аралығы h қадаммен бірнеше аралыққа бөлу керек: xi+1-xi=h, i=1,2,…,n-1. Қадам тұрақты болған жағдайды қарастырайық.

түрдегі интеграл берілсін. Дәл әдістерге Ньютон-Котес квадратуралық формулалары жататыны жоғарыда айтылған.
3. Сызықты емес теңдеулерді шешудің сандық әдістері
Сандық әдістердің бір бөлімі «бір өлшемді сызықты емес теңдеулер» болып табылады. Физикалық және басқа да құбылыстардың теңдеумен сипатталатыны белгілі. Сол теңдеуді классикалық математикалық формуламен шешу мүмкін емес жағдайлар бар. Бұл уақытта практикада сандық әдістерге жататын әдістермен шешілетінін дәлелдеу керек. Әрине ең алдымен құрылған теңдеудің қай аралықта анықталғандығын, үзіліссіздігін, түбірінің барлығын, оның жалғыздығын дәлелдейтін аргументтерді бақылау керек. Осы этаптан өткеннен кейін ғана есепті осы теңдеуге қолдануға келетін алгоритм көмегімен шығаруға болады.
Сызықты емес теңдеулер екі түрлі:
Алгебралық;
Трансцендентті;
Алгебралық теңдеулер деп алгебралық көпмүшеліктерден тұратын теңдеулерді айтады. Олардың шешімдері көбіне нақты сан болады.
Трансцендентті теңдеу деп құрамында тригонометриялық немесе арнаулы функцялары бар теңдеуді айтады.
Сызықты емес теңдеуді сандық шешу екі тәсілден ([1] қараңыз) тұрады.
1 Тура тәсіл - есепті математикалық дәлелденген бір формулаға қою арқылы тікелей шығару;
2 Итерациялық тәсіл – есепті формула көмегімен бастапқы жуықтауды беру арқылы жуықтап, біртіндеп шығару;
Тура тәсілмен шығарылған есептер дәл мәнді береді. Ал итерациялық тәсілмен шешілген есептер есептің жуық мәнін береді .Мұның ішінде итерациялық әдістер сандық әдіске жатады.
Бір өлшемді сызықты емес теңдеуді шешудің келесі әдістері бар.
1 Кесіндіні қақ бөлу - дихотомия әдісі деп аталады;
2 Хорда әдісі;
3 Жанама әдісі немесе Ньютон әдісі;
4 Қарапайым итерациялық әдіс немесе жәй итерация әдісі т.б.;
4.Сызықты алгебралық теңдеулер жүйесін шешудің тура және итерациалық әдістері. Гаус әдісі.Якоби және Зейдель әдістері. Сызықты алгебралық теңдеулер жүйесін шешудің тура әдістері.Сызықты алгебралық теңдеулер жүйесін шешудің Крамер әдісі- бойынша сызықты теңдеулер жүйесін шешуде жүйелі түрде келесі алгоритм орындалады:
1. Жүйені матрицалы түрде жазады (егер бұл әлі істелмесе).
2. Жүйенің басты анықтауышын табады:
Сызықты алгебралық теңдеулер жүйесін шешудің Гаусс әдісі-Гаусс әдiсiн қолдану арқылы, жүйенi белгiсiздерiнен бiртiндеп арылады және жүйенi үшбұрыш түрiне алып келедi.Гаусс әдісінің басқа атауы шығады – белгісіздерді сатылы алып тастау әдісі.
Сызықты алгебралық теңдеулер жүйесін шешудің «Бас элементті таңдау схемасы» әдісі-Гаусс әдісінің өзгертілген түрінің бірі (модификациясының бірі) – бас элементті таңдау схемасы болып табылады. Мұнда белгісіздерді біртіндеп шығаруда бөлу орындалатын диагоналдық элементтердің нөлге тең болмау шарты одан да қатаң шартпен, яғни қалған к-шы бағандағы элементтердің ішінен модулі ең үлкені таңдалып, акк элементінің орнына баратындай етіп теңдеулердің орнын алмастыру қажет шарты қойылады.
Қуалау әдісі-Теңдеулер жүйесінің матрицасы үш диагоналды болған жағдайда Гаусс әдісінің модификациясы «Қуалау әдісін» қолданады. Мұндай теңдеулер жүйесі инженерлік есептерді моделдеу кезінде және дифференциалдық теңдеулердің шектік есептерін сандық әдістермен шешу кезінде пайда болады.
Теңдеулер жүйесі келесі түрде берілсін:
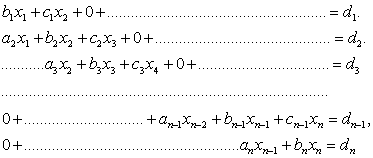
Сызықты алгебралық теңдеулер жүйесін шешудің итерациялық әдістері:
Сызықты
алгебралық теңдеулер жүйесін шешудің
жай итерациялық әдісі-![]() ;
; ![]() (2.3)
(2.3)
Алғаш ![]() векторынан
бастап, х*
нүктесіне біртіндеп жақындауды –
қарапайым итерация әдісі деп
атайды.
векторынан
бастап, х*
нүктесіне біртіндеп жақындауды –
қарапайым итерация әдісі деп
атайды. ![]() тізбегінің,
тізбегінің, ![]() кезде х*
нүктесіне жинақталуы үшін, (3.2) теңдеуіндегі
матрицалар мен векторларға шарт қою
керек.
кезде х*
нүктесіне жинақталуы үшін, (3.2) теңдеуіндегі
матрицалар мен векторларға шарт қою
керек.
Теорема 2.1.(2.3) қарапайым итерация әдісі, кез келген векторы үшін жылжымайтын х* нүктесіне жинақталуы үшін В матрицасының барлық меншікті мәндерінің модульдері бірден кіші болуы қажетті және жеткілікті.
Сызықты
алгебралық теңдеулер жүйесін шешудің
Гаусс-Зейдель әдісі-(2.2) түрдегі теңдеудің
(k+1)
қадымында, х векторының
әрбір құраушысын анықтау кезінде, оның
алында анықталған ![]() және
және ![]() құраушылары
пайдаланылады. Итерациялық теңдеу былай
жазылады:
құраушылары
пайдаланылады. Итерациялық теңдеу былай
жазылады:
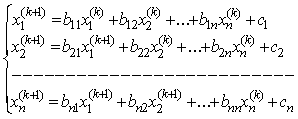 (2.9)
(2.9)
Бұл
теңдеуді матрицалық түрде жазу үшін
(2.1) теңдеуінің матрицалық түрін ![]() пайдаланайық.
Мұны
пайдаланайық.
Мұны
![]() түрде
жазып, мынандай итерациялық теңдеу
аламыз:
түрде
жазып, мынандай итерациялық теңдеу
аламыз:
![]() (2.10)
(2.10)
немесе,
![]()
(2.11)
Зейдель әдісі, (2.7) түрдегі Якоби әдісінің дербес түрі
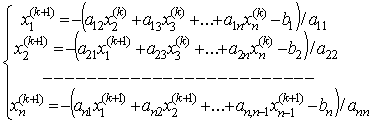
Сызықты
алгебралық теңдеулер жүйесін шешудің
Якоби әдісі-![]() теңдеуіндегі А матрицасын
теңдеуіндегі А матрицасын ![]() түрде
жазайық. Мұндағы D –
диагональ, Lжәне R,
тиісінше сол және оң жақты үшбұрышты
матрицалар. Сонда теңдеу былай жазылады:
түрде
жазайық. Мұндағы D –
диагональ, Lжәне R,
тиісінше сол және оң жақты үшбұрышты
матрицалар. Сонда теңдеу былай жазылады:
![]() .
.
Егер А матрицасының диагоналында нөлдік элемент болмаса, онда теңдеу (2.2) түріне келеді.
![]() . (2.5)
. (2.5)
мұндағы ![]() ,
, ![]() деп
алсақ, есепті қарапайым итерация әдісіне
келтіруге болады.
деп
алсақ, есепті қарапайым итерация әдісіне
келтіруге болады.
Теорема. Егер А матрицасында диагональ элементтер басым болса, Якоби әдісі жинақталады.
Сызықты алгебралық теңдеулер жүйесін шешудің Релаксация әдісі.
Егер
жоғарыдағы итерация әдістерінде,
қателіктерді бағалау үшін қажетті, В итерация
матрицасының нормасын жоғары жағынан
шектейтін ![]() ,
немесе
,
немесе ![]() сандарын
анықтау мүмкін болмаса, есептеуді қай
кезде тоқтату керектігі белгісіз
болғандықтан итерация әдісін қолдану
қиындықтар туғызады. Мұндай жағдайда,
итерациялық тізбектің жинақтылығын
тездететін, Зейдель әдісінің жалпылама
түрін қолдануға болады.
сандарын
анықтау мүмкін болмаса, есептеуді қай
кезде тоқтату керектігі белгісіз
болғандықтан итерация әдісін қолдану
қиындықтар туғызады. Мұндай жағдайда,
итерациялық тізбектің жинақтылығын
тездететін, Зейдель әдісінің жалпылама
түрін қолдануға болады.
Теңдеулер
жүйесіне Зейдель әдісін қолданған
кездегі k-жуықтау
үшін х векторының і-құраушысын ![]() деп,
ал жаңа әдіс үшін k-жуықтаудағы
құраушысын
деп,
ал жаңа әдіс үшін k-жуықтаудағы
құраушысын ![]() деп
белгілейік. Релаксация әдісін мына
формула арқылы анықтаймыз:
деп
белгілейік. Релаксация әдісін мына
формула арқылы анықтаймыз:
![]() .
.
7.Параболалық, гиперболалық, эллиптикалық және аралас типтегі механика есептері. Жылуөткізгіштік (немесе диффузия) теңдеуі, толқын теңдеуі (тасымал теңдеуі) және Гельмгольц теңдеуі. Бастапқы және шекаралық шарттарды қою. Механика есептерін аналитикалық шешудің қиындықтары.
Дербес дифференциалдық теңдеулер.
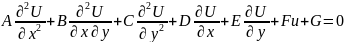 (1)
(1)
Параболалық теңдеулер.
1)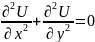 Лаплас
теңдеуі
Лаплас
теңдеуі
2)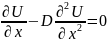 Жылуөткізгіштік d>0 немесе диффезия
теңдеуі
Жылуөткізгіштік d>0 немесе диффезия
теңдеуі
3)
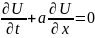 1ші ретті Толқын теңдеуі
1ші ретті Толқын теңдеуі
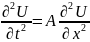 2ші
ретті Толқын теңдеуі
2ші
ретті Толқын теңдеуі
Типтерін анықтау
 гипертболалық
гипертболалық
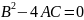 параболалық
параболалық
 эллиптикалық
эллиптикалық
(1)
Егер дебес туындылы дифференциалдық теңдеудің коэффициеннттері мынадай түрде болса теңдеулеріміздің типтері де әр түрлі болады:
1)А=1 В=0 С=1
 эллиптикалық
эллиптикалық
2)A=-d B=0 C=0
параболалық
3)
А=1 В=0 С=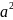
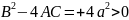 эллиптикалық
эллиптикалық
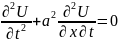
-a(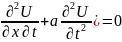
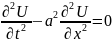
Бастапқы ж/е шекаралық шарттар
2D(Demation)
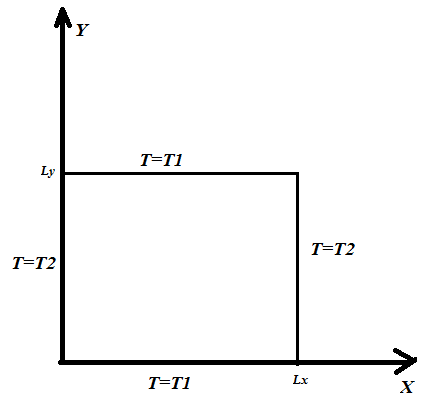
T=0
T=
X=0 T=T2
X=Lx T=T2
Y=0 T=T1
Y=Ly T=T2
Lx,Ly шекарада тұрақты мән беретін болсақ (ол Дирихле болады)
G:
T=T0(const) Дирихле шарты
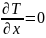 Нейман
шарты(симметриялы әдіс)
Нейман
шарты(симметриялы әдіс)
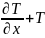 Аралас
шарт
Аралас
шарт
Шарт қою беттің физикасына тікелей байланысты болады.
