1.Бақылау мәліметтері жеткілікті болған жағдайда ең мол ағындыны есептеу. Қалыпты жылдық ағынды статистикалық қатардың кезкелген арифметикалық орташа шамасы ретінде келесі формула бойынша анықталады:

мұндағы - қалыпты жылдық ағынды, м³/с;

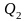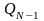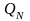, , …, , - қатардағы жылдар санының көбеюімен -нің орташа арифметикалық шамасы өзгермейтін немесе аз өзгеретін 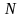ұзақ кезең ішіндегі ағындының жылдық мәндері.

Теория бойынша шамасы деректердің бас жиынтығына сәйкес келуі керек, бірақ практикада жылдық ағындыға жүргізілетін бақылау қатары ұзақтығының жеткілісіз болуына байланысты, бұл шарт орындалмайды. Бақылау бекеттерінің көбінде жүргізілген бақылау қатарларының ұзақтығы 20-30 жылдан аспайды. Сондықтан қалыпты ағындының нақты орташа мәнінен қандайда бір шамаға айырмашылығы болады. Яғни,

мұндағы - шектеулі уақыт кезеңіндегі (n жыл) орташа жылдық ағынды;

- n жыл үшін орташаланған орташа жылдық ағындының оташа квадраттық қателігі.

2.Қамтамасыздық қисығының параметрлерін моменттер әдісі бойынша бағалау. Әдістің артықшылығы мен кемшіліктері.

Вариация коэффициентін моменттер әдісі бойынша анықтау келесі формула бойынша жүзеге асырылады:

C_v=σ_Q/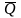 = = , (1)

мұндағы: К_і – модульдік коэффициент; – cу өтімінің жылдық мәндері; - қалыпты ағынды (ағындының көпжылдық орташа мәні);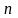 – бақылау қатарының ұзақтығы. Бірақ іс жүзінде бақылау қатарының ұзақтығы әдетте жеткіліксіз, яғни қолда бар қатар Бас жиынтық емес ұзақтығы жеткіліксіз таңдама жиынтық болғандықтан σ_Q мәні δ қателігіне ие болады. Математикалық статистикадан бұл қателіктің мынаған тең екедігі белгілі δ = және n = 30 болғанда δ шамасы δ = 1,6%, ал қатардың ұзақтығы аз болғанда ол едәуір ұлғаяды. Сондықтан бақылау қатарының ұзақтығы 30 жылдан кем болған жағдайда вариация коэффициенті келесі формула бойынша есептеледі:

C_v= . (2)

Қазіргі жағдайда бұл формула барлық жағдайда бірдей қолданылып жүр.

Вариация коэффициентін моменттер әдісімен анықтау кезінде оның кездейсоқ орташа квадраттық қателіктері төмендегідей белгіленеді:

автокорреляция есепке алынбаған жағдайда (жоқ немесе өте аз)σ_Cv = C_{v ;}

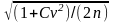автокорреляция есепке алынған жағдайда

σ_Cv= . (3)

Асимметрия коэффициенті қарастырылып отырған кездейсоқ шама қатарының өзінің орташа мәніне немесе үлестірім центіріне қатысты симметриялы еместігінің дәрежесін сипаттайды. Асимметрия коэффициенті де салыстырмалы бірлікпен өрнектеледі, бұл жекелеген өзендер қатарының немесе түрлі сипаттамалар қатарының симметриялы еместігінің дәрежесін салыстыруға, сондай-ақ тиісінше С_s коэффициентін жинақтап қорытуға мүмкіндік береді. Гидрологиялық шамалардың үлестірімі көбінесе оң ассиметриямен сипатталады. Бұл дегеніміз, бір модалы үлестірім кезінде қатардың орташа арифметикалық мәні моданың оң жағына орналасады деген сөз, демек, центрдің оң жағында үлестірім графигінің “ұзын” бөлігі орналасады. Теріс ассиметрия кезінде қатардың орташа арифметикалық мәні моданың сол жағына орналасады және үлестірімго графигінің “ұзын” бөлігі центрдің сол жағына орналасады.

Қатардың асимметриялылығын сипаттау үшін қатар мүшелерінің өздерінің орташа мәнінен ауытқуының кубының орташа мәні алынады және өлщем бірліксіз сипаттама алу үшін оны үшінші дәрежелі орташа квадраттық ауытқуға бөледі. σ=С_v болғандықтан және модульдік коэффициентін пайдаланып, (28) формуласын өрнектейміз:C_s = 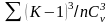. Теріс ығысуды азайту үшін δ түзетуі енгізіледі. δ = n² /(n-1)(n-2) болғанда (29) формула келесі түрге ие болады:

С_s=n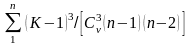 . Асимметрия коэффициентінің мәні оң немесе теріс болуы мүмкін. Оң 0ассиметрия суы аз жылдарға қарағанда суы мол жылдар сирек қайталанған жағдайда байқалады, яғни қатардың орташа мәніне кіші мәндері жиі кездеседі. Керісінше болғанда қатар теріс ассиметрияға ие болады. Асимметрия коэффициентінің орташа квадраттық қателігін Крицкий-Менкел формуласымен анықтауға болады.

σ_Cs = 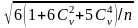₁₀₀.

емек, асимметрия коэффициентінің қателігі қатардың ұзақтығы қысқарған сайын және вариация коэффициентінің мәні кіші болғанда ұлғаяды.

Есептеулер С_v-ның кез келген мәнінде және n<50 болғанда асимметрия коэффициентінің қателігі ондаған тіпті жүздеген процентті құрайтынын көрсетеді. Сондықтан іс жүзінде C_s коэффициентін С_v коэффициентіне қатынасы арқылы (C_s/C_v) эмпирикалық нүктелерге сәйкес келетін теориялық қамтамасыздық қисығын таңдау әдісін пайдаланып анықтайды. Есептік қатынас ретінде қисықтың түзуленуі жүзеге асатын немесе эмпирикалық нүктелердің орналасуына аналитикалық қисық барынша сәйкес келетін қатынас қабылданады.