19. Коэффициенты эластичности для ряда математических функций:

20. Общее понятие о системах линейных уравнений, используемых в эконометрике. Структурная и приведенная форма модели.

Если экономический процесс не поддаётся описанию посредством одной модели регрессии, то в подобных ситуациях прибегают к построению нескольких эконометрических уравнений, которые в совокупности образуют систему.

В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных (у) и множество предопределённых переменных (лаговые (– за предыдущий период) и текущие независимые переменные, а также лаговые эндогенные переменные).

Системы эконометрических уравнений используются для объяснения текущих значений эндогенных переменных в зависимости от значений предопределённых переменных.

Системы эконометрических уравнений, которые используются в эконометрическом моделировании, подразделяются натри типа.

1. Система независимых эконометрических уравнений - это система, где каждая зависимая переменная рассматривается как функция одного и того же набора факторов или х.

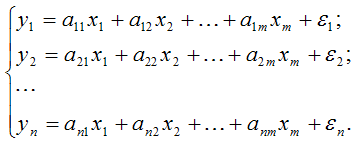
2. Система рекурсивных эконометрических уравнений – зависимая переменная у одного уравнения выступает в качестве фактора х в другом уравнении.

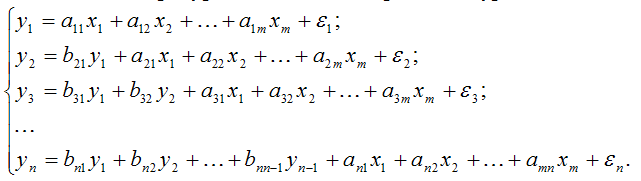
3. Система взаимозависимых эконометрических уравнений

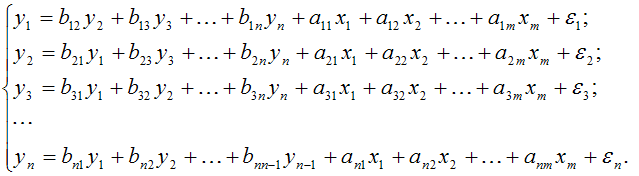
Данная система характеризуется тем, что эндогенные переменные в одних уравнениях входят в левую часть (т. е. являются результативными переменными), а в других уравнениях – в правую часть (т. е. являются факторными переменными).

Коэффициентов этих уравнений можно рассчитать с помощью классического метода наименьших квадратов.

Структурными уравнениями называются уравнения, из которых состоит исходная система одновременных уравнений. В данном случае система имеет структурную форму.

Структурная форма системы одновременных уравнений непосредственно характеризует реальный экономический процесс.

Структурными коэффициентами или параметрами называются коэффициенты уравнений структурной формы системы одновременных уравнений.

Структурные уравнения могут быть представлены либо поведенческими уравнениями, либо уравнениями-тождествами

Приведённой формой системы одновременных уравнений называется система независимых уравнений, в которой все эндогенные переменные выражены только через экзогенные или предопределённые переменные и случайные компоненты, например:

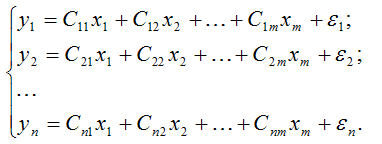
Приведёнными коэффициентами или параметрам называются коэффициенты приведённой формы системы одновременных уравнений.

Оценки неизвестных приведённых коэффициентов можно рассчитать с помощью классического метода наименьших квадратов, а уже на их основе определить оценки структурных коэффициентов.

При переходе от структурной формы системы одновременных уравнений к приведённой форме может возникнуть проблема идентификации модели.

21. Проблема идентификации

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Индетификация - это единственность соответствия между приведенной и структурной формами модели.

С позиции идентификацируемости структурные модели можно подразделить на три вида:

· идентифицируемые;

· неидентифицируемые;

· сверхидентифицируемые.

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной модели, т.е. если число параметров структурной модели равно числу параметров приведенной формы модели.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверить на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо.

Необходимое условие: чтобы уравнение было идентифицируемо, необходимо, чтобы число экзогенных переменных (D), отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении (H) без одного.

D+1=H - уравнение идентифицируемо;

D+1<H - уравнение неидентифицируемо;

D+1>H - уравнение сверхидентифицируемо.

Достаточное условие: уравнение идентифицируемо, если по отсутствующим в нем экзогенным и эндогенным переменным можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.