12. Применение парной линейной регрессии при изучении функции потребления
Парная линейная регрессия используется в эконометрике нередко при изучении функции потребления. Cтатистическая модель Кейнса для описания народного хозяйства страны в простом варианте имеет следующий вид:
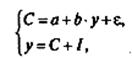
где С – личное потребление в постоянных ценах,
у – национальный доход в постоянных ценах;
I – инвестиции;
- случайная величина.
Коэффициент b не может быть больше 1. Он характеризует предельную склонность к потреблению. Если он равен, например, 0,65, то из каждой дополнительной тысячи дохода на потребление расходуется в среднем 650 руб., и 350руб. инвестируется, т.е. С и у выражены в тыс.руб. Если b>1, то y<C+I, т.е. на потребление расходуются не только доходы, но и сбережения.
Параметр а Кейнс истолковал как прирост потребления за счет др. факторов.
Структурный коэффициент b используется для расчета мультипликаторов. По данной функции потребления можно определить 2 мультипликатора – инвестиционный мультипликатор потребления Mc=b/(1-b) и инвестиционный мультипликатор национального дохода – My=1/(1-b).
Пример: Mc=0,65/(1-0,65); My=1/(1-0,65) 1) Mc- эта величина означает, что дополнительные вложения в размере 1 тыс.руб. приведут при прочих равных условиях к дополнительному увеличению потребления на 1,857 тыс.руб. 2)My- доп.инвестиции в размере 1 тыс.руб. на длительный срок приведут при прочих равных условиях к дополнительному национальному доходу в 2,857 тыс.руб.
Модель Кейнса точно идентифицируема, и для получения величины структурного коэффициента b используется КМНК.
13. Нелинейная регрессия. Классы нелинейных регрессий.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются соответствующими нелинейными функциями.
Нелинейные регрессии делятся на два типа:
Регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам. Примером может служить гипербола (y=a+b/x+ε) и полиномы различных степеней (у=а+b1x+b2x2+b3x3+ε). Для оценки параметров можно использовать МНК, так как эти функции линейны по параметрам. Полином любой степени сводится к линейной регрессии с её методом оценивания. А в гиперболе МНК можно использовать после замены переменной 1/x=z.
Регрессии, нелинейные по оцениваемым параметрам: степенная (y=axb), показательная (y=abx), экспоненциальная (y=ea+bx). Непосредственное применение МНК невозможно. Функции необходимо приводить к линейному виду, путём логарифмирования.
14. Системы нормальных уравнений для нелинейных моделей регрессии
Рассмотрим
применение МНК для случая полинома
второго порядка. Применение МНК для
оценки параметров второй степени
приводит к следующей системе нормальных
уравнений:
Решить её можно методом определителя (Крамера): а=Δа/Δ; b=Δb/Δ; c=Δc/Δ.
Δ – определитель системы; Δа, Δb, Δс – определители, полученные заменой соответствующего столбца на столбец свободных членов.
С помощью замены z=1/x, для равносторонней гиперболы получим уравнение регрессии y=a+bz, для оценки параметров которого применим МНК и получим следующую систему нормальных уравнений:
При b>0 имеем обратную зависимость, которая при x→∞, характеризуется минимальным значением Y, оценкой которого является a. При b<0 имеем медленно повышающуюся функцию с верхней асимптотой а при x→∞.
Рассмотрим теперь модели нелинейные по оцениваемым параметрам. Эти модели подразделяются на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований (логарифмирования обеих частей уравнения) может быть приведена к линейному виду, тогда можно использовать МНК. Если нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции.