8. Модель парной линейной регрессии
Если функция регрессии линейна, то говорят о линейной регрессии. Модель линейной регрессии (линейное уравнение) является наиболее простым и распространённым видом зависимости между экономическими переменными.
Y=a+bx+ε
У – зависимая переменная;
X – переменная, объясняющая значение зависимой переменной; ε – ошибка;
A и b – коэффициенты уравнения. Причем коэффициент а (свободный член регрессии) показывает величину Y при нулевом X, т.е. если значение объясняющей переменной (Х) будет равно 0, то значение объясняемой переменной (У) будет равно а. Коэффициент b (угловой коэффициент) фактически показывает, на сколько единиц в среднем изменится значение Y при изменении Х на одну единицу. Если коэффициент b – отрицательный, то с ростом Х, У будет уменьшаться; а если b>0, то с ростом Х, У будет увеличиваться.
Допустим, что нашей задачей является подбор функции Y=F(x), наилучшим способом описывающей зависимость Y от Х. У нас есть три метода выбора этой функции:
Графический способ (перенесение данных в систему координат)
Аналитический
Экспериментальный
9. Метод наименьших квадратов. Вывод для нахождения параметров уравнений регрессии
При использовании МНК, параметры а и b выбираются таким образом, чтобы сумма квадратов отклонений теоретических значений от фактических было бы минимальным. Найденные значения параметров, которые минимизируют указанную сумму квадратов разностей, называются оценками неизвестных параметров по методу наименьших квадратов. Полученные оценки подставляются в функцию f(x) вместо неизвестных коэффициентов. В результате после подстановки получается функциональная зависимость, в которой нет неизвестных параметров.
Основные особенности МНК:
1) Он наиболее простой с вычислительной точки зрения.
2) Оценки коэффициентов регрессии по МНК
обладают рядом оптимальных свойств
Вывод уравнений:
(вместо RSS пишите просто S)
Находим минимум функции:
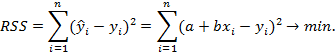
Находим производную:
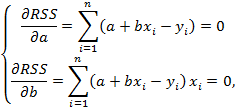
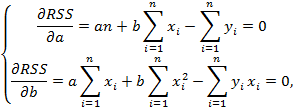
Делим на n, получается:
(y
с палочкой и х с палочкой – средние
значения)
Решив
полученную систему относительно
неизвестных параметров
,
получим:
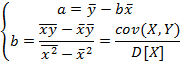(вместо
D(X)
пишите S2x)
10. Мнк, геометрическая интерпретация
Например, мы имеем линейную зависимость между площадью квартиры (Х) и её стоимостью (У). Тогда график МНК будет выглядеть так:
Точки – это значения, которые нам были даны по условию, т.е. фактические значения. А прямая – это теоретические значения. Суть МНК в том, чтобы квадраты расстояний между этими точками и прямой были минимальны.
11. Коэффициент корреляции
Тесноту ( силу ) связи изучаемых показателей оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.
Если коэффициент корреляции > 0,7 - связь между показателями сильная
Если 0,3 < коэффициент корреляции < 0,7 - связь между показателями умеренная
Если коэффициент корреляции < 0,3 - связь слабая.
Фактически он показывает, как сильно изменится У, если изменится У.
Формулы вычисления коэффициента корреляции для линейной регрессии:
=
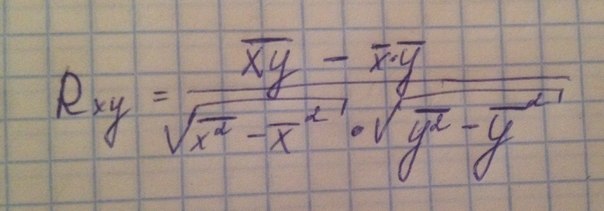
Формула коэффициента корреляции для нелинейной регрессии:
