1. Многоугольник — это геометрическая фигура, ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех и более отрезков (звеньев).

Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. 

Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины.

Сумма углов выпуклого n-угольника равна 180°•(n - 2) градусов.

2. Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.

Теоремы (свойства параллелограмма):

• В параллелограмме противоположные стороны равны и противоположные углы равны: ,  ,  , .

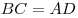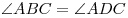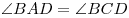• Диагонали параллелограмма точкой пересечения делятся пополам:  ,  .

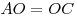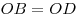• Углы, прилежащие к любой стороне, в сумме равны  .

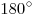• Диагонали параллелограмма делят его на два равных треугольника.

• Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:  .

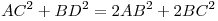Признаки параллелограмма:

• Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

• Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника   являются вершинами параллелограмма Вариньона.

• Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника 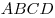 . Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.

3. Трапецией называется четырехугольник, у которого одна пара параллельных сторон.

Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Свойства трапеции

• ее средняя линия параллельна основаниям и равна их полусумме;

• если трапеция равнобокая, то ее диагонали равны и углы при основании равны;

• если трапеция равнобокая, то около нее можно описать окружность;

• если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне

4. Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства прямоугольника

• все свойства параллелограмма;

• диагонали равны.

Признаки прямоугольника

Параллелограмм является прямоугольником, если:

1. Один из его углов прямой.

2. Его диагонали равны.

5. Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба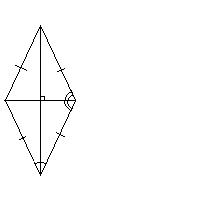

• все свойства параллелограмма;

• диагонали перпендикулярны;

• диагонали являются биссектрисами его углов.

Признаки ромба

1. Параллелограмм является ромбом, если:

2. Две его смежные стороны равны.

3. Его диагонали перпендикулярны.

4. Одна из диагоналей является биссектрисой его угла.

Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства квадрата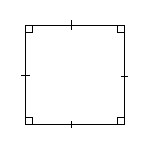

• все углы квадрата прямые;

• диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Признаки квадрата

Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

S	=	1	d1d2
		2

S	=	4r2
		sinα

7.Ромб: S = ah S = a² sinα

S = 2ar

Параллелограмм:

S = ah_a

S = ab sin 

S = d₁d₂ sin 

6. Площади фигур – это размеры части плоскости, занимаемой этими фигурами, выраженные в определенных единицах. 

1. Трапеция a и b — основания; h — расстояние между ними; l — средняя линия.

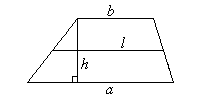
S = lh

1. Прямоугольник

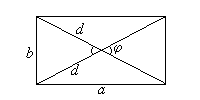
S = ab

S = d₁d₂ sin 

1. Квадрат d — диагональ.

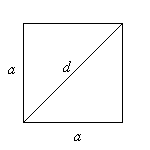
S = a²

S = d²

8. Формулы площади треугольника

1. Произвольный треугольник

a, b, c — стороны;   — угол между сторонами a и b; — полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; h_a — высота, проведенная к стороне a.

S =  ah_a

S =  ab sin 

S = pr

2. Прямоугольный треугольник

a, b — катеты; c — гипотенуза; h_c — высота, проведенная к стороне c.

S =  ab

S =  ch_c

3. Равносторонний треугольник

Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.

9. Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)

Свойства прямоугольного треугольника

• Сумма двух острых углов прямоугольного треугольника равна 90º

Сумма углов треугольника равна 180º, а прямой угол равен 90º, поэтому сумма двух острых углов прямоугольного треугольника равна 90º.

• Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы.

• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º.

Теорема Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Верна и теорема, обратная П. т.: если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то этот треугольник прямоугольный.

10. Подобие плоских фигур. Если изменить ( увеличить или уменьшить ) все размеры плоской фигуры в одно и то же число раз ( отношение подобия ), то старая и новая фигуры называются подобными

Признаки подобия треугольников.

1) Признак подобия треугольников по двум углам:

- если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Признак подобия треугольников по двум сторонам и углу между ними:

 - если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.

3) Признак подобия треугольников по трем сторонам:

- если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

 

Подобие прямоугольных треугольников.

Если один из острых углов прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу