§ 2.2.4 Бағдарламалаудың басқа тілдері және жүйелері.

Ғалымдардың жаңа бағдарламалық жүйелер құрастыру туралы ой-пікірлері үнемі көп және әр-түрлі болып келді. Бір пікірлер компьютерлердің архитектурасы ерекшеліктеріне басқалары математиканың немесе теориялық бағдарламаның әртүрлі тарауларына негізделді. Мысал ретінде, Sisal, Haskel, Cilk, T-система, НОРМА және т.б. жүйелерді атауға болады. Ондай жүйелер көп. Бірақ жүйелердің нақты таралуын негізінен үш фактор айқындайтыны белгілі: бағдарламалаудың қарапайымдылығы, бағдарламаның тиімділігі, жеңіл тасымалдануы. Ия, бірақ осы талаптарға толық жауап бере алатын бағдарламалық жүйе құру есебі әлі де шешілген жоқ. Сондықтан да, жаңа жүйелер құрудың базасы болатын ой-пікірлердің қаншалықты қызықты болатынын қарастырып көрелік.

Осы параграфта біз россиялық екі жүйе туралы қысқаша айтатын боламыз: Т-жүйесі және НОРМА тілі [10]. Бұл жүйелеудің біреуі бағдарламаны автоматты динамикалық параллельдеуге, ал екіншісі математикалық формулалар терминдері арқылы бағдарламалауға мүмкіндік береді.

Т- жүйесі

Т-жүйесін құру өткен ғасырдың 80-ші жылдарының соңында РҒА (РАН)-ның бағдарламалық жүйелер Институтында басталған болатын.

Т-жүйесіне тән негізгі ерекшелік: бағдарламаларды динамикалық параллельдеуді қамтамасыз ету үшін функционалды бағдарламалау парадигмасын пайдалану болып табылады. Осының негізінде параллель есептеуді ұйымдастыру үшін Т-жүйесінде қызықты формаларды жүзеге асыруға және де табуға мүмкіндік туды. Мысалға алсақ, жүктемені бөлу немесе синхрондау үшін. Сонымен қатар, Т-жүйесінің функционалды стилін С, С++ тілдерінің кеңейтілуі немесе Fortran тілі көмегімен дәстүрлі бағдарламалау тілдерімен бірге тиімді пайдалану мүмкіндігі туды. Бұл тілде нақты параллельді конструкция жоқ және де бағдарламашы мәтінде бағдарламаның қай бөліктерін параллель орындау керек екенін анық көрсетпейді.

Т-жүйесінің базалық қағидалары функционалды бағдарламалаудың жалпы теориясының нәтижелеріне негізделген. Оны айқындау, түсіндіру үшін теорияның әрбір бөлігіне мән бермей-ақ сол сияқты жай теорияларды, яғни қарапайым аналогтарын пайдалануға болады. Мысалға, бір күрделі арифметикалық өрнек бар болып, оған өз кезегінде көптеген жақшаға алынған өрнекшелер кірсін делік. Әрине, бұл есептің шешімін кезкелген тәртіппен шешуге болады және әр жағдайда да нәтижесі бірдей болады. Функционалды бағдарлама теориясында арифметиканың бұл заңы еркін рекурсивті функцияларға да жалпыланады.

Бұндай тәсіл бізге «таза» функциялардан құрылған функционалды бағдарламаларды параллельдеу үшін тіке әдісті береді. Таза функциялар дегеніміз қосалқы әсерсіз функцияларды білдіретін Т-жүйенің базалық ұғымдарының бірі болып табылады. Әрбір уақыт мезетінде есептеуге дайын «өрнекшелерді» белгілеп алып, оларды пайдаланудағы процессорларға бөліп беру керек. Бұл жерде негізі ретінде, түйіндері -шақырылған функцияларды көрсететін, ал доғалары - «өрнекше-өрнек» қатынасына сәйкес келетін граф алынады.

Дәстүрлі бағдарламалау тіліне функционалды семантиканы қосу үшін, «дайын емес мән» ұғымын енгізу жеткілікті болады екен. Бұл С тілінде айнымалыларды сипаттауда қосымша атрибутты енгізу арқылы жүзеге асырылады. Жаңа tval кілттік сөзі «tval int i» сипаттауында мәні бүтін немесе дайын емес мән болатын айнымалыны анықтайды. Қосалқы әсерсіз функцияларды белгілеу үшін қосымша tfun сөзін қолданады. Шығу Т - функциясы tout сөзімен белгіленеді. және т.б.

Қарапайым мысал қарастырайық :

tfun void tmain(...) {

tval int x, у, z, b = 1;

int w, t, a = 5;

G(a, b, &x, &y, &z); /* x, у, z –те нәтижелерді қабылдау*/

b = z;

У = a;

w = a;

t = b+a*w;

…

}

Берілген G функциясы таза және онда tfun атрибуты бар деп есептейік. Мысалды «қадам» бойынша орындаймыз.

1. G (a, b, &x, &y, &z ). G функциясы таза болғандықтан ол негізгі бағдарламамен параллель орындалуы мүмкін. Осы оператор орындалғаннан кейін Т-жүйесі G-функциясының шақырылуының негізінде, параллель орындалуға дайын жаңа жұмыс үлесін рәсімдейді.

Бұл жұмыс үлесі тез арада орындалуы да, немесе басқа себептер болып оның орындалуы кейінге қалдырылуы да мүмкін. Қай жағдайда да жүйе келесі операторды орындауға көшеді. Айнымалылар x, y, z - дайын емес айнымалылар статусын алады және дайын емес мәндерді қабылдайды.

2. b = z. Енді b айнымалысы да дайын емес болды, ал жүйе ешқандай бөгеліссіз одан ары бағдарламаны орындайды. Бұл мысал, дайын емес мәндерді көшіруге болатынын көрсетеді. Бірмезетте біз G функциясы нәтижесінің тұтынушылар құрамын да өзгерттік. Енді үшінші нәтиже Z айнымалысына да, дәл осылай B айнымалысына да берілуі тиіс. Әрине, осы мезеттегі b айнымалысының дайын емес екендігі, G функциясының аргументі ретінде алынған b мәніне еш әсер етпейтінін байқаймыз.

3. y = a. Айнымалы а - жай, сондықтан дайын емес y айнымалысы дайын болады және де а айнымалысының мәнін қабылдайды.

4. w = a. Бұл оператордың орындалуында қиыншылық туындамайды, себебі мұнда жай айнымалылар пайдаланылған.

5. t=b+a*w. Бұл операторда фрагменттің орындалуы, қашан G функциясы b айнымалысының нәтижесін қайтармайынша бұғаттауда болады. Екінші оператордағыдай, мұнда дайын емес мәндерді көшіруге болады, бірақ олармен ешқандай басқа операциялар орындауға болмайды.

Бұл фрагментке қатысты анықталмаған бір сұрақ қалады. Үшінші оператор үшін, фрагмент детерминделген құлығына ие болмайды деген әсер туындауы мүмкін. Шынында , егер «y = a» операторы G функциясының аяқталуынан ерте орындалса, онда y айнымалысының мәні G функциясымен анықталады, ал егер кеш орындалса онда у айнымалысы а мәнін қабылдайды. Негізінде детерминделу қамтамасыз етілген. Осы оператор орындалғаннан кейін у айнымалысының мәні әрқашан а мәніне тең болады. «y = a» операторын өңдеу алдында у айнымалысы бұғатталады.

Бұдан әрі айнымалының мәнін тексеру орындалады, егер мәні дайын емес болса, онда күтілетін мәнді қабыл алмау ұсынылады және жабдықтаушымен байланыс үзіледі. Біздің жағдайда бұл қабылдамау G функциясының орындалуынан шығатын мән. Барлық тексерістерден және оператордың орындалуынан кейін айнымалы бұғаттаудан босатылады. Мұндай тізбек бағдарлама құлығының детерминделгенінің кепілін бере алады және де әдеттегідей семантиканы қамтамасыз етеді: y = a орындалғаннан кейін у мәні а мәніне тең болады.

Жаңа кілттік сөздер қосылғаннан кейінгі С тілінің диалекті, ТС деп аталады. Жаңа тіл көптеген бағдарламалаушыларға бағдарламаларды функционалды стильде жазу үшін әдеттегідей императивті жазбаны қолдануға мүмкіндік береді.

Т-жүйесінің және ТС тілінің базалық конструкцияларымен танысу үшін екі қарапайым мысал қарастырайық: Фибоначчи санының есептелуі және ағаш тәрізді деректер структурасын рекурсивті қарап шығу.

Фибоначчидің n- ші санын табу есебін қарастырайық:

Т- жүйесін қолдана отырып есепті шешу бағдарламасының мәтіні төменде көрсетілген. Жолдардың нөмірі, әрине Т-жүйесінің бөлігі болмайды. Олар бізге бұдан әрі бағдарламалардың әртүрлі конструкцияларына түсінік бергенде керек болады.

001 # include <tc.h>

002

003 # include <stdio.h >

004 # include <stdlib.h >

005

007 unsigned cfib (unsigned _n)

008 {

009 return _n < 2 ? _n : cfib (_n-1) + cfib (_n-2)

010 }

011

012 tfun viod fib (unsigned _n, tout unsigned *_res)

013{

014 if (_n <32) {

015 *_res = cfib(_n)

016 } else {

017 tval unsigned res1, res2;

018 fib (_n-1, &res1);

019 fib (_n-2, &res2);

020 *_res = res1+res2;

021 }

022 }

023

024 int tmain (int argc, char* argv[])

025 {

026 unsigned n;

027 tval unsigned res;

028 if (argc < 2) {

029 terrprint (

030 “Usage:\n”

031 “ gr_fib <number>\n”

032 );

033 return - 1

034 }

035 n= (unsigned)atoi(argv[1]);

036 fib(n, &res);

037 (unsigned) res;

038 terrprint(“fib(%u) = %u\n”, n, rez)

039 return 0;

040 }

Бағдарламада tval кілттік сөзі көмегімен жай және дайын емес мәндерді сақтай алатын res1, res2 және res айнымалылары анықталған.

Олардың адрестері fib Т-функциясына берілген мезетте, ал ол 18,19 және 36 жолдардағы fib шақыруы, шақыру функциясының орындалуы тоқтамайды және ол ары қарай жұмысын жалғастырады. fib екінші формальды параметрінің сипатталуы tout болғандығы себепті шақырулар мезеттерінде сәйкес айнымалы res1, res2 және res «дайын емес» болады. Ол дәл сол арнайы дайын емес (даярлықсыз) мәнді қамтиды. Қашан шақырылған функция fib нәтижені есептейді және оны айнымалыға қайтарады (жол 15 болмаса 20), бұл мән жай «дайын» мәнімен алмастырылады.

«Дайын емес» айнымалыларға қатынас (олардың мәндеріне) функцияның есептеу процесін бұғаттайды. Мысалы, ол 20 –шы жолда болуы мүмкін, онда res1 және res2 айнымалыларына қатынас (обращение) тұр. 18-ші және 19-шы жолдарда res1 және res2 айнымалыларының мәндерін білу қажет етілмейді, сондықтан fib Т-функциясының екі шақыруы да бұғаттаусыз орындалатын болады, және олары есептеу параллельді жүруі мүмкін.

Бағдарлама жұмысы барысында туындаған Т-функциясы fib шақырулары (18, 19 және 36 жолдар) есептеуге дайын тәуелсіз жұмыс порцияларын қалыптастырады (параллельділік гранулалары). Барлық бөліктер (порциялар) кезекке қойылады, олардан есептеуіш орындаушы - процестер өздері үшін жұмыс алады. Бағдарламаның мәтінінде Т-функциялары кодтың потенциалды параллель фрагменттерінің үлгілерін көрсетеді. Бағдарламаның жұмысы барысында Т-функциясы нақты шақыруының нәтижесі сияқты нақты параллельді фрагменттер пайда болады және Т-жүйесімен өңделеді.

Бағдарламада 14 жолда тұрған шартты оператор 2 есепті орындайды. Бір жағынан, қандай да бір уақыт мезетінде жаңа жұмыс порцияларының құрылуын тоқтату, және соңғы қорытынды нәтижені қалыптастыруды бастау керек. Бұл мағынада мұнда жай рекурсивті функциялармен толық ұқсастық бар. Басқа жағынан, барлық қалыптасқан жұмыс бөліктері жеткілікті салмақты болулары тиіс. Кезекті бөліктің қандай да бір процеске берілуі есебінен болатын қосымша шығындарды жасыру керек, оны есептеу көлемін арттыру арқылы істеуге болады. Осы ойлардан келіп берілген жолдағы 32 тұрақтысы пайда болады.

Дегенмен, дайын емес айнымалылар Т-жүйесінде синхрондаудың негізгі құралы болады. Дайын емес айнымалыларды оқу (мәнге қатынас) және жазу (қабылдау үшін қатынас) жағдайларының, яғни ситуацияларының айтарлықтай айырмашылықтары бар:

• дайын емес айнымалы оқу барысында осындай қатынасты орындайтын есептеу процесін бұғаттау орын алады; оның күтуі, айнымалы дайын мәнді алғанға дейін жалғасады;

• жай мәнді дайын емес айнымалыға жазу барысында ол өзінің тұтынушылары үшін дайын болады, ал берілген айнымалыда ертеректе (алдында) бұғатталған процестер бұғаттау жағдайынан шығады.

Енді қашықтағы көрсеткіштермен жұмысты суреттейтін ағашты рекурсивті аралап шығу бағдарламасын қарастырайық.

001 # include <tc.h>

002

003 # include <stio.h>

004 # include <stlib.n>

005

006 struct tree {

007 struct tree tptr ieft;

008 struct tree tptr right;

009 int value;

010 };

011

012 struct tree tptr create_tree (int deep) {

013 struct tree tptr res = tnew ( struct tree);

014 res ->value = 1;

015 if (deep <=1) {

016 res ->left = NULL;

017 res ->right = NULL;

018 } else {

019 res ->left = create_tree(deep – 1);

020 res ->right = create_tree(deep – 1);

021 }

022 tvalidate (*res);

023 return res;

024}

025 tfun void tsum (cost struct tree tptr _ tree,

026 tout int *_res) {

027 tval int left_sum, right_sum;

028

029 if (_tree->left ! = NULL) {

030 tsum (_tree->left, &right _sum);

031 } else {

032 left_sum = _tree->value;

033 }

034 tsum(_tree->right, &right_sum);

036 } else {

037 right_ sum = _tree->value;

038 }

039 *_res = left_sum + right_sum;

040 }

041

042 int tmain (int argc, cgar* argv [])

043 {

044 struct tree tptr tree = create_tree(12);

045 tval int sum;

046 tsum (tree, &sum);

047 terrprint (“sum = %u\n”, sum);

048 return 0;

049 }

Бұл бағдарламада tree типтегі құрылым ағашы алдымен create_tree функциясымен туындайды, одан кейін tsum рекурсивті функциясында араланады. Алдыңғы мысалдағы сияқты ағаштың әрбір түйінінде параллельдеу жүргізіледі: алдымен бұтақтың оң және сол жақ тармақтарында шақырулар пайда болады, содан кейін ғана аралау нәтижелеріне қатынас жасалады.

Негізгі сөз (кілттік сөз) tptr дайын емес айнымалыларға жасалған ауқымды сілтемелерді суреттеу үшін қызмет етеді. Жазу операциясы кезінде мән жүйенің керекті торабына беріледі, онда ол мән сәйкес Т-айнымалыға жазылады және оны дайын етеді.

Т-жүйесін пайдалану тәжірибесі ТС тілінде бағдарламаны құрастыру процесінде келесі қадамдар тізбегін ұсынады:

1. Кодтың дизайнын құрастыру. Бұл этапта мына сұрақтар шешіледі: қандай алгоритм фрагменттері ТС-тілінде Т-функциясы түрінде іске асырылады, ал қандай фрагменттер үйреншікті тізбекті орындалатын код түрінде C, C++ немесе Fortran стандартты тізбекті бағдарламалау тілдерінде іске асырылған.

2. Бір процессорлық компьютерде орындау және алғашқы жөндеу. Құрастырылған ТС-бағдарлама дәстүрлі қарапайым бір процессорлық компьютерде тізбекті режимде Т-жүйесін қолданбай жөнделеді. Ол үшін С тіліне қосылған барлық жаңа кілттік сөздер автоматты түрде сәйкес макростар (мысалы: tptr сөзі - “*”: tval - “бос“ және т.б.) көмегімен қайта анықталады.

3. Көп процессорлы құрылғыларда жөндеу. ТС-бағдарламасын бір процессорлы компьютерде тізбекті режимде жөндеуден кейін, параллельді есептеу ортасында толық функционалды жөндеу жүргізіледі.

4. Тиімділеу. Соңғы этапта, трассировка, профилировка және басқа да құрылғылар көмегімен кезкелген параллель бағдарламалау технологиясына тән бағдарламаны тиімділеу процесі жүргізіледі.

Басқа параллель бағдарламалау жүйесімен салыстырғанда Т-жүйесінің артықшылығы екі жағдайда анық білінеді. Бірінші жағдай, бағдарламаны орындауға дейін параллель процесстердің жұмысын қалай реттеу туралы дәл ақпараттың болмауы. Екінші жағдай, бағдарламаны есептеу схемасы функционалды модельге жақын және бір-бірін рекурсивті шақыратын функциялар жиынының көмегімен тиімді көрсетілуі мүмкін кездерде пайда болады. Т-жүйесінің күшті жағының бірі, ол бағдарламашыны параллель бағдарламалауға тән көптеген дәстүрлі әркеттерден босатады: бағдарламаның параллель фрагменттерін айқын ұйымдастыру, оларды кластер тораптарына тарату, фрагменттер жұмысын синхрондау, олардың арасында бір-бірімен мәлімет алмасудың айқын операцияларын орындау.

Т-жүйесінің кемшіліктеріне де тоқтала кетейік. Негізінен, ол кемшіліктер жайында айқын түрде айтыла бермейді, бірақ олар туралы білу керек екені түсінікті. Типтік мысал – деректерді кластердің бір торабынан екінші торабына жіберетін Т-функциясының шақыруы. Сырттай қарағанда ешқандай күмәнді нәрсе жоқ, ал қосымша шығындар өте үлкен болуы мүмкін. Егер бағдарламаны жобалау барысында бұл факторды ескермесе, онда оның тиімділігі жағынан үлкен проблемалар туындауы мүмкін. Жүйе тиімділікке кепілдік бере алмайды. Мұнда да, Т-жүйесі үшін бағдарламаны іске асыру кезінде бағдарламашы алгоритмді функционалды түрде мазмұндап және бағдарламаны таза Т-функцияларының жиыны түрінде сипаттауға міндетті. Бұны ыңғайсыз деуге болмайды, бірақ ол әдеттегіден тыс және мұнда бағдарламашыға потенциалды параллель фрагменттердің тімді өлшемін де таңдау керек болады. Т-функциясының өте кіші есептеу күрделілігі көп мөлшердегі қосымша шығындарға әкелуі мүмкін. Өте үлкен есептеу күрделілігі (қиындықтары) параллель фрагменттердің аз туындауына, ол өз кезегінде жүйе есептеу тораптарының бірқалыпсыз жүктелуіне әкелуі мүмкін.

НОРМА бағдарламалау жүйесі.

НОРМА тілі мамандандырылған процедуралық емес тіл болып табылады. Ол негізінен есептеуіш сипатындағы мәселелерді шешуге, дербес жағдайда математикалық физика есептерін шешуге арналған десе болады. Тілдің барлық конструкциялары декларативті сипатта және мәндерді есептеу ережесін суреттейді. Тілдің негізгі тағайындалуы бағдарламаны құрастыру процесін автоматтандыру болып табылады. Бағдарламашы мұнда негізінен математикалық формулалар терминінде жұмыс істегендіктен, ол өз кезегінде оның жұмысын айтарлықтай жеңілдетеді және ықшамдайды. Транслятордың жұмысы күрделенеді. Дәстүрлі мәселелермен қатар, мысалы, дербес жағдайда синтаксистік және семантикалық талдау, ол шығыс бағдарламасының синтезін орындайды.

Берілген есептің спецификациясына сәйкес бағдарламаны автоматты түрде құруға мүмкіндік беретін идеялар, 1963 жылы И. Б. Задыхайлоның жұмысында [21] келтірілген. Ол идеялардың одан ары дамуы НОРМА тілінің және әртүрлі платформалар үшін транслятордың бірнеше нұсқауының пайда болуына әкелді.

Алғашында НОРМА термині (Непроцедурное Описание Разностных Моделей Алгоритмов) алгоритмдердің айырымдық модельдерінің процедуралық емес сипаттамасы деп таратылып айтылды. Соңынан басқа трактовка пайда болды: – (НОРМАльный уровень общения прикладного математика с компьютером) қолданбалы математиктің компьютермен қатысының НОРМАльды деңгейі. Қолданбалы бағдарламаны құрастырушы, нақты компьютердің ерекшеліктерін негізге ала отырып, өз пәндік облысының үйреншікті терминінде ойлайды. РҒА (РАН) В. М. Келдыш атындағы қолданбалы математика институтының нақты қажеттіліктерін ескере отырып, тілдің авторлары математикалық физика мәселелерін шешуді барынша (максималды) ықшамдауға тырысты. Пәндік облыс спецификасы - бұл торлық тәсілдерді негізге алу, соларға бағытталу.

НОРМА тіліндегі бағдарлама жазбасы операцияның орындалу реті туралы ешқандай мәліметті қажет етпейді. Тіл сөйлемдерінің реті еркін болуы мүмкін. Есептеулерді қалай ұйымдастыру керек екенін түсіндірмей ақ, бұл тілде есептеулерге сұраныс жасау мүмкіндіктері қарастырылған. Барлық ақпараттық байланыстар, берілген бағдарламаны талдау және шығатын тексті синтездеу этапында транслятор–синтезатормен анықталады және ескеріледі.

Есептеулерді ұйымдастырудың нақты тәсілін таңдау трансляторға жүктеледі. Дербес жағдайда, мысалы, қорытынды бағдарламаны синтездеу этапында, ол тізбекті кодты да, параллель кодты да генерациялай алады.

НОРМА тілінің жоғары деңгейін таңдау оның өзіне тән сипатын анықтайды – бұл айнымалыны бір реттік меншіктеу тілі. Мұнда әрбір айнымалы өзіне бір рет қана мән қабылдай алады және жады, қосымша әсер, меншіктеу операторы және басқарушы операторлар сияқты түсініктер НОРМА тілінде «анықтама бойынша» жоқ. Барлық дәстүрлі бағдарламалау тілдерінде бұл түсініктер бар, себебі олардың көмегімен үнемділік, жадының таратылуы, операторлардың орындалу ретін анықтау және т.б. сұрақтарды ескере отырып нақты алгоритм құру керек болады. Негізінде НОРМА тіліндегі жазба, берілген нақты есепті шешудің сандық әдісінің жазбасы болып табылады.

НОРМА тіліндегі жазбаларда артық ақпараттық байланыстар болмайтындығы да маңызды. Мұндай байланыстар әдетте бағдарламалау процесі барысында пайда болады, және олар алгоритмдер мен бағдарламаны ықшамдау кезінде анық көрінеді. Бағдарламалардың дәл ақпараттық құрылымын анықтау күрделі мәселе болып табылатыны белгілі. НОРМА тілі бізге бағдарламаның тізбекті этапын өткізуге мүмкіндік береді, ал параллель бағдарламаны генерациялау үшін бірден математикалық формулалар терминіндегі жазбасынан бастауды ұсынады. Бұл пайымдау бойынша, dataflow-компьютерлерін бағдарламалау үшін НОРМА тілінің потенциалын зерттеу өте қызықты болары анық.

Алынған нәтижелер авторлармен шынайы транслятор-синтезатор құру барысында пайдаланылды. НОРМА тілінің сипаттауы бойынша, ол тізбекті компьютерлер үшін де, таратылған жадылы және ортақ жадылы параллель есептеу жүйелері үшін де шығыс бағдарламаларын алуға мүмкіндік береді. Бұл бағдарламалар Fortran MPI, Fortran PVM, Fortran 77 және Fortran тілінің басқа да диалектілерінде жазылуы мүмкін.

Төменде НОРМА тілінің қысқаша сипаттамасы жұмыс стандарты [1] және http:// www.keldysh.ru/norma сайтының деректері бойынша беріледі.

НОРМА тіліндегі бағдарлама бір немесе бірнеше бөлімдерден тұрады. Бөлімдер үш түрлі болуы мүмкін – негізгі (басты) бөлім, қарапайым бөлім және функция-бөлім. Бөлімнің түрі сәйкесінше MAIN PART, PART және FUNCTION кілттік сөздерімен анықталады. Бөлімдер бір-бірін өз атауларымен шақырулары және деректерді формальды және фактілік параметрлер механизмі, болмаса сыртқа файлдар арқылы INPUT және OUTPUT сипаттамалары көмегімен жіберуі мүмкін. Бөлімдерді рекурсивті шақыруларға тыйым салынған.

НОРМА тілінде ауқымды айнымалылар түсінігі жоқ.

Бағдарламада, RESULT кілттік сөзіне дейінгі формальды параметрлер тізімінде көрсетілген барлық параметрлер бастапқы деректер, ал ол кілттік сөзден кейінгі келтірілген параметрлер есептеу нәтижелері болып есептеледі. Бір параметр бір мезгілде бастапқы және нәтиже бола алмайды, себебі бұл айнымалылардың мәндерді қайта меншіктеуіне алып келеді, ал НОРМА тілінде қайта меншіктеуге рұқсат етілмейді. Функция-бөлімінде RESULT кілттік сөзі қолданылмайды, себебі функцияны есептеу нәтижесі функцияның атауымен және типімен байланыстырылады.

Бөлім денесінде сипаттаулар, операторлар және итерациялар берілулері мүмкін. Олардың орналасу тәртібі, жалпы айтқанда еркін – мүмкін болатын шектеулер транслятордың кіріс тілін сипаттау кезінде анықталады.

НОРМА тілінің базалық ұғымы облыс болып табылады. Облыс - бұл n-өлшемді индексті кеңістікте нүктелер координатасын беретін

{i₁, …, i_n}, n > 0, i_j > 0, j=1…n,

түріндегі бүтінсанды жиынтықтар бірігуі. Есептің n-өлшемді кеңістігінің әрбір координат өсімен индекс аты байланыстырылады.

Бірөлшемді облыс үғымы, облыстарды сипаттау кезіндегі басты маңызды ұғым болып табылады. Бірөлшемді облыс, индекстік кеңістіктегі қандай да бір координат өсінде нүктелер диапазонын беру үшін қызмет етеді. Дербес қарапайым жағдайда бірөлшемді облысты сипаттау кезінде, бірөлшемді облыстың аты, индекс аты және индекс мәндерінің өзгеру шекаралары көрсетіледі. Мысалы, НОРМА тілінің келесі екі сипаттаулары:

ks : (k = 1..n).

js : (j = 1..10).

бірөлшемді екі облысты енгізеді. Бірінші жағдайда, үстінгі шекара n параметрінің көмегімен берілген (барлық параметрлердің мәндері параметрлерді сипаттау бөлімінде сипатталуы керек). Екінші жағдайда өлшем айқын көрсетілген. Диапазон шекаралары болып, бүтін тұрақтылардан, облыс параметрлерінен және арифметикалық операциялардан тұрғызылған бүтін оң тұрақты өрнектер алынады.

Көпөлшемді облыс «;» таңбасымен белгіленетін облыстарды көбейту операциялары көмегімен тұрғызылады. Төменде бірөлшемді облыстарды Dirk және Dirl көбейту операциясы көмегімен алынған екіөлшемді облысты сипаттау мысалы көрсетілген:

Square: ( DirK: (k=1..15); DirL: (l=1..5))

Енгізілген тікбұрышты square облыс екіөлшемді индексті кеңістіктің ішкі жиыны болып табылады. Оған бірінші координатасы 1 ден 15-ке дейін, ал екіншісі 1 ден 5-ке дейінгі мәндер болатын нүктелер кіреді.

Тікбұрышты А және В облыстарын көбейту «;» операциясы коммутативті қасиетке ие, яғни А;В=В;А. Бұл, дербес жағдайда, облысты сипаттау кезінде, индексті кеңістік бағыттарының реті бекітілмейтінін білдіреді. Егер индексті кеңістік бағыттарын бекіту қажет болса, онда INDEX кілттік сөзі көмегімен облыс индекстерінің сипаттауы беріледі.

Барлық облыстарды айқын түрде сипаттау міндетті емес, мұнда енгізіліп қойылған атауларды да пайдалануға болады. Мысалы,

NewGrid: (ks;js).

жоғарыда анықталған ks және js бірөлшемді облыстары арқылы облысты анықтайды. Енгізілген облыстарды өзгертуге болады. Облыстарды модификациялау (өзгерту) бірнеше нүктелер санын қосу, нүктелерді жою немесе диапазонын өзгерту арқылы орындалуы мүмкін. Екі алғашқы типтерді модификациялау LEFT(n) және RIGHT(n) шекара функциялары көмегімен сипатталады. LEFT(n) функциясы диапазонның сол жақ шекарасына, ал RIGHT(n) функциясы – диапазонның оң жақ шекарасына қолданылады. Функция алдына қойылған «+» таңбасы бірөлшемді облысқа нүктелер қосылатынын, ал «-» таңбасы бірөлшемді облыстан нүктелер жойылатынын білдіреді. Бұл екі функцияда, облыстан жоюға немесе облысқа қосуға қажетті нүктелер санын анықтайтын бір ғана параметр n болады. LEFT және RIGHT функцияларының нақты параметрлері ретінде тек бүтін оң тұрақты берілуі мүмкін. Функцияларға қатынас, модификация жасалатын диапазонды беретін бір өлшемді облыс атымен тек контексте ғана мүмкін болады. Бағдарламада келесі сипаттау бар делік:

DirK:(k=1..15)

Онда k=3..18 нүктелерінен тұратын DirKm облысын келесі түрде беруге болады:

DirKm: DirK-LEFT(2)+RIGHT(3)

Диапазонды айқын түрде қайта анықтай отырып, құрамдас бірөлшемді облысты өзгертуге болады. Ол үшін модификацияда индекс аты мен оның жаңа мәнін көрсету керек. Бағдарламада келесі сипаттау бар делік:

Square: (DirK:(k=1..15); Dirl: (l=1..9))

Жасалған сипаттауды модификациялау үшін және бір индекс бұрынғыша 1-ден 15-ке дейін өзгеретін, ал басқасы 10-нан 22-ге дейін өзгеретін облысты анықтау үшін, келесі конструкцияны пайдалануға болады:

SquareNew: Square/l=10..22

Облыс индекстерін байланыстыратын қарапайым қатынастар көмегімен облысты модификациялау мүмкіндігі бар. Мысалы,

KL: ((k=1..10);(l=1..10)). Diagonal: KL/k=1

сипаттауы (k=1,l=1), (k=2,l=2), … ,(k=10,l=10) нүктелерінен тұратын Diagonal облысын береді.

Айта кету керек, облыс тек қана индексті кеңістік нүктелері координаттарының мәндерін ғана анықтайды (осы нүктелердегі есептеу шамаларының мәндері емес). Егер Y_ij, i, j=1…n шамасының мәндерін, есепті шешу барысында X_ij=F(i, j) формуласымен енгізілген X_ij, i, j=1…n торында есептеу талап етілсе, онда келесі қадамдар тізбегін орындау керек:

1. i, j=1…n нүктелерінен тұратын облысты сипаттау.

2. Осы облыста Х және У шамаларын сипаттау.

3. Осы облыста X_ij=F(i, j) торының және Y_ij=G(X_ij) мәндерін есептеу ережесін беру.

НОРМА тілінде облыстарды айқын сипаттаумен қатар, шартты облыстарды беру мүмкіндігі де қарастырылған. Индекстік кеңістік нүктелерінің шартты облысқа кіруі немесе кірмеуі, қандай да бір шарттың орындалуы немесе орындалмауына байланысты анықталады. Шартты облысты беру идеясы қарапайым. Ертерек анықталған D облысы екі қиылыспайтын D₁ және D₂ ішкі облыстарға бөлінеді. Бірінші ішкі облыс берілген шарт ИСТИНА мәнін қабылдайтын D облысының нүктелерінен, ал екінші ішкі облыс берілген шарт ЛОЖЬ мәнін қабылдайтын нүктелерден тұрады. Square облысының алдыңғы сипаттамасын алып, соның негізінде шартты облыстарды берейік:

Square1, Square2: Square/x[k,1]-y[k,1]<eps

Берілген сипаттама бастапқы облысты Square екі қиылыспайтын Square1 және Square2 ішкі облыстарға бөлуді береді, және Square1∩Square2=Ø, ал Square1USquare2=Square. Бірінші Square1 ішкі облысы, x[k,1]-y[k,1]<eps шарты ИСТИНА мәнін қабылдайтын Square облысының нүктелерінен тұрады, ал Square2 ішкі облысы, ЛОЖЬ мәнін қабылдайтын нүктелерден тұрады.

НОРМА тілінде шамалардың екі класы анықталған: скаляр шамалар және облыстағы шамалар. Сипаттама ағымды бөлімде әрбір шамаға сәйкес бірегей ат қояды, сонымен қатар шаманың типін береді: REAL, INTEGER немесе DOUBLE. Скаляр шаманы сипаттау, мысалы, келесі түрде болуы мүмкін:

VARIABLE k1,k2 INTEGER

VARIABLE pi DOUBLE

Әрбір облыстағы шамалар сипаттамада көрсетілген облыспен байланыстырылады. Бұл облыс, берілген шамаға қатынас кезінде индексті өрнектерде пайдаланылуы мүмкін индекс аттарын анықтайды. Индексті өрнектерді көрсету реті маңызды емес. Облысты сипаттау кезінде енгізілетіндіктен, индекстер үшін арнайы сипаттау талап етілмейді.

Тағы да Square облысының алдыңғы берілген сипаттамасын пайдаланайық және соның негізінде облыстағы шамаларды енгізейік:

Square: (DirK:(k=1..15); Dirl: (l=1..9))

VARIABLE Xsum, Y DEFINED ON Square

OneDimK DEFINED ON DirK, OneDimL DEFINED ON DirL

Келтірілген сипаттаулар Square облысында Xsum және Y шамаларын анықтайды. Индексті өрнектерде бұл екі шама да k және l индекстеріне ие болуы мүмкін. OneDimK және OneDimL шамалары DirK және DirL облыстарында анықталған, сондықтан олар индексті өрнектерде сәйкесінше k және l индекстеріне ие болулары мүмкін.

Облысты сипаттау кезінде индексті кеңістік бағыттарының реті бекітілмегендіктен, Y[k-1,l+1] және Y[l+1,k-1] қатынастары эквивалентті. Егер бір индексті бағытты басқасымен байданыстыру қажет болса, онда оны айқын түрде көрсету керек. Мысалы, Y матрицасының диагоналдық элементтерін Y[k,l=k] немес жай Y[l=k] деп анықтауға болады.

НОРМА тілінде операторлардың үш түрі ғана анықталған: скалярлық оператор, ASSUME операторы және бөлімді шақыру.

Скалярлық оператор скалярлардың арифметикалық мәндерін есептеуге арналған. Жалпы алғанда бұл оператор дәстүрлі бағдарламалау тілдеріндегі қабылдау операторының аналогы десе болады, сол жағында скаляр аты көрсетіледі, ал оң жағында – скалярлық арифметикалық өрнек. Мысалы:

d = 1997

c = b+e+SQRT(d+4)

Скалярлық операторда қайта меншіктеу рұқсат етілмейді, сондықтан k=k-1 түріндегі оператор анықтама бойынша дұрыс емес дептесептеледі.

ASSUME операторы облыста анықталған шамалардың арифметикалық мәндерін есептеу үшін пайдаланылады. Бұл оператордың семантикасы келесі түрде анықталады. Шартты түрде жазылған қатынасты қарастырайық:

FOR D(i₁,…,i_n) ASSUME

мұндағы:

• D(i₁,…,i_n) – ASSUME операторының облысы;

• (i₁,…,i_n) – D облысының индекстері;

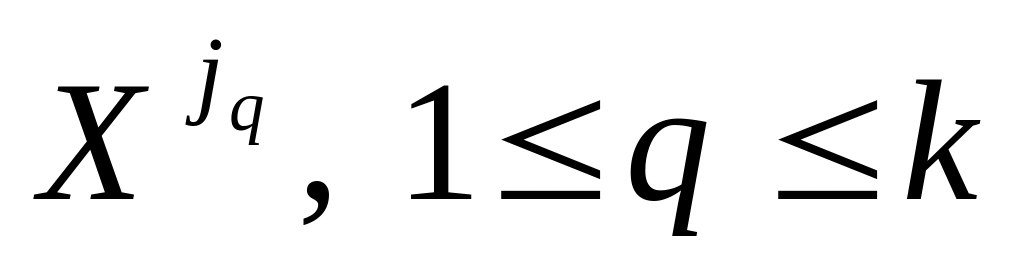• - облыста анықталған шамалардың аттары;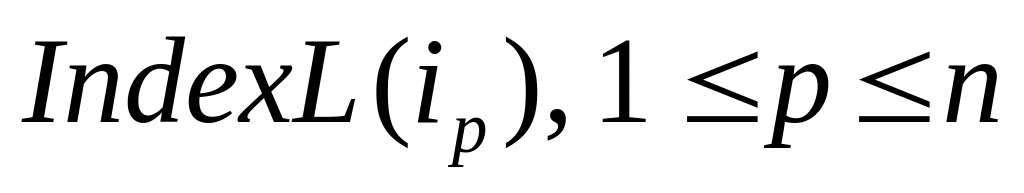

• - сол жақтағы индекстік өрнектер;

• - оң жақтағы индекстік өрнектер;

• F – оң жақтағы есептелетін функция;

• Other – оң жақтың басқа термалары.

Әрбір осындай қатынас, оң жақтағы шамаларының мәндері және Other термалары бойынша, сол жақтағы X^l шамасының мәнін есептеу F ережесін береді. Ол келесі түрде жүргізіледі:

• Барлық 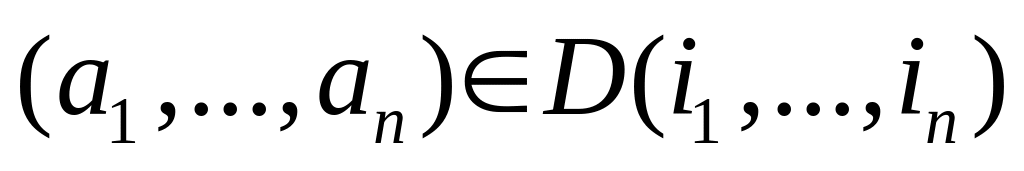нүктелері анықталады;

• Әрбір 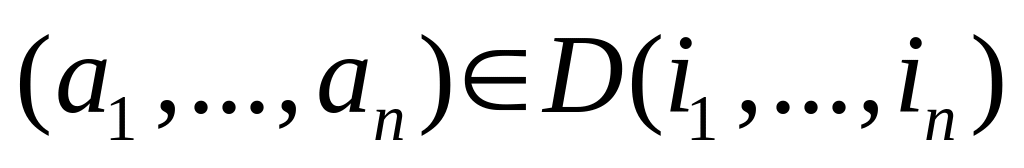нүктесі үшін 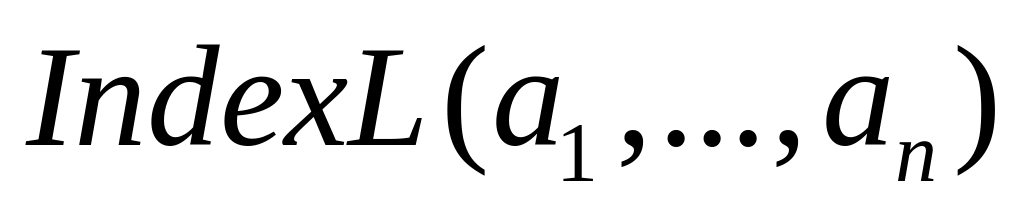нүктесінде сол жақтағы X^l шамасының мәнін есептеу талап етіледі;

• Әрбір нүктесі үшін барлық шамаларының индекстің өрнектерінің 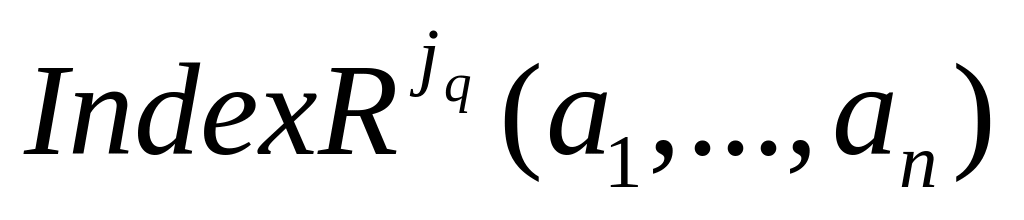мәндері есептеледі:

• Егер қандай да бір уақыт мезетінде нүктесі үшін Х барлық аргументтері есептеліп қойылса, онда сол жақтағы шамасының мәндерін есептеу мүмкін болады; ал егер аргументтер толық анықталмаса, онда дәл осы мезетте берілген нүктені есептеу мүмкін емес (бірақ ол тіпті мүмкін емес дегенді білдірмейді).

Берілген оператор шаманың мәндерін есептеу ережесін анықтайды. Сонымен қатар ол бағдарламаның берілген орнында есептеудің тез арада орындалуын талап етпейді және есептеу тәсілін немесе ретін белгілемейді. Оператор тізбекті болмаса параллель орындалу жайында ешқандай ақпаратты қамтымайды. Өзімізге таныс сипаттауларды қарастырайық:

Square: ( DirK: (k=1..15); DirL: (l=1..9))

VARIABLE Xsum, Y DEFINED ON Square,

Төменде келтірілген оператор

FOR Square ASSUME Xsum = 0

Xsum шамасының 135 элементін нөлдік етуді береді. НОРМА тілінде бұл сұраныстың іске асырылуы бекітілмейді.

Жалпы алғанда бұл параграфта НОРМА тілінің негізгі идеясын сипаттап өттік десек болады. Есептеу барысында қажет етілетін басқа да сұрақтар туралы толық мағлұматты [1] әдебиеттен табуға болады.

Параграфтың соңында НОРМА тілінде жазылған сызықты теңдеулер жүйесін Гаусс-Жордан әдісімен шешудің бағдарламасын қарастырайық. Аталған әдістің есептеу формулаларын келесі түрде жазуға болады:

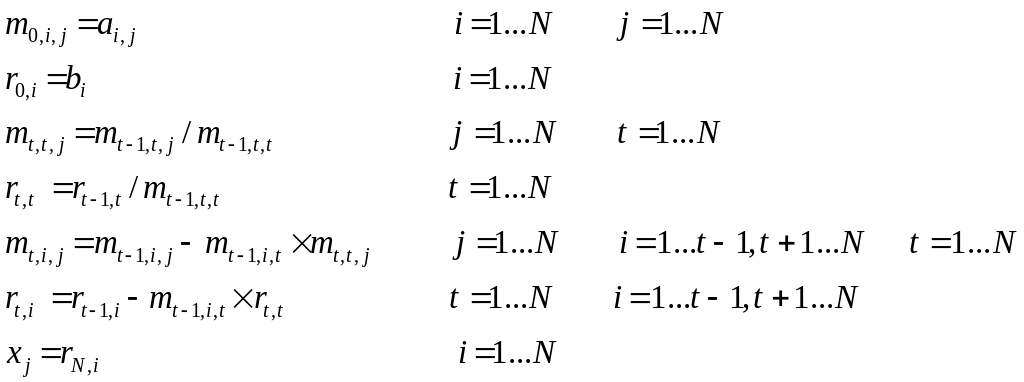
Бағдарлама тексті төменде келтірілген. Ондағы жолдардың нөмірленуі тілдің міндетті элементі болып табылмайды, ол тек операторлардың мағынасын кезекті түсіндіру үшін ғана пайдаланылған.

1 MAIN PART Gauss.

2 BEGIN

3 INDEX k,l.

4 ks : (k=1..n).

5 ls : (l=1..n).

6 kls : (ks; ls).

7 VARIABLE a DEFINED ON kls.

8 VARIABLE b, x DEFINED ON ks.

9 INPUT a (FILE=’gauss’) ON kls,

10 b(FILE=’gauss’) ON ks.

11 DOMAIN PARAMETERS n=4.

12 COMPUTE Calculate(a ON kls, b ON ks RESULT x ON ks).

13 OUTPUT x(FILE=’gauss.out’,TAB(10),’Решение:’,STR(1)) ON ks.

14 END PART.

15 PART Calculate.

16 a,b RESULT x

! Раздел вычислений

17 BEGIN

18 INDEX I,j

19 so:(ijs: is: (i=1..n); js: (j=1..n));ts: (t=0..n)).

20 slo: ts;is). s:so/ts-LEFT(1). Sl:slo/t=1..n.

21 VARIABLE a DEFINED ON ijs.

22 VARIABLE b, x DEFINED ON is.

23 VARIABLE m DEFINED ON so.

24 VARIABLE r DEFINED ON slo.

25 DOMAIN PARAMETERS n=4.

26 DISTRIBUTION INDEX i=2..8, j=1.

27 FOR so/t=0 ASSUME m=a.

28 FOR slo/t=0 ASSUME r=b.

29 sa,sb:s/i=t. sal,sbl:sl/i=t.

30 MACRO INDEX ti [t-1,i=t].

31 MACRO INDEX tij [ti,j=t].

32 FOR sa ASSUME m=m[ti]/m[tij].

33 FOR sal ASSUME r=r[ti]/m[tij].

34 FOR sb ASSUME m=m[t-1]-m[t-1,j=t] * m[i=t].

35 FOR sbl ASSUME r=r[t-1]-m[t-1,j=t] * r[i=t].

36 FOR is ASSUME x = r[t=n].

37 END PART

Бағдарлама операторларына түсініктеме берейік. Төменде пайдаланылған нөмірлер бағдарлама жолдарының нөмірлеріне сәйкес келеді.

(1) Gauss бағдарламасының басты бөлімінің тақырыбы.

(2) Басты бөлімнің басталуы.

(3) Облыстардың индекстерін сипаттау.

(4-6) Есептің бастапқы деректері анықталған is, js бірөлшемді облыстары және ijs көпөлшемді облысын анықтау.

(7-8) a, b, және x айнымалыларын сипаттау, мұндағы a – жүйе коэффициенттерінің матрицасы, b – бос мүшелер бағаны, x - жүйені шешу нәтижесі.

(9-10) gauss.dat файлынан бастапқы деректерді енгізу.

(11) Облыстар параметрін беру.

(12) Есептеу жүргізетін Calculate бөлімін шақыру.

(13) gauss.out файлына нәтижені шығару.

(14) Басты бөлімнің соңы.

(15) Calculate бөлімінің тақырыбы.

(16) Бөлімнің (a, b) кіріс және (х) шығыс параметрлерін белгілеу.

(17) Жәй бөлімнің басталуы.

(18) Облыстардың индекстерін сипаттау.

(19) ts және ijs облыстарынан тұратын көпөлшемді so облысын анықтау. Өз кезегінде ijs облысы is және js облыстарынан тұрады.

(20) Облысты модификациялау операциялары көмегімен s, s1 облыстары және slo шартсыз облысы анықталады.

(21-22) Бөлім параметрлері болып табылатын айнымалыларды сипаттау.

(23-24) m және r айнымалыларын сипаттау.

(25) Облыстар өлшемдерін беру.

(26) Таратылу индекстерін сипаттау.

(27-28) m және r айнымалыларының бастапқы мәндерін беру.

(29) Қосымша шартты sa,sb,sal,sbl облыстарын сипаттау.

(30-31) Индекстік конструкцияларды сипаттау. Индекстік конструкциялар күрделі индекстік өрнектердің жазылуын қысқарту үшін қолданылады.

(32-36) Сәйкес есептеу формулалары үшін есептеулер.

(37) Бөлімнің соңы.

Сұрақтар мен тапсырмалар

1. Т-жүйесінің артықшылықтар мен кемшіліктері.

2. Т-жүйесіне сәйкес келетін алгоритмдерге мысал келтіріңіз.

3. Т-жүйесінде дайын емес айнымалылармен қандай операциялар рұқсат етілген?

4. НОРМА тілі қандай есептерді шешуге арналған?

5. НОРМА тілін пайдалана отырып екі матрицаны көбейту бағдарламасын жазыңыз.

6. Алгоритмді математикалық формулалар көмегімен жазудың қандай артықшылықтары бар?

7. Скаляр шамалар және облыстағы шамалар дегеніміз не?

8. Шартты облыстар қалай беріледі?

9. Көпөлшемді облыстар қалай тұрғызылады?

10. RESULT кілттік сөзінің қызметі.

11. НОРМА бағдарламалау жүйесі туралы не айтасыз?