39 Сурет. Блокты-екідиагоналды жүйеге арналған Макрограф

Граф құрылымынан көрініп тұрғандай, егер (2.10) алгоритмін векторлы-матрицалық операциялар тізбегі ретінде қарастыратын болсақ, онда ол тізбекті болады және ол параллельденбейді. Іс жүзінде жеке алғанда әрбір макрооперация параллельденбейді. Сонымен бірге ол екідиагоналды жүйенің шешімін береді. Сондықтан, жүйенің оң жақ бөлігін есептеу процесі ғана параллельденуі мүмкін, егер де әрине жүйені (2.10) сияқты қайта шешетін болса.

Бұл фактілерден, қарастырылып отырған (2.9) жүйені шешу алгоритмін жақсы параллельдеу мүмкін емес деп қорытынды жасауға болар еді. Алайда бұндай қорытынды жасау асығыстық болады.

Блокты-екідиагоналды жүйені шешу алгоритмін зерттеп көрелік Алгоритмнің полиэлементті. Берілген матрица элементтері мен векторлардың жоғарыдағы жасалған белгілеулерін ескере отырып алатынымыз:

(2.11)

Бұл жағдайда барлық i, k үшін деп алынады. (2.11) формуласында b,f, e, x, d, y шамалары бойынша u шамасын есептейтін ең басты және жалғыз скалярлы операция

и=b^-1(f - ex - dy), (2.12)

Тағы да операцияны тиімсіз қарапайым қайта нөмірлеу. Алгоритм графын тұрғызу үшін тік бұрышты тор қарастырамыз және оның түйіндерінің (тораптары) координаталары i, к бүтінсанды деп алайық. Тордың барлық түйіндеріне 1 ≤ i ≤ n, 1 ≤ к ≤ m үшін граф төбелерін орналастырамыз және оларды (2.12) операцияларына сәйкес келеді деп санаймыз. Кіріс деректерімен және кейбір аргументтердің нөлдік мәндерімен жабдықтайтын төбелерді көрсетпейміз.

(2.11) өрнегін талдай келе, координатасы i, k болатын төбеге координаталары i - 1, k және i, k - 1 болатын төбелер сәйкес келетін операциялардың орындалу нәтижелері берілетініне көз жеткізу қиын емес. Координаталары i, k болатын операцияны іске асыруға қажетті қалған барлық деректер кіріс деректері болады және тек осы операцияны жүргізу үшін ғана керек. Бұл алгоритм графында (2.5) алгоритміндегі сияқты кіріс деректерін көптеп жіберу жоқ. n = 5, m = 9 болған жағдайдағы алгоритм графы 40-шы суретте көрсетілген. Одан алгоритм графы өте жақсы параллельденетінін көреміз. Максималды параллель форманың ярустары пунктирлі сызықтармен белгіленген. Кіріс деректерінің енгізілуін ескермеген кездегі алгоритмнің биіктігі m+n+1, алгоритмнің ені min(m, n). 41-суретте осы графтың төбелері пунктирлі сызықтармен біріктірілген. Осындай әрбір топ (бөлік) 39-шы суретте келтірілген графтың бір төбесіне сәйкес. Олар жалпыланған паралллель форманың ярустары болып табылады. Осы суреттерден жақсы параллельденетін алгоритмнің өзі операцияларды сәтсіз үлкейткенде қалай параллельденбеуі мүмкін екені көрініп тұр.

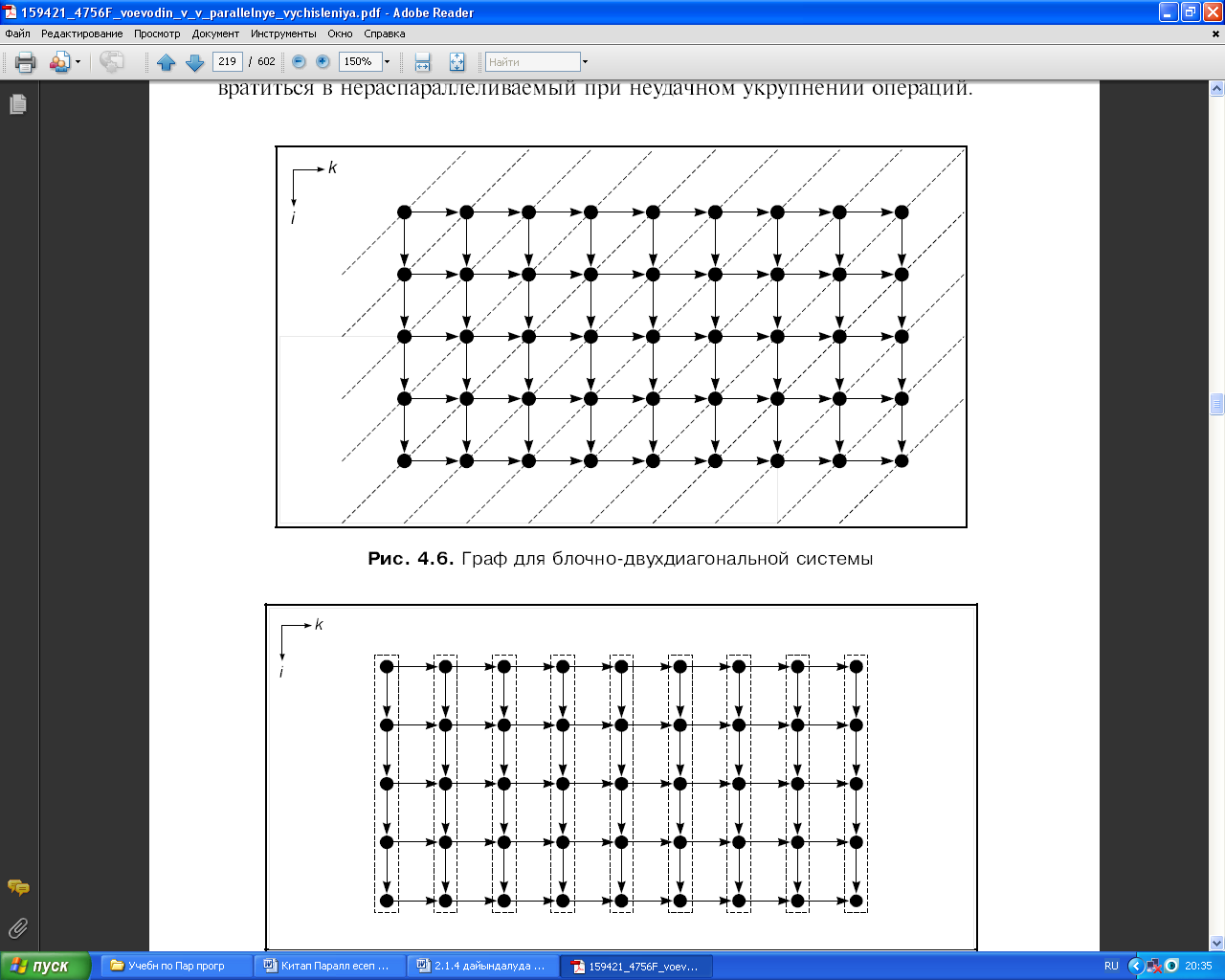
40 Сурет. Блокты-екідиагоналды жүйеге арналған граф

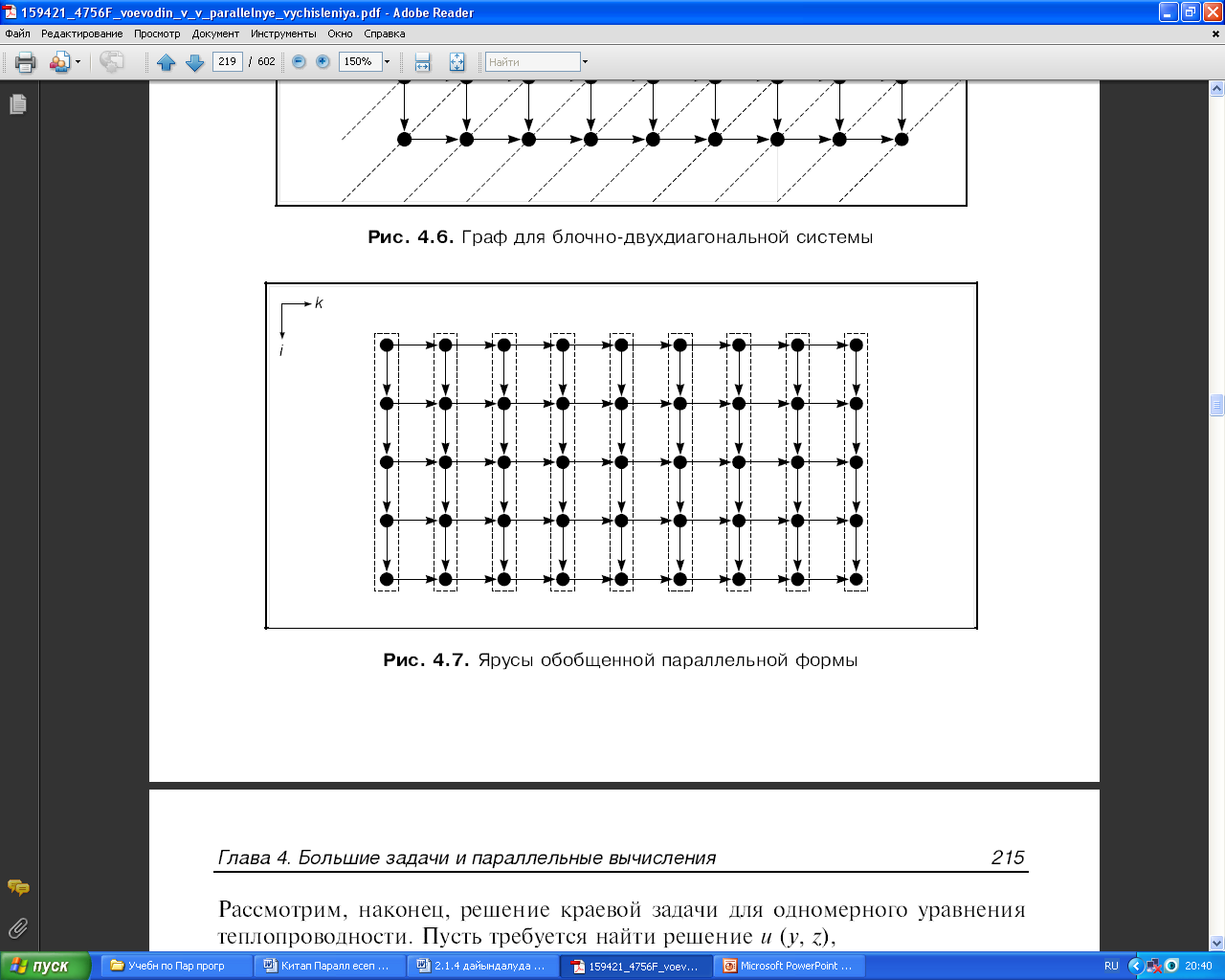
41 Сурет. Жалпыланған пралллель форманың ярустары

Мысал 3. Бірөлшемді жылу өткізгіштік теңдеуі үшін шектік есебін шешу жолын қарастырайық. Бізден u (у, z) шешімін табу талап етілсін,

мұндағы

h қадамымен z және τ қадамымен у бойында бірқалыпты тор тұрғызайық. Қандай да бір себептерге байланысты айқын схема таңдап алынды делік.

Алгоритм келесі формулаға сәйкес іске асырылатын болсын.

(2.13)

Алгоритм графын тұрғызу үшін i, j остерімен тік бұрышты координат жүйесін енгізейік. Берілген айнымалылар z, у және i, j арасындағы байланыс

қатынасымен беріледі.

Бүтінсанды тордың әрбір торабына граф төбесін орналастырамыз және оны a, b, c аргументтерінің әртүрлі мәндері үшін орындалатын келесі скаляр операцияға сәйкес келеді деп есептейміз.

(2.14)

Алгоритм графы h = 1/8, τ = Т/6 жағдайы үшін 42 а, б - суретінде көрсетілген. Облыс шекарасында төбелер орналасқан, олар бастапқы деректердің және шектік мәндердің енгізілуін білдіреді.

Бұл мысалда алгоритмдердің кезкелген компьютерде іске асырылуына қатысты өте маңызды сұрақ та қарастырылады. Бұған дейін біз оны операциялардың параллельді форманың қабаттары бойынша орындалуымен байланыстырған болатынбыз. Әрине, бір қабаттың операциялары бір-біріне тәуелді емес және оларды әр түрлі құрылғыларда бір мезгілде орындауға болады. Бірақ, параллель есептеуді осылай ұйымдастырудың тиімділігі өте төмен болуы мүмкін. 42, а – суретте, (2.13) алгоритмінің максималды параллель формасының барлық ярустары пунктирлі сызықтармен көрсетілген. Операциялар осы ярустар бойынша орындалады делік.

Бір ярустың (2.14) түріндегі әрбір операциясы үш аргументті талап етеді. Олар алдыңғы яруста орындалған операциялардың нәтижелері болып табылады. Егер, бір яруста алынған деректердің жадыдан тез алынуы мүмкін болса, онда алгоритмді параллель форманың ярустары бойынша іске асыруда ешқандай маңызды қиыншылықтар туындамайды. Дегенмен, үлкен көпөлшемді есептер үшін ярустар үлкен масштабты болып, олар туралы ақпарат жылдам жадқа сыймай қалуы мүмкін. Онда оларды орналастыру үшін баяу жадты пайдалануға тура келеді. Бұл жады үшін бір санның таңдалу уақыты (2.14) базалық операциясының орындалу уақытынан әлдеқайда асып түседі. Ол дегеніміз кезекті ярусқа өту кезінде операцияны орындауға жұмсалған уақыт жадымен өзара қатынас уақытынан біршама аз уақытты алуы мүмкін дегенді білдіреді. Операцияның орындалу уақытының жадыға қатынау уақытына қатынасы неғұрлым аз болса, параллель форманың ярустары бойынша (2.13) алгоритмін іске асырудың тиімділігі соғұрлым төмен болады. Бұл жағдайда, параллель компьютердің жұмыс уақытының басым бөлігі есептеуге емес, баяу жадпен деректер алмасуға жіберіледі.