38 Сурет. Үшбұрышты жүйелерге арналған графтар

Бұл суретте параллельді форманың ең максималды түрінің бірі көрсетілген. Оның ярустары пунктирлі сызықтармен белгіленген. Егер a_ij элементтерінің енгізілуіне сәйкес келетін төбелерді бірінші яруске орналастырса, онда параллельді форма канондық болады. а — bс түріндегі операциялар енетін ярустардың жалпы саны n - 1 тең. Бірінші яруста b векторының элементтерін енгізу операциялары орналасқан.

Егер (2.6) өрнегіндегі қосындыны есептеуде біз қандай да бір оймен қосудың тізбекті әдісіне тоқтаған болсақ, онда j индексінің өсуі бойынша қосуды таңдау жалпы кездейсоқ жасалған болатын. Бұл таңдаудың қандай да бір артықшылықтары көрініп тұрмағандықтан кері қоюдың алгоритмін j индексінің кемуі бойынша қосу арқылы тұрғызуға болады. Онда оған сәйкес алгоритм келесі түрде болады:

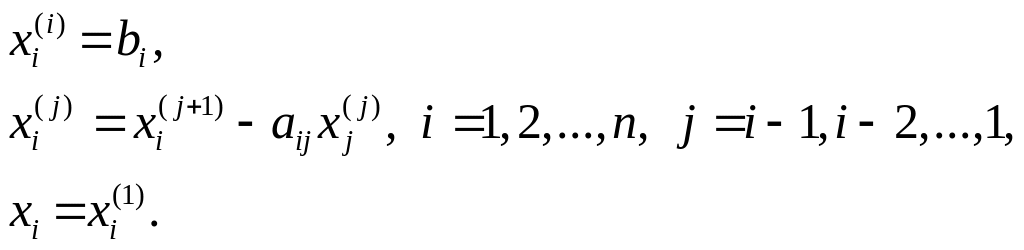(2.8)

Оның графы n = 5 жағдайы үшін 40, б-суретте көрсетілген. Енді жоғарғы бұрыштағы төбе координатасы i = 1, j = 1 болатын нүктеде орналасады. Қандай да бір параллель форманың ярустарына a - bс түріндегі операцияларға сәйкес келетін төбелерді орналастыра отырып, ондағы әрбір яруста әрқашанда тек бір төбе ғана бола алатынын байқаймыз. Бұл 40-шы суретте графтың барлық төбелері бір жолда жатуымен түсіндіріледі. Бұл жол пунктирлі бағыттармен көрсетілген. Сондықтан (2.8) алгоритмі графындағы a – bc түріндегі операцияларды қамтитын ярустардың жалпы саны әрқашан (n² – n + 2)/2 тең болады, бұл (2.7) алгоритмі графындағы n-1 ярустар санына қарағанда әлдеқайда көп.

Күтпеген нәтиже алынды десе болады. Шынында, екі алгоритм де (2.7) және (2.8) бір ғана есепті шешуге арналған, олар (2.6) бірдей формулалары негізінде құрылған және дәл есептеулерге қатысты алсақ эквивалентті. Екі алгоритм де бірдей жады көлемін және азайту, көбейту операцияларының бірдей санын талап ететіндіктен, бірпроцессорлы компьютерлерде іске асырылу жағынын алғанда олар бірдей.

Дегенмен, екі алгоритм графтарының бір-бірінен айтарлықтай айырмашылығы бар. Егер бұл алгоритмдерді n әмбебап процессордан тұратын параллель есептеу жүйесінде іске асырса, онда (2.7) алгоритмін n-ге пропорционал уақыт ішінде, (2.8) алгоритмін тек n²-қа пропорционал уақыт ішінде іска асыруға болады. Бірінші жағдайда процессорлардың орташа жүктелуі 0,5-ке, екінші жағдайда 0-ге жуық болады.

Сонымен, қарапайым компьютерлерде іске асырылуы жағынан қарағанда бірдей болатын алгоритмдер, параллель компьютерлерде іске асырылу кезінде мүлдем әртүрлі болулары мүмкін. Осы мысалды қолдана отырып айта кететін нәрсе, параллель компьютерлерді математикалық тұрғыдан игерудің басты қиындықтары да осы фактінің негізінде жатыр. Көптеген жылдар бойы «қарапайым» компьютерлерде жұмыс істейтін әртүрлі мамандық иелері, алгоритмдерді негізінен олардың 3 сипаттамасы бойынша бағалайды: операция саны, талап етілетін жадының көлемі және дәлдігі. Осы сипатттамалар негізінде барлығы дерлік тұрғызылды: есептеу техникасының негізгі параметрлері, есептеу ісіне үйрету процесі, есептеу әдістері және алгоритмдерін құрастыру, тиімділікті бағалау, тілдерді және трансляторларды құрастыру және көптеген т.б. Параллель есептеу жүйелерін құруда, алгоритмдерден, принципиалды түрде басқа қасиеттері мен сипаттамалары талап етілді, ал оларды білу тізбекті компьютерлер үшін қажеті де болмаған еді. Сонымен алгоритмдерді тереңірек зерттеу, олардың параллель қасиеттерін оқып үйрену, параллельділікті анықтау үшін конструктивті әдістемелігін құрастыру қажетті де маңызды іс-шаралардың қатарына жатады.

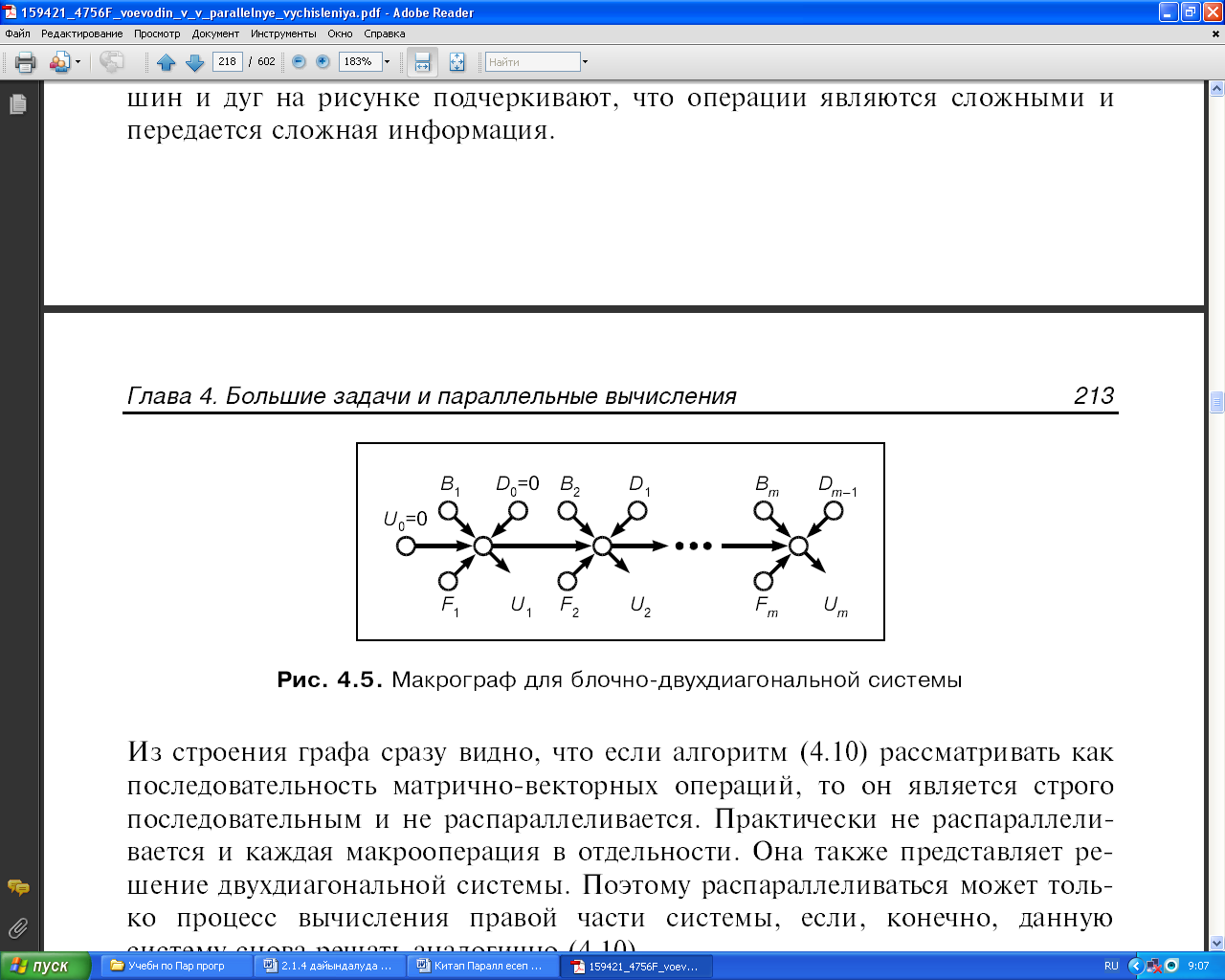
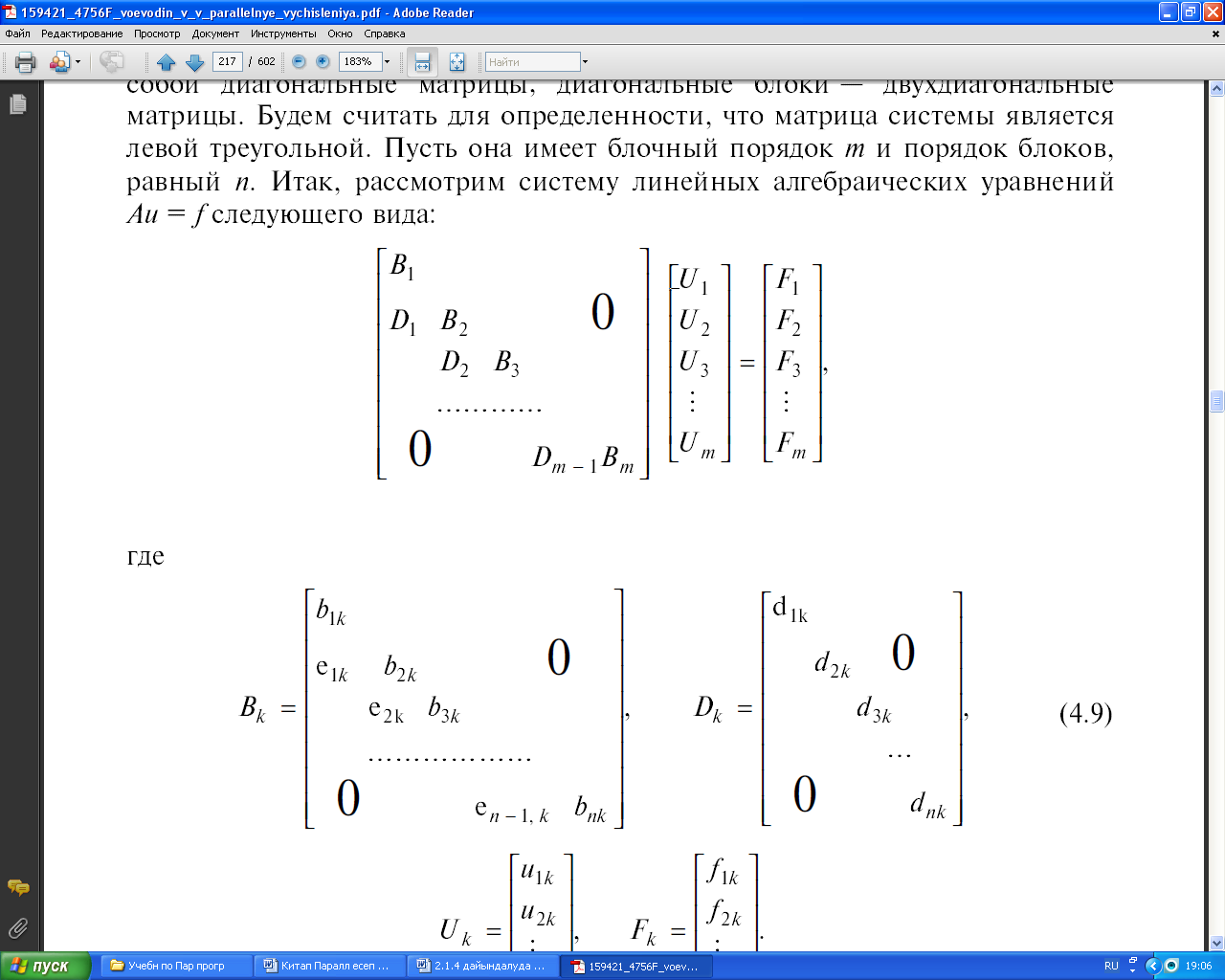
Математикалық физика теңдеулерін торлар әдістерімен шешу кезінде пайда болатын сызықты алгебраның көптеген есептерінің ішінде, блокты-екідиагоналды матрицалы сызықты алгебралық теңдеулер жүйесін шешу есебі жиі кездеседі. Мұндағы диагоналдық емес блоктар диагоналды матрицалардан тұрады, ал диагональ бойындағы блоктар – екідиагоналды матрицалар. Анығырақ болу үшін, жүйенің матрицасы сол жақты үшбұрышты болсын деп есептейік. Матрицаның блоктық реті m, ал блок реті n болсын. Сонымен, Au = f түріндегі сызықты алгебралық теңдеулер жүйесін қарастырайық [10].

мұндағы

(2.9)

Егер U₀ = 0, D₀ = 0 деп алатын болсақ, блокты – екідиагоналды жүйенің (2.9) шешімі рекуррентті анықталады:

U_k = B_k^-1(F_k – D_k-1U_k-1), 1 ≤ k ≤ m (2.10)

Х = В^-1(F — DY) макрооперациясы, F, Y векторлары және В, D матрицалары бойынша Х векторын есептейді. Әрбір төбесі осы макрооперацияға сәйкес келеді деп есептей отырып, (2.9) алгоритмінің графын тұрғызамыз. Ол 39-шы суретте көрсетілгендей болады. Төбелердің және доғалардың үлкен көлемі, бұл операциялардың күрделілігін және күрделі ақпарат берілетінін көрсетеді.