14 Сурет. Ортақ шиналы мультипроцессорлық жүйе.
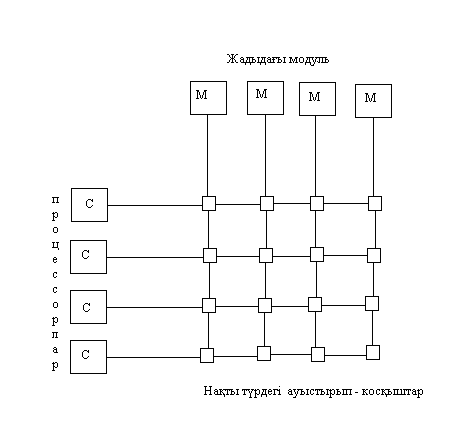
15 Сурет. Матрицалық коммутаторлардағы
мультипроцессорлық жүйе.
Каскадты айырып/қосқыштарды пайдалану – альтернативті әдіс болып есептеледі, мысалы, омега – желі жасалғандай. 16-суретте екі каскадта ұйымдасырылған, 4 коммутатордан 2*2 тұратын желі көрсетілген.
Әрбір пайдаланылған коммутатор өзінің кезкелген екі кірісін, өзінің кез–келген екі шығысымен байланыстыра алады. Бұл қасиет және пайдаланылған коммутация сызбасы осы суретте көрсетілген кезкелген есептеу жүйесінің процессорына жадының кезкелген модулімен қатынасуға мүмкіндік береді. Жалпы жағдайда n процессорды жадының n модулімен байланыстыру (жалғау) үшін, әрбірінде n/2 коммутатор болатын log2n каскад қажет етіледі, яғни жалпы алғанда барлығы (nlog2n)/2 коммутатор.
Үлкен n мәндері үшін бұл шама n2 қарағанда едәуір жақсы, бірақ басқа түрдегі қиындық туындайды – олар бөгелулер. Әрбір коммутатор лезде қосыла алмайды, себебі әрбір каскадта кіріс пен шығысты коммутациялауға біраз уақыт қажет етіледі. Тағы да айырып/қосылу уақыты үлкен емес қымбат қатынас жүйесі және үлкен бөгелістерге ие қымбат емес жүйелер арасындағы компромисс ізделінеді.
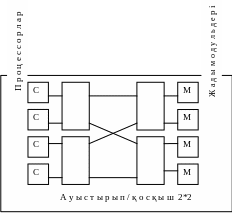
16 Сурет. Омега - желі мультипроцессорлық жүйесі.
Біз процессорлардың жады модульдерімен байланыс түрлерін толық қарастырған жоқпыз. Негізінде таратылған жадылы жүйелердегі нақты пайдаланылатын процессорлар коммутациясының сызбалары едәуір көп.
17, а-суретте, барлық есептеу тораптары бір сызық бойына біріктірілген қарапайым нұсқадағы байланыс топологиясы келтірілген. Жүйенің бірінші және соңғысынан басқа әрбір торабының оң және сол жақтарында көршілес тораптар орналасады. n тораптан тұратын жүйені тұрғызу үшін жүйеге n-1 байланыс қажет. Жүйенің екі торабының арасындағы жолдың орташа ұзындығы n/3–ке тең. Егер есептеу тораптарының сызықты түрін дөңгелек түрге өзгертсе, онда жолдың орташа ұзындығын азайтуға болады (17 б сурет). Сонымен, жүйедегі бірінші торапты соңғысымен қосымша байланыстыру арқылы, біз шын мәнінде жаңа топологияда қосымша пайдалы екі қасиет аламыз. Біріншіден, екі торап арасындағы жолдың орташа ұзындығы n/3-тен n/6-ға дейін қысқарады. Екіншіден, кез-келген тораптар арасындағы ақпарат алмасу екі тәуелсіз бағыт арқылы жүргізілуі есебінен, жүйенің жалпы істен шығуға тұрақтылығы артады. Әзірге барлық байланыс жұмысқа жарамды болып тұрғанда, ақпарат беру (алмасу) қысқа жолмен жүретін болады. Ал егер, қандай да бір байланыс бұзылатын болса, онда беру қарама-қарсы бағытта болуы мүмкін.
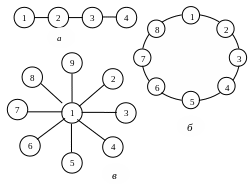
17 Сурет. Мультикомпьютерлерлік жүйелер байланыс топологияларымен: а – сызықша; б – дөңгелек; в – жұлдызша
Тікелей байланыстардың айқын шектелуіне қарамастан, тек көрші процестердің өзара байланысы қажет болатын ұқсас қарапайым «сызықты» топологиялар көптеген алгоритмдерге жақсы сәйкес келеді. Атап айтқанда, математикалық физиканың көптеген бірөлшемді есептері (және көпөлшемді есептер аймақты бірөлшемділерге бөлу арқылы) осындай ұқсас әдістермен жақсы шешіледі. Бұндай есептер үшін ешқандай басқа топологияларды ойлап табудың қажеті жоқ. Алайда, барлық есептер мұндай бола бермейді. Бұндай топологияларға қосарлану схемасын немесе сызықты алгебраның блоктық әдістерін тиімді іске асыру оңай емес, өйткені процестерді процесссорлар бойынша дұрыс орналастырмау уақыттың көп бөлігін қатынасқа (коммуникацияға) жоғалтуға әкеліп соғады. Идеалды жағдайда пайдаланушы бұл туралы ойламау керек, онда басқа да проблемалар жеткілікті болары анық, бірақ іс жүзінде ғажайыптар болмайды. Қазіргі таңда технологиялық себептерге байланысты, әрбір процессоры басқа барлық процессорлармен тікелей байланыста болатын үлкен мультикомпьютерлік жүйелерді жасауға болмайды. Олай болса, мұнда да, есептеу жүйелерін құрастырушыларға әмбебаптық пен мамандандырылғандықтың, күрделілік пен қолжетімділік арасындағы ымыраға келуді іздеуге тура келеді. Егер есептер класы алдын-ала анықталған болса, онда жағдай көп жеңілденеді де нәтиже жеңіл табылуы мүмкін.
Мысалы, параллель процестер арасында жұмысты бөлу сызбасын пайдалану, клиент-сервер сызбасындағы сияқты бір басты процесс бағыныңқы процестерге тапсырма тарататын (шебер/жұмысшылар схемасы немесе mаster/slaves), «жұлдыз» топологиясына (17, в сурет) жақсы сәйкес келеді. Жұлдыз сәулелерінде орналасқан есептеу тораптары өзара тікелей тәуелді байланыста болмайды. Бірақ бұл шебердің орталық торапта орналасу шартына байланысты процесс-шебердің бағыныңқы процестермен тиімді өзара байланысуына ешқандай да кедергі жасамайды.
Нақты есептеу жүйесінде процессорлар байланысы топологиясының қандай да бір түрлерін таңдап алу әртүрлі себептерге тәуелді болуы мүмкін. Бұл дегеніміз - технологиялық іске асыру, бағдарламалау мен жинау қарапайымдылығы, сенімділігі, тораптар арасындағы орташа жолдың минималды болуы, тораптар арасындағы максималды жолдың минималды болуы, бағасының қолжетімдігі т.б.
Кейбір нұсқалар 18-ші суретте көрсетілген. Екі өлшемді тордың топологиясы (18, а - сурет ) өткен ғасырдың 90-жылдарының басында i860 процессорлары негізінде Intel Paragon суперкомпьютерін құрастыруда пайдаланылған. Екі өлшемді тор топологиясына сәйкес (18, б – сурет), Dolphin Interconnect Solutuions компаниясы ұсынған SCI желісін пайдаланатын кластерлердің есептеу тораптары байланыстырылуы мүмкін. Осылайша, МГУ НИВЦ (Россия) кластерлерінің біреуі құрылған. Қазіргі таңда Dolphin компаниясы тораптарды үш өлшемді торға біріктіруге мүмкіндік беретін желілік кешенді ұсынуда. Тораптар арасындағы орташа ара-қашықтық неғұрлым аз болса, соғұрлым сенімділігі жоғары болады. Яғни, әрбір процессоры басқа барлығымен тікелей байланыс орната алатын топология ең жоғары нәтижелі деп саналады (18, в - сурет). Бірақ, қазіргі заманғы технология деңгейінің мұндай мүмкіндігі жоқ (армандауға да мүмкінік бермейді): жалпы байланыс саны n(n-1)/2 болғанда, әрбір тораптың байланысы n-1.
Кейде ерекше қызық нұсқалар табылады, соның бірі екілік гиперкуб топологиясы (18, г - сурет). n - өлшемді кеңістікте бірлік n - өлшемді кубтың тек төбелерін ғана қарастырамыз, яғни, хі координаталарының бәрі 0-ге немесе 1-ге тең (x1,x2,…,xn) нүктелері. Осы нүктелерге шартты түрде жүйе процессорларын орналастырамыз, әр процессорды жақын тұрған тікелей көршісімен әрбір n - өлшемді жағалай байланыстырамыз. Нәтижесінде N=2n процессордан тұратын жүйе үшін n - өлшемді куб аламыз. Екі өлшемді куб жай шаршыға, ал төртөлшемді нұсқасы шартты түрде 18, г-суретінде бейнеленген. Гиперкубта әрбір процессор тікелей log2N көршісімен байланысқан (толық байланыс жағдайында N көрші процессорлармен). Гиперкубтың пайдалы қасиеттері көп. Мысалы, әр процессор үшін олардың барлық көршілерін анықтау қиын емес: олар одан қандай да бір хі координатасының мәні бойынша ажыратылады. n-өлшемді гиперкубтың әрбір «қыры» n-1 өлшемді гиперкуб болып табылады. n-өлшемді гиперкуб төбелері арасындағы максимал арақашықтық n-ге тең. Гиперкуб өзінің тораптарына қатысты симметриялы: әр тораптан жүйе біркелкі болып көрінеді және арнайы өңдеуді қажет ететін тораптар болмайды. Көптеген алгоритмдер өз құрылымы бойынша процессорлар арасындағы осындай өзара байланысқа жақсы сәйкес келетінін айта кету керек.
Алгоритмнің әр қадамы жүргенде гиперкуб өлшемі бір бірлікке азаяды.
