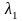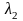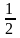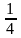3. Методы выпуклого программирования. Метод множителей Лагранжа

Методы выпуклого программирования, реализующие поиск минимума выпуклой функции или максимума вогнутой на выпуклом множестве планов.

Если множество планов - выпуклый многогранник, то эти методы допускают использование симплексного метода.

Наиболее эффективно эти и другие методы решения действуют для так называемых сепарабельных функций, т.е. функций, представимых в виде суммы функций одной переменной

F(X₁, X₂, .. ,X_n) = f₁(X₁) + f₂(X₂) + ... + f_n(X_n).

При решении многих задач нелинейного программирования определенный эффект дает метод множителей Лагранжа.

Пусть требуется найти экстремумы функции F(X) при условиях f_i(X)=0 (i = 1 .. m).

Функция   называется функцией Лагранжа и коэффициенты _i - множителями Лагранжа.

Можно доказать, что необходимым условием экстремума исходной задачи является обращение в нуль всех частных производных функции Лагранжа.

Например, при поиске максимума F(X₁, X₂) = X₁+X₂ при единственном условии X₁²+X₂²=1 строится функция Лагранжа

Строим систему уравнений

решение которой дает   и экстремальные значения целевой функции 

Для определения типа найденного экстремума можно построить матрицу вторых производных F(X), вычисленных в экстремальной точке, и определить знаки главных ее миноров. Если все они положительны, то найден минимум; если они чередуются, начиная с минуса, то найден максимум (правило Сильвестра).

Сам по себе метод множителей Лагранжа не дает существенного эффекта из-за необходимости решать, как правило, нелинейную систему уравнений; не гарантирует тип отыскиваемого экстремума, кроме глобальных дает и множество локальных экстремумов, но полезен при генерации идей и создании методов нелинейного программирования.

1. . Теорема Куна-Таккера

Пусть задача нелинейного программирования имеет вид

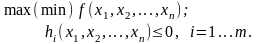
Для решения поставленной задачи используется центральная теорема математического программирования – теорема Куна-Таккера, выдвигающая необходимые условия существования решения задачи нелинейного программирования. Достаточные условия существования решения формулируются в теоремах Куна-Таккера второго, третьего и т.д. порядках и в данном курсе не рассматриваются.

Теорема (Куна-Таккера) Точка 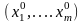может являться решением задачи нелинейного программирования только в том случае, если в ней выполнены следующие условия:

1) ;

2) ;

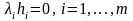3) , .

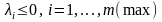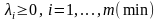Пример Найти наибольшее и наименьшее значения функции 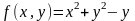при заданных ограничениях при ограничениях 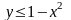и .

Решение. Запишем ограничения в стандартном виде

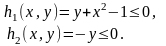
Первое условие теоремы Куна-Таккера позволяет записать два уравнения:

,

.

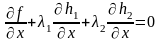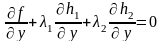Второе условие теоремы позволяет записать еще два уравнения: , .

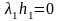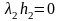Подставляя в них функции 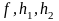и вычислив производные, получаем систему из 4 уравнений с 4 неизвестными:

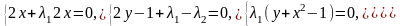
Рассмотрим несколько ветвей решения системы уравнений:

1)

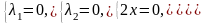
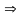
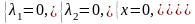
2) .

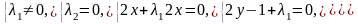
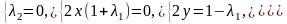Вторая система распадается на два случая:

2а) 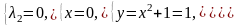; 2б) ;

3) ;

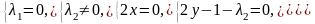
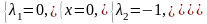4) ,

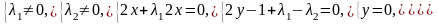Эта система распадается на две

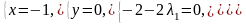
4а) 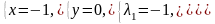; 4б) .

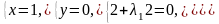
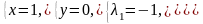После того как система решена результаты собираются в таблицу 15:

Таблица 15

Р	х	у			f
Р1	0		0	0	-
Р2	0	1	-1	0	0
Р3	0	0	0	-1	0
Р4	1	0	-1	-2	1
Р5	-1	0	-1	-2	1

Предварительно убеждаемся, что все точки принадлежат допустимому множеству. Подставляя их координаты в ограничения-неравенства и видя, что они остаются истинными, рассчитываем значение целевой функции в каждой из них. Кроме того, убеждаемся, что третье условие теоремы Куна-Таккера также выполнено во всех точках. Сравнивая значение целевой функции в каждой из найденных точек, видим, что наибольшее значение функции 1 достигается в точках (1;0) и (-1;0), наименьшее - в точке (0; ).