21. Понятие термодинамики как науки. Первый закон термодинамики

Исторически термодинамика возникла в XIX веке в связи с необходимостью изучения закономерностей процессов протекающих в паровых машинах. В настоящее время под технической термодинамикой понимается наука, изучающая процессы взаимного превращения теплоты и работы, а так же физические свойства тел, участвующих в этих преобразования [1].

Основными рабочими телами являются газообразные вещества - газы и пары, которые способны изменять свой объём в зависимости от изменения внешних условий. Рабочее тело в тепловой машине получает или отдаёт теплоту, взаимодействуя с более нагретым или более холодным внешними телами, которые называются источниками теплоты. Источник, который отдаёт теплоту рабочему телу и не изменяет свою температуру, называется верхним источником теплоты (ВИТ), а источник, получающий теплоту от рабочего тела и не изменяющий свою температуру, называется нижним источником теплоты (НИТ).

В зависимости от внешних условий один и тот же газ может находиться в различных состояниях, причём каждое из таких состояний характеризуется конкретными значениями ряда микроскопических величин, называемых термодинамическими параметрами. Это означает, что каждому состоянию газа соответствует одно и только одно значение каждого из термодинамических параметров.

Чтобы однозначно характеризовать состояние газа, необходимо и достаточно задать значения трёх любых его параметров таких, которые имеют конкретный физических смысл и достаточно просто измеряются техническими средствами. Такими термическими параметрами являются абсолютное давление, абсолютная температура и удельный объём. Если эти параметры имеют одинаковые значения по всему объёму рабочего тела, то они называются равновесными.

В основе термодинамики как науки лежат её первый и второй законы, устанавливающие качественные и количественные взаимосвязи между теплотой и механической работой [2].

Первый закон термодинамики устанавливает количественную связь между теплотой и механической энергиями и представляет собой балансовое уравнение изменения энергии в термодинамической системе:

u₂ - u₁ = q – l+ a, (2.1.)

где (u₂ – u₁) - изменение удельной внутренней энергии;

q – удельная теплота c которой тело обменивается энергией с окру

жающей средой;

l – удельная работа по изменению объёма;

a – работа немеханического характера.

К работе немеханического характера можно отнести работу по переносу электрического заряда, работу (теплоту) химического взаимодействия и др.

Если считать, что a = 0, то u₂ – u₁= q – l. В математическом выражении первого закона термодинамики принято подводимую к телу теплоту выражать как функцию внутренней энергии и работы:

q =u₂ - u₁ + l, (2.2)

Тогда первый закон термодинамики с учётом (2.2.) формулируется следующим образом: вся подводимая к телу теплота идёт на изменение внутренней энергии и на совершение работы.

Отметим, что первый закон термодинамики, описывающий эквивалентное превращение теплоты и механической энергии, является частным случаем закона сохранения и превращения энергии, открытого М.В. Ломоносовым.

Из молекулярно-кинетической теории следует, что внутренняя энергия тела пропорциональна его температуре, тогда её изменение будет пропорционально разности температур, т.е.

U₂ – U₁ = c_v (T₂ – T₁) (2.3)

Удельная работа расширения l в уравнении (2.2.) совершается против внешних сил, например расширение газа в цилиндре при постоянном давлении, и аналитически выражается следующим образом:

l = p (v₂ – v₁), (2.4)

где p – полное (абсолютное) давление газа, м³/кг.

С учётом уравнений (2.3) и (2.4) первый закон термодинамики можно представить в развёрнутом виде:

q = c_v (T₂ – T₁)+ p (v₂ – v₁), (2.5)

Уравнение (2.5) часто используется при описании работы теплоэнергетических машин и установок, а так же для анализа типовых термодинамических процессов в газах, которые являются частными случаями первого закона термодинамики.

Теоретически измененные состояния газа полностью характеризуются тремя параметрами p, v и T, при этом теплота либо подводится к газу, либо отводится от него. Такие процессы называются политропными*. Наибольший практический интерес представляют такие процессы, в которых один из основных параметров остаётся постоянным, или процесс осуществляется без теплообмена с окружающей средой. Таких процессов в природе существует четыре:

- изохорный (v = const);

- изобарный (p = const);

- изотермический (T = const);

- адиабатный (dq = 0)

Все процессы при этом рассматриваются как равновесные и обратимые, а их исследование осуществляется на основе уравнения состояния идеального газа и первого закона термодинамики.

Изохорный процесс – это равновесный процесс, протекающий при постоянном объёме (v=const). Такой процесс осуществляется, например, при нагревании или охлаждении газа в замкнутом объёме. Так как в изохорном процессе не происходит изменение объёма, то уравнение первого закона термодинамики (2.5) при (v₂ – v₁) =0 будет иметь следующий вид:

q = c_v (T₂ – T₁), , (2.6)

т.е. в изохорном процессе вся подводимая к телу теплота идёт на изменение его внутренней энергии.

Уравнение (2.6) определяет внутреннюю энергию 1кг газа в изохорном процессе, а его полная внутренняя энергия (m, кг) определяется по уравнению(2.7): Q = c_v m (T₂ – T₁), Дж (2.7)

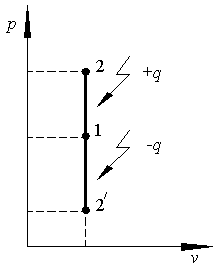
В p – v координатах изохорный процесс изображается вертикальным отрезком (рис.2.1).

На рис. 2.1 процесс изохорного нагревания 1–2, а изохорного охлаждения 1-21. Площадь под линией изохорного процесса равна нулю, что свидетельствует об отсутствии работы. Для построения графика изохорного процесса в T–s координатах используется выражение для энтропии:

Рис. 2.1

ds=c_v , (2.8)

где dq = c_vdT, тогда после интегрировани(2.8) в пределах температур

от T₁ до T₂ получим:

(2.9)

Как следует из выражения (2.9), линия изохорного процесса в T–S координатах являются логарифмической кривой (рис 2.2).