19

25. Закон Архимеда. Остойчивость плавающего тела.

Для проведения кружковой работы по судомоделированию учителю технологии необходимо знать основы теории плавания, уметь определять остойчивость судна в надводном положении и принимать меры по обеспечению необходимой остойчивости и безопасности плавания на воде. Основой теории плавания является закон Архимеда, установленный им 250 лет до н.э.

Из курса физики известно, что закон Архимеда формулируется следующим образом: на тело, погруженное в жидкость, действует выталкивающая сила равная по величине и обратная по направлению силе тяжести жидкости, вытесненной этим телом.

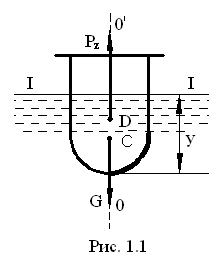
В надводном положении на плавающее тело по оси OZ действуют две силы (рис.1.1).Это сила тяжести тела G и выталкивающая архимедова сила P_z.

Способность тела плавать, т.е. держаться на поверхности при заданной нагрузке, называется плавучестью и определяется по неравенству (1.7): , (1.7) где - суммарная сила тяжести судна и дополнительной загрузки. Отметим, что при подводном

плавании, т.е. в погруженном состоянии . К основным понятиям теории плавания относятся следующие:

- плоскость плавания (I-I) - пересекающая тело плоскость свободной поверхности жидкости;

- ватерлиния – линия пересечения поверхности тела и плоскости плавания;

- осадка (y) – глубина погружения низшей точки тела. Наибольшая допустимая осадка судна отмечается на нём красной ватерлинией;

- водоизмещение – вес воды, вытесненный судном. Водоизмещение судна при полной нагрузке является его основной технической характеристикой;

- центр водоизмещения (точ. D, рис. 1.1) – центр тяжести водоизмещения, через который проходит линия действия выталкивающей архимедовой

силы;

- ось плавания (О О ^' ) – линия проходящая через центр тяжести С и центр водоизмещения D при равновесии тела.

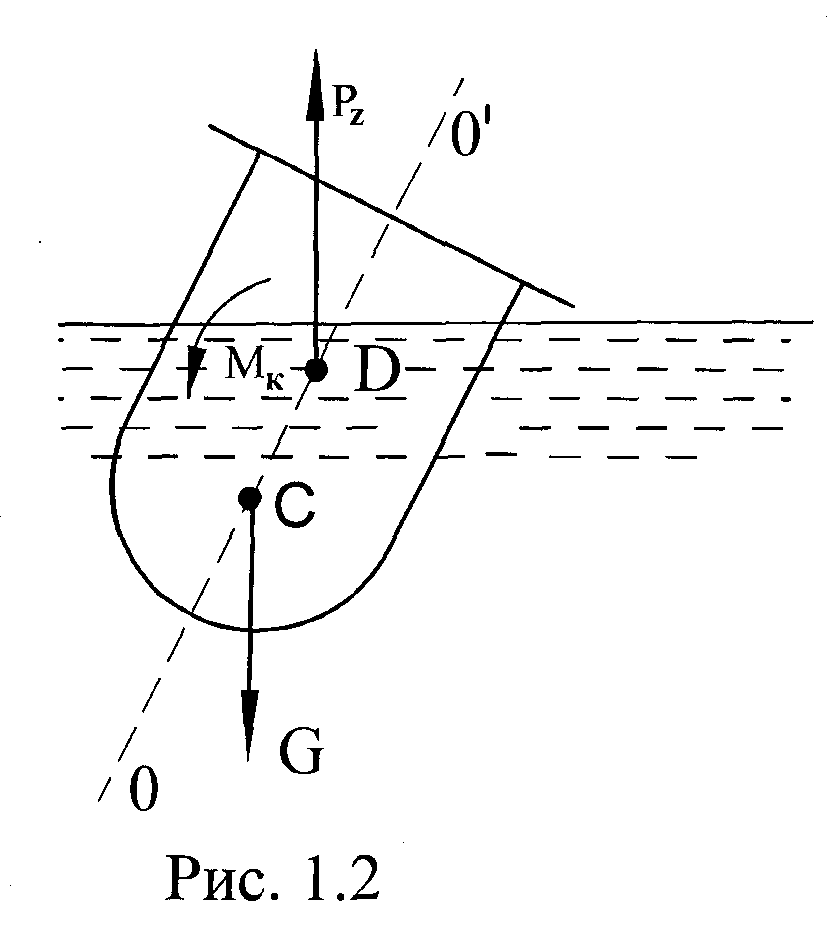
Для сохранения равновесия ось плавления должна быть вертикальна. Если на плавающее судно в поперечном направлении действует внешняя сила, например сила давления ветра, то судно накренится, ось плавания повернётся относительно точки С и возникнет крутящий момент М_к, вращающий судно относительно продольной оси против часовой стрелки (рис.1.2)

После прекращения действия внешней силы судно может вернуться в исходное положение, или опрокинуться в зависимости от его остойчивости.

Остойчивость - способность плавающего тела, выведенного из равновесия, возвращаться в исходное положение после прекращения действия сил вызвавших крен.

Остойчивость плавающего тела зависит от взаимного положения точек С и D. Если центр тяжести С находится ниже центра водоизмещения D, то при надводном плавании тело всегда остойчиво, так как возникающий при крене крутящий момент М_к всегда направлен в сторону противоположную крену.

Если точка С находится выше точки D (рис.1.3), то плавающее тело

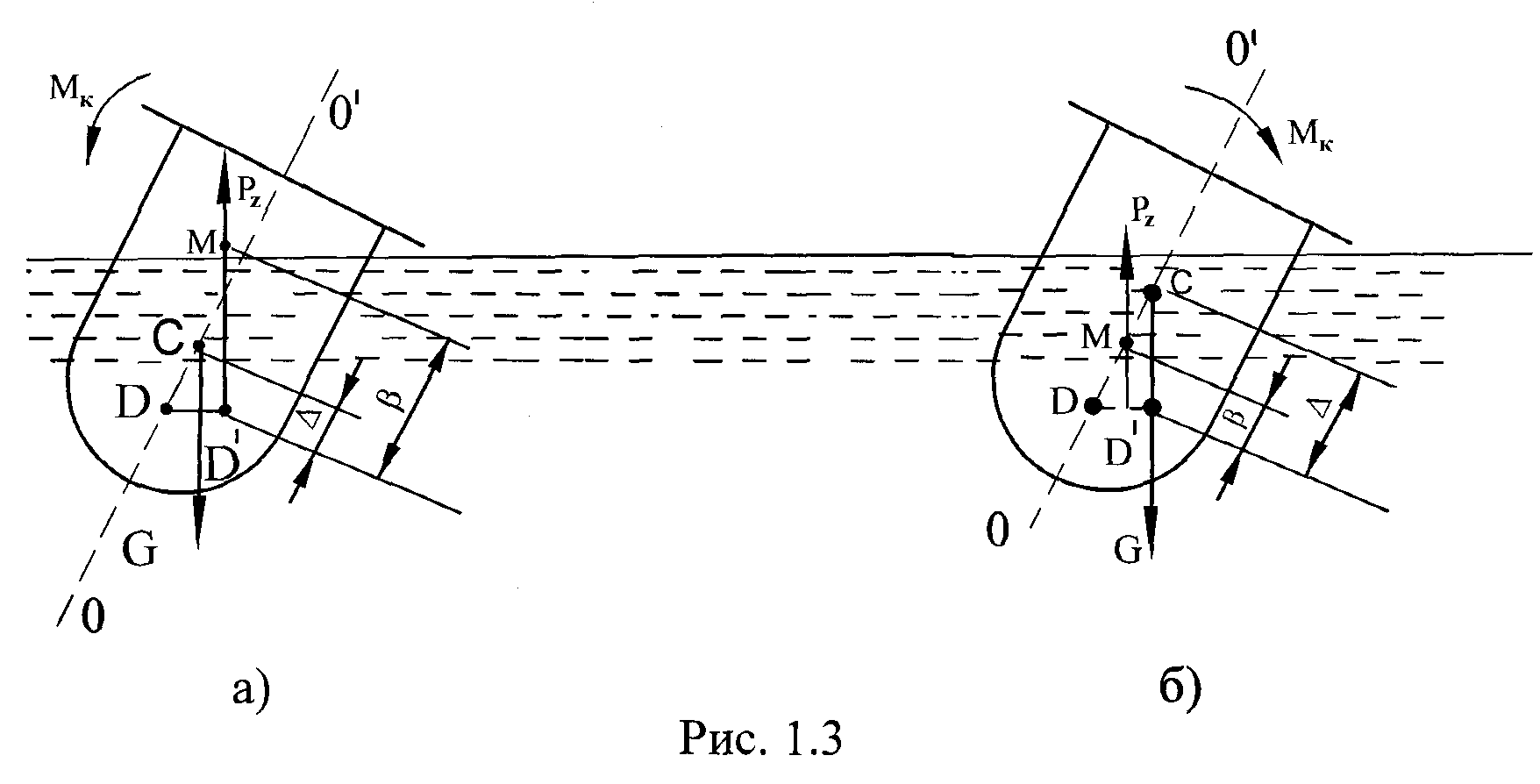
может быть остойчивым и неостойчивым. Рассмотрим эти случаи подробнее. При крене центр водоизмещения D смещается по горизонтали в сторону крена, так как один борт судна вытесняет больший объём воды, чем другой.

Тогда линия действия выталкивающей архимедовой силы P_z пройдёт через новый центр водоизмещения D' и пересечётся с осью плавания ОО' в точке M, называемой метацентром. Для формулирования условия остойчивости обозначаем отрезок M D¹ = , а СD¹ = ,

где  - метацентрический радиус;

• - эксцентриситет.

Условие остойчивости: тело остойчиво, если его метацентрический радиус больше эксцентриситета, т.е.   ..

Графическая интерпретация условия остойчивости представлена на рис. 1.3, из которого видно, что в случае а)   и возникший крутящий момент направлен в сторону противоположную крену, а в случае б) имеем:    и момент М_к вращает тело в сторону крена, т.е. тело не остойчиво.

При решении задач на остойчивость необходимо использовать справочные данные о значениях моментов инерции твёрдых тел относительно горизонтальной оси. При малых углах крена метацентрический радиус  определяется по формуле (1.8):

, (1.8)

где I_c - центральный момент инерции площади ватерлинии относительно оси поворота;

W – объём погруженной части тела.

Центральный момент инерции I_c - определяется по одной из формул таблицы Приложения 2 в зависимости от формы поперечного сечения плавающего тела.