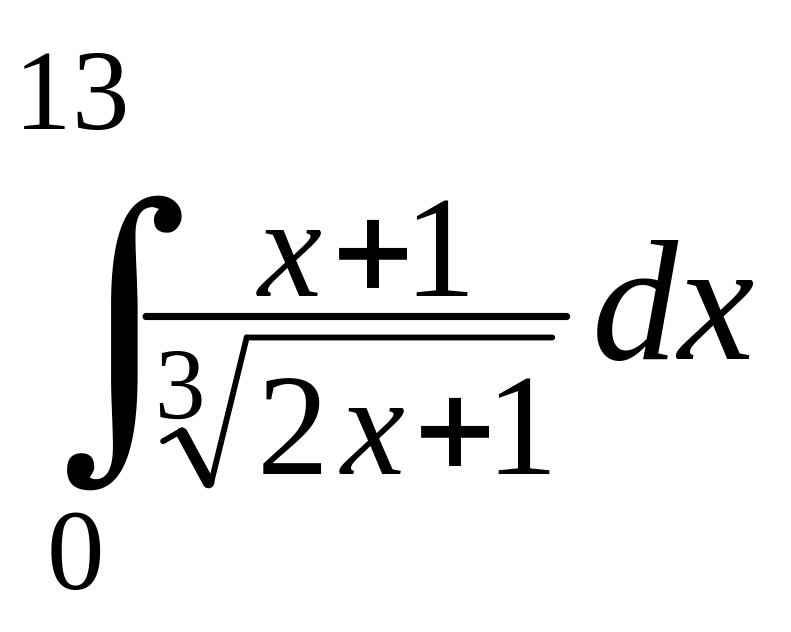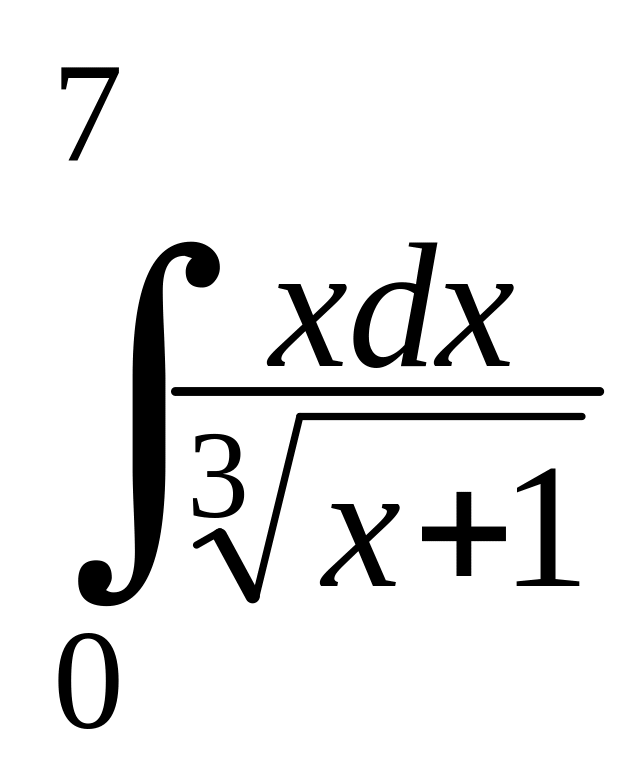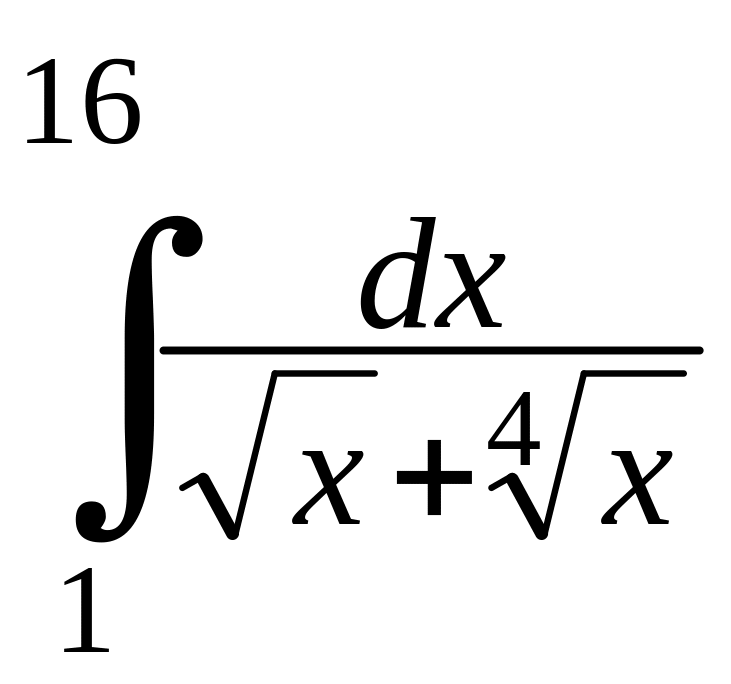- •Раздел 4. Интеграл и его приложения (Контрольная работа n 4)
- •§4.1. Неопределенный интеграл
- •4.1.1. Первообразная и неопределенный интеграл
- •4) Если то
- •4.1.2. Интегрирование с помощью замены переменной
- •4.1.3. Интегрирование по частям
- •4.1.4. Интегрирование рациональных дробей
- •4.1.5. Интегрирование тригонометрических функций
- •§4.2. Определенный интеграл
- •§4.3 Несобственные интегралы
- •§4.4 Приложения определенных интегралов
- •4.4.1. Вычисление площади плоской фигуры
- •4.4.2. Вычисление длины дуги плоской кривой
- •§4.5. Задания к контрольной работе n 4
§4.5. Задания к контрольной работе n 4
Задание 4.1. Найти неопределенные интегралы.
4.1.0. |
а) |
б) |
|
в) |
г) |
4.1.1. |
а) |
б) |
|
в) |
г) |
4.1.2. |
а) |
б) |
|
в) |
г) |
4.1.3. |
а) |
б) |
|
в) |
г) |
4.1.4. |
а) |
б) |
|
в) |
г) |
4.1.5. |
а) |
б) |
|
в) |
г) |
4.1.6. |
а) |
б) |
|
в) |
г) |
4.1.7. |
а) |
б) |
|
в)
|
г) |
4.1.8. |
а) |
б) |
|
в) |
г) |
4.1.9. |
а) |
б) |
|
в) |
г) |
Задание 4.2. Вычислить определенные интегралы.
4.2.0. |
|
|
4.2.5. |
|
4.2.1. |
|
|
4.2.6. |
|
4.2.2. |
|
|
4.2.7. |
|
4.2.3. |
|
|
4.2.8. |
|
4.2.4. |
|
|
4.2.9. |
|
Задание 4.3. Вычислить несобственный интеграл или доказать его расходимость.
4.3.0. |
|
|
4.3.5. |
|
4.3.1. |
|
4.3.6. |
|
|
4.3.2. |
|
4.3.7. |
|
|
4.3.3. |
|
4.3.8. |
|
|
4.3.4. |
|
4.3.9. |
|
Задание 4.4. Вычислить площади фигур, ограниченных заданными линиями.
4.4.0. |
|
4.4.1. |
|
4.4.2. |
|
4.4.3. |
|
4.4.4. |
|
4.4.5. |
|
4.4.6. |
|
4.4.7. |
|
4.4.8. |
|
4.4.9. |
|
94 95