4.1.5. Интегрирование тригонометрических функций
При
интегрировании тригонометрических
функций часто используют универсальную
тригонометрическую подстановку:
В результате этой подстановки имеем:
Исходный интеграл приводится к интегралу от рациональной дроби.
Пример
4.20.
Найти
интеграл
.
Решение. Используем универсальную тригонометрическую подстановку.
.
Возвращаясь к переменной x, получим
.
Универсальная тригонометрическая подстановка во многих случаях приводит к сложным вычислениям. Поэтому в некоторых частных случаях интегрирование может быть упрощено.
1)
Если подынтегральная функция является
нечетной функцией относительно
,
то удобно применять подстановку
2)
Если подынтегральная функция является
нечетной функцией относительно
то применяют подстановку
3)
Если подынтегральная функция является
четной относительно
и
то применяют подстановку
Пример
4.21.
Найти
интеграл
.
Решение. Преобразуем подынтегральную функцию.
.
Полученная
дробь является нечетной функцией
относительно
поэтому удобно воспользоваться
подстановкой:
.
.
Возвращаясь к переменной х, получим
.
§4.2. Определенный интеграл
Пусть
функция
определена на отрезке
,
– некоторое разбиение отрезка
на части
,
и
,
,...,
– некоторый набор точек. Положим
.
.
Определенным
интегралом
называется предел интегральных сумм
если
он существует и конечен и не зависит от
выбора разбиения отрезка
на
части и выбора точек
.
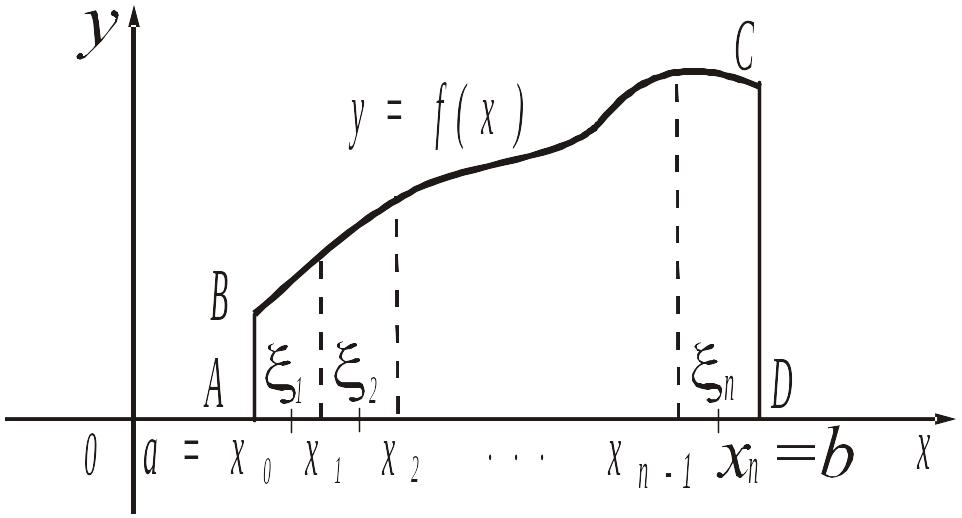
Рис. 23.
Известно, что если функция непрерывна на отрезке , то
существует.
Геометрический
смысл определенного интеграла для
случая
:
площадь криволинейной трапеции ABCD
(рис. 23).
Свойства определенного интеграла
;
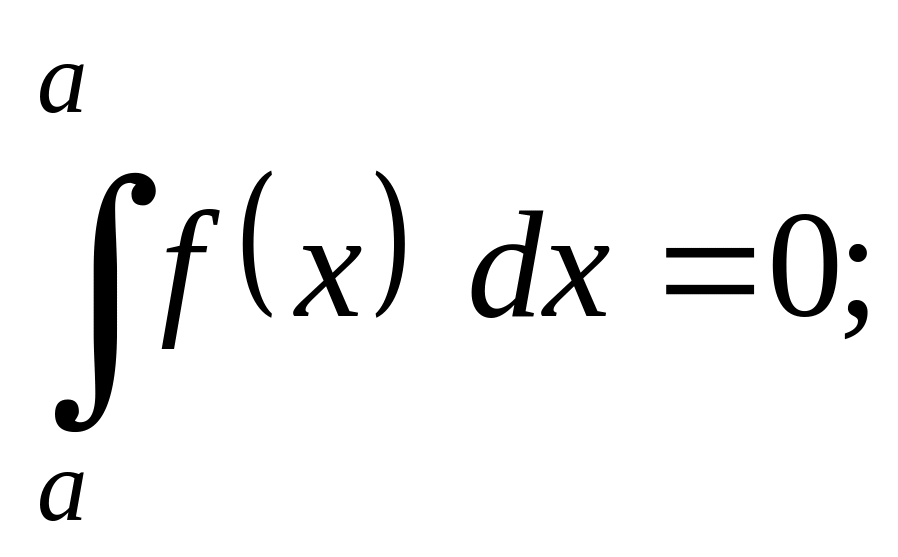
4.
.
Правила вычисления определенного интеграла
1.
Формула Ньютона-Лейбница. Если
– некоторая первообразная функции
то
2.
Формула замены переменной. Если
– монотонная непрерывно дифференцируемая
для
функция, такая, что
,
то
Замечание. При замене переменной в определенном интеграле меняются и пределы интегрирования.
3. Формула интегрирования по частям
.
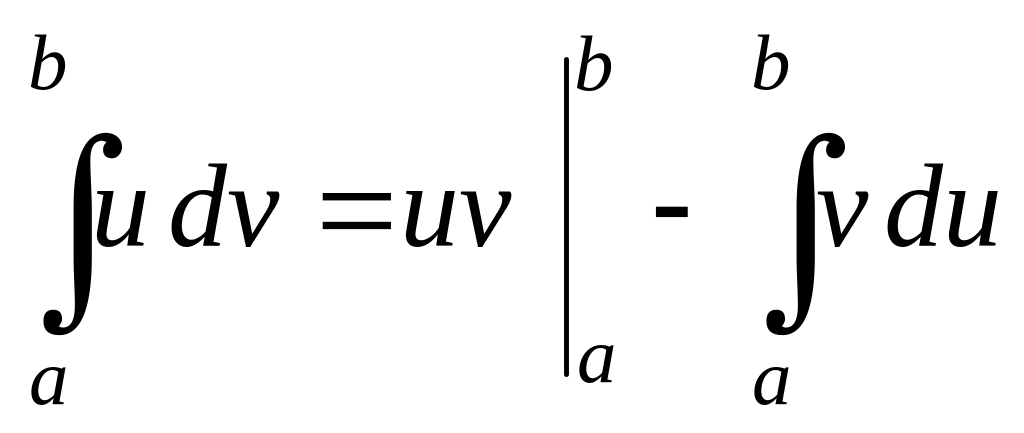Пример
4.22.
Вычислить
интеграл
.
Решение. Сделаем замену переменной:
,
,
Для пределов интегрирования имеем:
если
,
то
;
если
,
то
.
.
Пример
4.23.
Вычислить
интеграл
.
Решение.
Применим формулу интегрирования по
частям. Пусть
,
,
тогда
,
.
.
§4.3 Несобственные интегралы
Несобственными интегралами называются интегралы с бесконечными пределами и интегралы от неограниченных функций.
Несобственные интегралы с бесконечными пределами
По определению
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; в противном случае – расходящимся.
Аналогично определяется интеграл
.
Несобственный интеграл с двумя бесконечными границами определяется формулой
,
где с – любая фиксированная точка оси х.
Таким
образом, интеграл
сходится только тогда,
когда сходится каждый из интегралов
и
.
Если хотя бы один из этих интегралов
расходится, то расходится и интеграл
.
Несобственные интегралы от неограниченных функций
Если
функция
имеет бесконечный разрыв в точке
,
то есть
и
непрерывна при
,
то по определению
,
.
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; в противном случае – расходящимся.
Если
и
непрерывна при
,
то
,
.
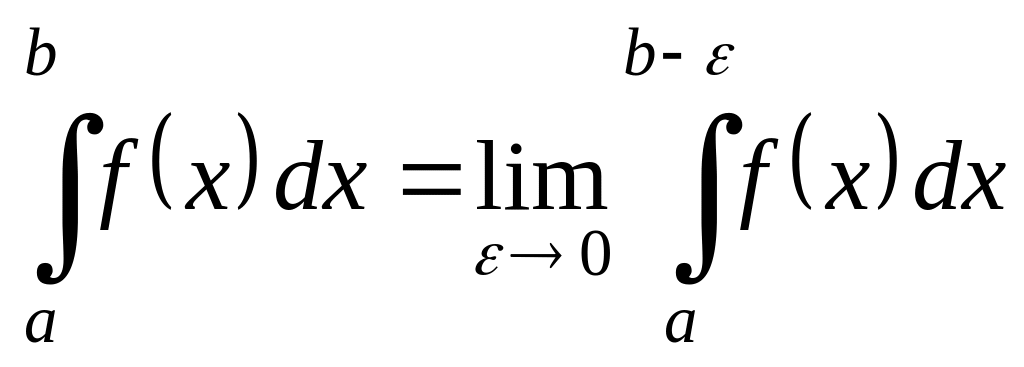Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; в противном случае – расходящимся.
Если
,
и непрерывна при
и
,
то
,
.
Пример 4.24. Вычислить интеграл или доказать его расходимость:
Решение.
.
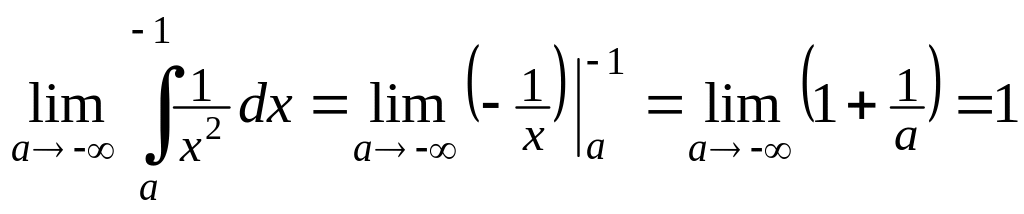Несобственный интеграл сходится.
Пример 4.25. Вычислить интеграл или доказать его расходимость:
Решение.
.
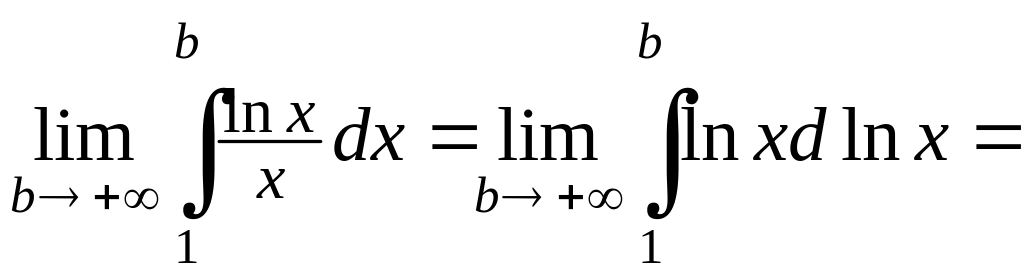
Несобственный интеграл расходится.
Пример 4.26. Вычислить интеграл или доказать его расходимость:
Решение.
Подынтегральная функция
в точке
имеет бесконечный разрыв, поэтому
.
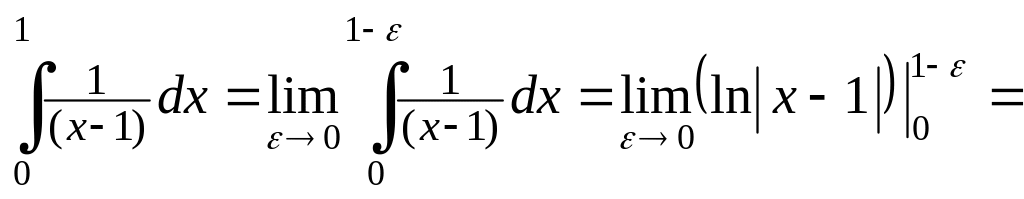
Несобственный интеграл расходится.
Пример 4.27. Вычислить интеграл или доказать его расходимость:
Решение.
.
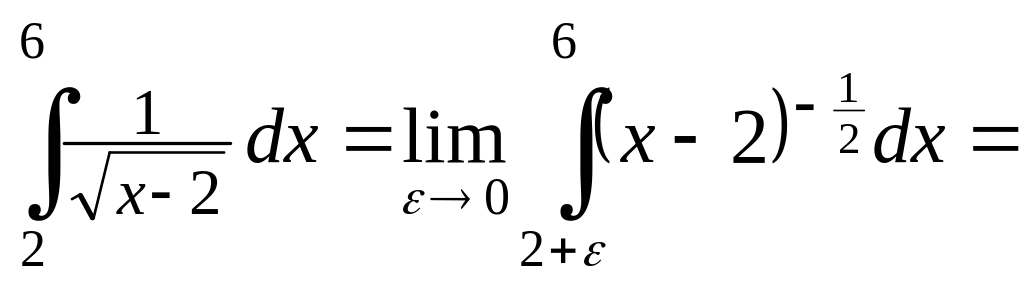
Данный интеграл сходится.