18.Алгоритмы распознавания общезначимости формул в частных случаях.
Формула А называется выполняемой области М если существует значения переменных при которых А принимает истинное значение.
А называется выполняемой если существует область на которой эта формула выполнима.
А
называется ТИ в области М если принимает
истинные значения для всех значений
переменного (т е на все А называется
общезначимой если она
ТИ на всякой области.
А ТЛ в области М если она принимает логичные значения для всех переменных.
Общезначимые формулы называются логическим законом.
19. Примечание языка логики предикатов для записи математических предложений.
Логический квадрат
Систему взаимоотношений между универсальными и экзистенциальными высказываниями возникающими при определении операций взятия квантора общности и квантора существования. Схематично представляют в виде логического квадрата
Высказывание
и
-
не могут быть не для какого предиката
Р(х) одновременно истинными (хотя могут
быть одновременно ложными). Их называют
контрарными.
Высказывание
и
не могут быть не для какого предиката
Р(х) одновременно ложными (но могут быть
одновременно истинными). Их называют
субконтрарными.
Те высказывания, стоящие в вершинах каждой диагонали квадрата противоречат одно другому.
Под каждым из универсальных высказываний, стоящих в вершинах стоит высказывание следующего из него, то импликация этих высказываний являются истинной.
20. Замечания об аксиоматическом исчислении предикатов.
1. Определение формулы исчисление предикатов совпадает с определением формулы логики предиката.
2. Выбор системы аксиом может осуществляться по-разному (можно выбрать 11 аксиом так же как и в ИВ, и добавить след. аксиомы:
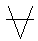х
(F(x)→F(y))F(t) →
х F(x), где t- не содержит переменных х
3. К правилам вывода которые использовались в ИВ добавляются ещё 2 правила:
Правило введения квантора общности
F→G(x)
F→ x(G(x))
правило введения квантора существования
G(x)→F
х G(x)→F
( в случаи если F не зависит от х)
4. Понятие вывода и доказуемой формулы, определяется так же как и в ИВ
5. Рассматриваются проблемы: разрешимости, непротиворечивости, полноты, независимости.