15. Значение формулы логики предикатов.

О логическом значении формулы логики предикатов можно говорить лишь тогда, когда задано множество M, на котором определены входящие в эту формулу предикаты. Логическое значение формулы логики предикатов зависит от значений трёх видов переменных: 1) значений входящих в формулу переменных высказываний, 2) значений свободных предметных переменных из множества М, 3) значений предикатных переменных.

При конкретных значениях каждого из трёх видов переменных формула логики предикатов становится высказыванием, имеющим истинное или ложное значение.

В качестве примера рассмотрим формулу , (1) в которой двухместный предикат Р(x, y) определён на множестве MхM, где M={0,1,2,…,n,…}, т.е. MхM=NхN.

В формулу (1) входит переменный предикат P(x,y), предметные переменные x,y,z, две из которых y и z – связанные кванторами, а x – свободная.

Возьмём за конкретное значение предиката P(x,y) фиксированный предикат P⁰(x,y): “x<y”, а свободной переменной х придадим значение . Тогда при значениях y, меньших x⁰=5, предикат P⁰(x⁰,y) принимает значение “ложь”, а импликация при всех принимает значение “истина”, т.е. высказывание имеет значение “истина”.

16. Равносильные формулы логики предикатов.

Определение 1.

Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесённых к области М.

Определение 2.

Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.

Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей.

Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, не содержащая х). Тогда имеют место равносильности:

1.

2.

3.

4.

5.

6. .

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

Равносильность 1 означает тот простой факт, что, если не для всех х истинно А(х), то существует х, при котором будет истиной .

Равносильность 2 означает тот простой факт, что, если не существует х, при котором истинно А(х), то для всех х будет истиной .

Равносильности 3 и 4 получаются из равносильностей 1 и 2, соответственно, если от обеих их частей взять отрицания и воспользоваться законом двойного отрицания.

17.Предваренная нормальная форма (пнф)

Формула логики предикатов имеет нормальную форму если она содержит только операции. ( )

ПНФ – это такая форма где кванторные операции отсутствуют, либо используются после всех операция. Т.е.

Теорема: все формулы логики предикатов (ЛП) м/б приведены к ПНФ

Доказательство: пусть формула имеет нормальную форму.

Если формула элементарная => она квадратов не содержит => она сама по себе является в ПНФ.

1. Пусть формула A содержит k+1 операцию и , где L(x) – cодержит к-операций изходя из условия L(x) находиться в пнф. Поскольку кванторы записаны впереди данной формулы то A находиться в пнф.

2. Пусть A=L где L находиться в ПНФ тогда с помощью равносильностей

1 и 2 отрицание можно внести под знак кванторов, тогда А будет в пнф

3. Пусть А=L1 V L2; где L1 L2 в пнф. Переименуем в L2 связанные предметные переменные так, чтобы они были различными.

Используя равносильности 7 и 1

Запишем формула А используя формулу L2 под знаки квантора: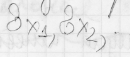

Получается что

Далее ведем под знаки кванторов

формулу L1.

Получаем:

Т.о А находиться в ПНФ