
- •Жаппай қызмет ету жүйелері туралы жалпы мәліметтер (жқж).
- •Оқиғалар ағынының түрлері, ағыны ж/е қасиеттері.
- •Жқж модельдерінің символдық белгіленуі (Кендалл бойынша).
- •Қызмет ету процессі Марков процессі ретінде. Колмогоров-Чепмен теңдеуі.
- •Күтуі бар бірарналы жқж. Колмогоров теңдеулерін құрудың жалпы заңы.
- •Жойылудың және көбеюдің сұлбасы. Литтл формуласы.
- •11. Қарсылықты бірарналы жқж
- •12. Қабыл алмауы бар бірарналы жқж.
- •13. Шектелген кезегі бар бірарналы жқж.
- •17. Көпканалды өзара жәрдеммен жұмыс істейтін жқж
- •18. Тұйық жқж. Ауысулар графы мен сипаттамалары. Мысал. Тұйық жқж
- •20. Имитациялық моделдеу тіліе құру негіздері. Имитациялық модельдеу тілінің объектілері, олардың құрамы және блоктары.
- •21. Gpss World туралы жалпы мәліметтер. Gpss – блоктардың форматы. Gpss World тілінде бірканалды құрылғыларды модельдеу.
- •24. Terminatе блогы. Start операторы.
- •25. Gpss World тілінің диалогтық мүмкіндіктері
- •29. Стандартты сандық атрибуттар (сса). Сса транзакт және блоктар үшін. (Этот вопрос смотреть дополнительно на русском)
- •30. Модельдегі транзактардың жылжу маршрутын өзгерту. Displace, transfer, loop блоктары
- •32. ) Безусловный режим выбора в блоке transfer
- •34. Transfer блогындағы таңдаудың статистикалық режимі
- •37. Plus, index және mark блоктары
- •39. Логикалық және буль операторлары, қатынастар операторлары.
- •41. Gpss-тағы функциялар. Функцияны суреттейтін оператор.
- •43. Generate және advance блоктарында функцияларды қолдану
- •Generate a, b advance a, b
- •44. Имитациялық модельде статистиканы жинау әдісі
- •46. Псевдокездейсоқ сандардың генераторлары
- •47.Арифметикалық айнымалылар және арифметикалық белгілер
- •48. Storage және function блогі
- •49. Table және tabulate блоктары
- •50.Priority және sabevalue блогы
Күтуі бар бірарналы жқж. Колмогоров теңдеулерін құрудың жалпы заңы.
Кірісінде
интенсивтілікті қарапайым ағынды
қамтитын және
 көрсеткішті қызмет көрсетудің
экспоненциалды уақытына ие бір каналдық
жүйе жұмысын қарастырайық.
көрсеткішті қызмет көрсетудің
экспоненциалды уақытына ие бір каналдық
жүйе жұмысын қарастырайық.
 — жүйе күйі (онда n
тапсырыс бар).
— жүйе күйі (онда n
тапсырыс бар).
 уақыт сәтінде
уақыт сәтінде
 ықтималдықты бір тапсырыс келуі мүмкін,
ықтималдықты бір тапсырыс келуі мүмкін,
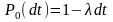 ықтималдықты нөл тапсырыс келуі де
мүмкін, мүмкін
ықтималдықты нөл тапсырыс келуі де
мүмкін, мүмкін
 ықтимаклдықты бір тапсырысқа қызмет
көрсетілуі мүмкін, мүмкін
ықтимаклдықты бір тапсырысқа қызмет
көрсетілуі мүмкін, мүмкін
 ықтималдықпен бір де бір тапсырысқа
қызмет көрсетілмеуі де.
ауысулар
матрицасыны келесі түрде көрсетілетін
болады:
ықтималдықпен бір де бір тапсырысқа
қызмет көрсетілмеуі де.
ауысулар
матрицасыны келесі түрде көрсетілетін
болады:




·
·
·
·
·
·
·



 ықтималдығы
ықтималдығы
 уақытында тапсырыс келіп түспеуі
ықтималдығымен анықталады.
уақытында тапсырыс келіп түспеуі
ықтималдығымен анықталады.
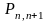 ықтималдығы бір тапсырыстың
ықтималдығы бір тапсырыстың
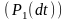 келу ықтималдығымен анықталады, ал
келу ықтималдығымен анықталады, ал
 ықтималдығы бір тапсырысқа
қызмет көрсету ықтималдығымен анықталады.
ықтималдығы бір тапсырысқа
қызмет көрсету ықтималдығымен анықталады.
 ықтималдығы құрамдас оқиғалар
ықтималдығымен анықталады: тапсырыс
келмейді және қызмет көрсетілмейді.
ықтималдығы құрамдас оқиғалар
ықтималдығымен анықталады: тапсырыс
келмейді және қызмет көрсетілмейді.
Ауысу матрицаксын ықшамдырақ түрде, ауысулар графы түрінде көрсетуге болады, ондағы төбелер жүйе күйін білдіреді, ал доғалары – ауысулар ықтималдықтарын белгілейтін болады:
...

Ауысулар графынан ықтималдық күйлер үшін дифференциалдық теңдеулер алынуы мүмкін, ол Колмогоров теңдеуі деп аталады.
Колмогоров теңдеулерін құрудың жалпы заңы.
Теңдеудің сол жағында
 -ші
күйдің туынды ықтималдығы тұр, оң жағында
— барлық күйлер ықтималдықтары
туындысының қосынды шамасы (осы күйлерден
шыққан бағыттауыш сызықтары оқиғалардың
сәйкес ағындарының интенсивтілігіне
бағытталады, минус жүйені бір күйден
шығаратын барлық ағындардың қосынды
интенсивтілігі берілген күйдің (
-ші)
ықтималдығына көбейтілген.
-ші
күйдің туынды ықтималдығы тұр, оң жағында
— барлық күйлер ықтималдықтары
туындысының қосынды шамасы (осы күйлерден
шыққан бағыттауыш сызықтары оқиғалардың
сәйкес ағындарының интенсивтілігіне
бағытталады, минус жүйені бір күйден
шығаратын барлық ағындардың қосынды
интенсивтілігі берілген күйдің (
-ші)
ықтималдығына көбейтілген.
Осы ереже бойынша дифференциалдық теңдеулер жүйесін құрамыз:
 ,
,
 ,
,
. . .

Түрлендіргеннен кейін алатынымыз:
 ,
,
 ,
,
. . .
 .
.
Бұл теңдеулер бастапқы ережелер берілген жағдайда шешілуі мүмкін:
 ,
,
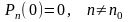 ,
,
Лаплас түрлендіруін пайдаланып жиілікті тәсілмен.
Қалыптасқан немесе стационарлық режимге жиі қызығушылық туындайды, ол үшін мына теңдік дұрыс
 .
.
Бұл жағдайда дифференциалдық теңдеулер жүйесі сызықтық теңдеулер жүйесіне түрленеді:
 ,
,
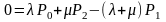 ,
,
. . .
 ,
,
бұдан
 ,
,
 ,
,
 .
.
 екенін
ескеріп, мынаны аламыз
екенін
ескеріп, мынаны аламыз

 ,
,

 парамері жүйедегі қанықтылық
дәрежесін білдіреді және жүктеме немесе
ЖҚКЖ-н пайдалану коэффициенті деп
аталады. Бірканалдық ЖҚКЖ-і үшін
парамері жүйедегі қанықтылық
дәрежесін білдіреді және жүктеме немесе
ЖҚКЖ-н пайдалану коэффициенті деп
аталады. Бірканалдық ЖҚКЖ-і үшін
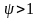 кезінде қалыптасқан режим деген болмайды,
кезек шексіз өсе береді..
кезінде қалыптасқан режим деген болмайды,
кезек шексіз өсе береді..
Қалыптасқан режим бастапқы шарттарға байланысты емес. Қалыптасқан режимнің кейбір сандық сипаттамаларын аламыз.
Жүйедегі тапсырыстардың орташа саны:
 .
.
Бос емес каналдардың орташа саны:

Кезектегі тапсырыстардың орташа саны:
 ,
,
қарапайымырақ:
 .
.
Күтуі қамтитын бірарналы ЖҚЖ негізгі сипаттамалары. Кірісінде интенсивтілікті қарапайым ағынды қамтитын және көрсеткішті қызмет көрсетудің экспоненциалды уақытына ие бір каналдық жүйе жұмысын қарастырайық. — жүйе күйі (онда n тапсырыс бар). уақыт сәтінде ықтималдықты бір тапсырыс келуі мүмкін, ықтималдықты нөл тапсырыс келуі де мүмкін, мүмкін ықтимаклдықты бір тапсырысқа қызмет көрсетілуі мүмкін, мүмкін ықтималдықпен бір де бір тапсырысқа қызмет көрсетілмеуі де. ауысулар матрицасыны келесі түрде көрсетілетін болады:
·
·
·
·
·
·
·
ықтималдығы уақытында тапсырыс келіп түспеуі ықтималдығымен анықталады. ықтималдығы бір тапсырыстың келу ықтималдығымен анықталады, ал ықтималдығы бір тапсырысқа қызмет көрсету ықтималдығымен анықталады. ықтималдығы құрамдас оқиғалар ықтималдығымен анықталады: тапсырыс келмейді және қызмет көрсетілмейді.
Ауысу матрицаксын ықшамдырақ түрде, ауысулар графы түрінде көрсетуге болады, ондағы төбелер жүйе күйін білдіреді, ал доғалары – ауысулар ықтималдықтарын белгілейтін болады:
...
Ауысулар графынан ықтималдық күйлер үшін дифференциалдық теңдеулер алынуы мүмкін, ол Колмогоров теңдеуі деп аталады.
Жүйедегі тапсырыстардың орташа саны:
.
Бос емес каналдардың орташа саны:
Кезектегі тапсырыстардың орташа саны:
,
қарапайымырақ:
.
