
- •Многоугольные области: а - ограниченное множество; б - пустое множество; в - неограниченное множество
- •1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
- •2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
- •3. Проводим модификацию матрицы. Вычеркиваем строки и столбцы с возможно большим количеством нулевых элементов:
- •1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
- •2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
- •4. Методом проб и ошибок определяем матрицу назначения х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить минимальную стоимость назначения.
- •1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
- •2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
4. Методом проб и ошибок определяем матрицу назначения х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить минимальную стоимость назначения.
M |
1 |
[-0-] |
[0] |
[-0-] |
1 |
2 |
M |
[0] |
1 |
1 |
[-0-] |
1 |
[0] |
M |
[-0-] |
[-0-] |
[-0-] |
2 |
[-0-] |
2 |
M |
2 |
[0] |
[0] |
2 |
[-0-] |
[-0-] |
M |
[-0-] |
[-0-] |
2 |
1 |
1 |
[0] |
M |
Cmin = 5 + 4 + 3 + 1 + 2 + 6 = 21
Путь: (1;4), (2;3), (3;2), (4;6), (5;1), (6;5)
Альтернативный вариант №2.
M |
1 |
[0] |
[-0-] |
[-0-] |
1 |
2 |
M |
[-0-] |
1 |
1 |
[0] |
1 |
[-0-] |
M |
[0] |
[-0-] |
[-0-] |
2 |
[0] |
2 |
M |
2 |
[-0-] |
[0] |
2 |
[-0-] |
[-0-] |
M |
[-0-] |
[-0-] |
2 |
1 |
1 |
[0] |
M |
Cmin = 5 + 4 + 1 + 3 + 2 + 6 = 21
Путь: (3;4), (1;3), (2;6), (4;2), (5;1), (6;5)
Задание 5.
![]()
Решение:
В качестве показателей эффективности
СМО с отказами будем рассматривать:
А
— абсолютную пропускную способность
СМО, т.е. среднее число заявок, обслуживаемых
в единицу времени;
Q — относительную
пропускную способность, т.е. среднюю
долю пришедших заявок, обслуживаемых
системой;
Pотк. — вероятность
отказа, т.е. того, что заявка покинет СМО
необслуженной;
![]() — среднее число занятых каналов (для
многоканальной системы).
Одноканальная
система с отказами . Рассмотрим задачу.
Имеется один канал, на который
поступает поток заявок с интенсивностью
λ. Поток обслуживаний имеет интенсивность
μ1. Найти предельные вероятности
состояний системы и показатели ее
эффективности.
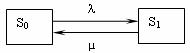
Система S (СМО) имеет
два состояния: S0 — канал свободен,
S1 — канал занят. Размеченный граф
состояний представлен на рис.
— среднее число занятых каналов (для
многоканальной системы).
Одноканальная
система с отказами . Рассмотрим задачу.
Имеется один канал, на который
поступает поток заявок с интенсивностью
λ. Поток обслуживаний имеет интенсивность
μ1. Найти предельные вероятности
состояний системы и показатели ее
эффективности.
Система S (СМО) имеет
два состояния: S0 — канал свободен,
S1 — канал занят. Размеченный граф
состояний представлен на рис.
 В
предельном, стационарном режиме система
алгебраических уравнений для вероятностей
состояний имеет вид.
В
предельном, стационарном режиме система
алгебраических уравнений для вероятностей
состояний имеет вид.
![]()
![]() т.е.
система вырождается в одно уравнение.
Учитывая нормировочное условие p0+p1=1,
найдем из (18) предельные вероятности
состояний
т.е.
система вырождается в одно уравнение.
Учитывая нормировочное условие p0+p1=1,
найдем из (18) предельные вероятности
состояний
![]() которые выражают среднее относительное
время пребывания системы в состоянии
S0 (когда канал свободен) и S1
(когда канал занят), т.е. определяют
соответственно относительную пропускную
способность Q системы и вероятность
отказа Pотк.
которые выражают среднее относительное
время пребывания системы в состоянии
S0 (когда канал свободен) и S1
(когда канал занят), т.е. определяют
соответственно относительную пропускную
способность Q системы и вероятность
отказа Pотк.
Имеем:
Ро=0,5 (по условию)
Р1=1-Ро=1-0,5=0,5
Тогда
![]() Решая
эту систему, видим, что λ=μ
Решая
эту систему, видим, что λ=μ
Задание 6.
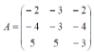
Решение:
Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков.
Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называют выбором стратегии игрока.
Если каждый из игроков выбрал свою стратегию, то эту пару стратегий называют ситуацией игры. Следует заметить, каждый игрок знает, какую стратегию выбрал его противник, т.е. имеет полную информацию о результате выбора противника.
Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.
