
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •1. Проверка критерия оптимальности.
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •4. Пересчет симплекс-таблицы.
- •1. Проверка критерия оптимальности.
1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
Базис |
В |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
x11 |
x12 |
x4 |
4.62 |
0 |
0 |
0 |
1 |
-0.62 |
-0.46 |
0 |
-1.31 |
0 |
0 |
1.31 |
0 |
x9 |
29.27 |
0 |
0 |
0 |
0 |
0.23 |
-0.0769 |
0 |
0.62 |
1 |
0 |
-0.62 |
-1 |
x7 |
33.65 |
0 |
0 |
0 |
0 |
-0.15 |
0.38 |
1 |
0.92 |
0 |
-1 |
-0.92 |
0 |
x1 |
123.65 |
1 |
0 |
0 |
0 |
-0.15 |
0.38 |
0 |
0.92 |
0 |
0 |
-0.92 |
0 |
x2 |
70 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
x3 |
89.27 |
0 |
0 |
1 |
0 |
0.23 |
-0.0769 |
0 |
0.62 |
0 |
0 |
-0.62 |
0 |
F(X6) |
20148.46 |
0 |
0 |
0 |
0 |
1.54 |
26.15 |
0 |
40.77 |
0 |
M |
-40.77+M |
M |
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.
Оптимальный план можно записать так:
x1 = 123.65
x2 = 70
x3 = 89.27
F(X) = 80*123.65 + 70*70 + 60*89.27 = 20148.46
Видим, что при увеличении дефицитных ресурсов, значение целевой функции выросло на:
20148,46-19075=1073,46 ден.ед.
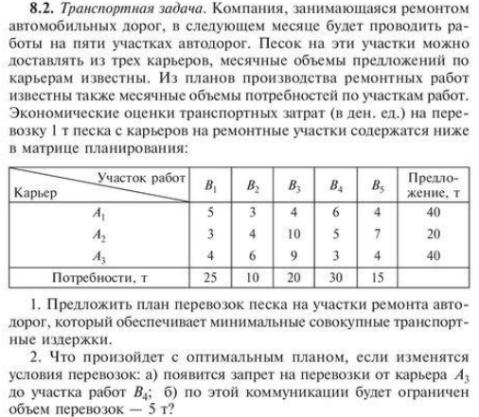
Решение:
Математическая модель транспортной задачи:
F = ∑∑cijxij, (1)
при условиях:
∑xij = ai, i = 1,2,…, m, (2)
∑xij = bj, j = 1,2,…, n, (3)
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5 |
3 |
4 |
6 |
4 |
40 |
2 |
3 |
4 |
10 |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
3 |
4 |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
|
Проверим необходимое и достаточное условие разрешимости задачи.
∑a = 40 + 20 + 40 = 100
∑b = 25 + 10 + 20 + 20 + 15 = 90
Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 10 (100—90). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.
Занесем исходные данные в распределительную таблицу.
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5 |
3 |
4 |
6 |
4 |
0 |
40 |
2 |
3 |
4 |
10 |
5 |
7 |
0 |
20 |
3 |
4 |
6 |
9 |
3 |
4 |
0 |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
Этап I. Поиск первого опорного плана.
1. Используя метод северо-западного угла, построим первый опорный план транспортной задачи.
План начинается заполняться с верхнего левого угла.
Искомый элемент равен 5
Для этого элемента запасы равны 40, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(40,25) = 25.
5 |
3 |
4 |
6 |
4 |
0 |
40 - 25 = 15 |
x |
4 |
10 |
5 |
7 |
0 |
20 |
x |
6 |
9 |
3 |
4 |
0 |
40 |
25 - 25 = 0 |
10 |
20 |
20 |
15 |
10 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 15, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x12 = min(15,10) = 10.
5 |
3 |
4 |
6 |
4 |
0 |
15 - 10 = 5 |
x |
x |
10 |
5 |
7 |
0 |
20 |
x |
x |
9 |
3 |
4 |
0 |
40 |
0 |
10 - 10 = 0 |
20 |
20 |
15 |
10 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 20. Поскольку минимальным является 5, то вычитаем его.
x13 = min(5,20) = 5.
5 |
3 |
4 |
x |
x |
x |
5 - 5 = 0 |
x |
x |
10 |
5 |
7 |
0 |
20 |
x |
x |
9 |
3 |
4 |
0 |
40 |
0 |
0 |
20 - 5 = 15 |
20 |
15 |
10 |
0 |
Искомый элемент равен 10
Для этого элемента запасы равны 20, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x23 = min(20,15) = 15.
5 |
3 |
4 |
x |
x |
x |
0 |
x |
x |
10 |
5 |
7 |
0 |
20 - 15 = 5 |
x |
x |
x |
3 |
4 |
0 |
40 |
0 |
0 |
15 - 15 = 0 |
20 |
15 |
10 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 5, потребности 20. Поскольку минимальным является 5, то вычитаем его.
x24 = min(5,20) = 5.
5 |
3 |
4 |
x |
x |
x |
0 |
x |
x |
10 |
5 |
x |
x |
5 - 5 = 0 |
x |
x |
x |
3 |
4 |
0 |
40 |
0 |
0 |
0 |
20 - 5 = 15 |
15 |
10 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 40, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x34 = min(40,15) = 15.
5 |
3 |
4 |
x |
x |
x |
0 |
x |
x |
10 |
5 |
x |
x |
0 |
x |
x |
x |
3 |
4 |
0 |
40 - 15 = 25 |
0 |
0 |
0 |
15 - 15 = 0 |
15 |
10 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 25, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x35 = min(25,15) = 15.
5 |
3 |
4 |
x |
x |
x |
0 |
x |
x |
10 |
5 |
x |
x |
0 |
x |
x |
x |
3 |
4 |
0 |
25 - 15 = 10 |
0 |
0 |
0 |
0 |
15 - 15 = 0 |
10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x36 = min(10,10) = 10.
5 |
3 |
4 |
x |
x |
x |
0 |
x |
x |
10 |
5 |
x |
x |
0 |
x |
x |
x |
3 |
4 |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5[25] |
3[10] |
4[5] |
6 |
4 |
0 |
40 |
2 |
3 |
4 |
10[15] |
5[5] |
7 |
0 |
20 |
3 |
4 |
6 |
9 |
3[15] |
4[15] |
0[10] |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 3*10 + 4*5 + 10*15 + 5*5 + 3*15 + 4*15 + 0*10 = 455
Этап II. Улучшение опорного плана.
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v1 = 5; 0 + v1 = 5; v1 = 5
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
u2 + v3 = 10; 4 + u2 = 10; u2 = 6
u2 + v4 = 5; 6 + v4 = 5; v4 = -1
u3 + v4 = 3; -1 + u3 = 3; u3 = 4
u3 + v5 = 4; 4 + v5 = 4; v5 = 0
u3 + v6 = 0; 4 + v6 = 0; v6 = -4
|
v1=5 |
v2=3 |
v3=4 |
v4=-1 |
v5=0 |
v6=-4 |
u1=0 |
5[25] |
3[10] |
4[5] |
6 |
4 |
0 |
u2=6 |
3 |
4 |
10[15] |
5[5] |
7 |
0 |
u3=4 |
4 |
6 |
9 |
3[15] |
4[15] |
0[10] |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij
(2;1): 6 + 5 > 3; ∆21 = 6 + 5 - 3 = 8
(2;2): 6 + 3 > 4; ∆22 = 6 + 3 - 4 = 5
(2;6): 6 + -4 > 0; ∆26 = 6 + -4 - 0 = 2
(3;1): 4 + 5 > 4; ∆31 = 4 + 5 - 4 = 5
(3;2): 4 + 3 > 6; ∆32 = 4 + 3 - 6 = 1
max(8,5,2,5,1) = 8
Выбираем максимальную оценку свободной клетки (2;1): 3
Для этого в перспективную клетку (2;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5[25][-] |
3[10] |
4[5][+] |
6 |
4 |
0 |
40 |
2 |
3[+] |
4 |
10[15][-] |
5[5] |
7 |
0 |
20 |
3 |
4 |
6 |
9 |
3[15] |
4[15] |
0[10] |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
Цикл приведен в таблице (2,1; 2,3; 1,3; 1,1; ).
Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 15. Прибавляем 15 к объемам грузов, стоящих в плюсовых клетках и вычитаем 15 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5[10] |
3[10] |
4[20] |
6 |
4 |
0 |
40 |
2 |
3[15] |
4 |
10 |
5[5] |
7 |
0 |
20 |
3 |
4 |
6 |
9 |
3[15] |
4[15] |
0[10] |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v1 = 5; 0 + v1 = 5; v1 = 5
u2 + v1 = 3; 5 + u2 = 3; u2 = -2
u2 + v4 = 5; -2 + v4 = 5; v4 = 7
u3 + v4 = 3; 7 + u3 = 3; u3 = -4
u3 + v5 = 4; -4 + v5 = 4; v5 = 8
u3 + v6 = 0; -4 + v6 = 0; v6 = 4
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
|
v1=5 |
v2=3 |
v3=4 |
v4=7 |
v5=8 |
v6=4 |
u1=0 |
5[10] |
3[10] |
4[20] |
6 |
4 |
0 |
u2=-2 |
3[15] |
4 |
10 |
5[5] |
7 |
0 |
u3=-4 |
4 |
6 |
9 |
3[15] |
4[15] |
0[10] |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij
(1;4): 0 + 7 > 6; ∆14 = 0 + 7 - 6 = 1
(1;5): 0 + 8 > 4; ∆15 = 0 + 8 - 4 = 4
(1;6): 0 + 4 > 0; ∆16 = 0 + 4 - 0 = 4
(2;6): -2 + 4 > 0; ∆26 = -2 + 4 - 0 = 2
max(1,4,4,2) = 4
Выбираем максимальную оценку свободной клетки (1;5): 4
Для этого в перспективную клетку (1;5) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5[10][-] |
3[10] |
4[20] |
6 |
4[+] |
0 |
40 |
2 |
3[15][+] |
4 |
10 |
5[5][-] |
7 |
0 |
20 |
3 |
4 |
6 |
9 |
3[15][+] |
4[15][-] |
0[10] |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
Цикл приведен в таблице (1,5; 1,1; 2,1; 2,4; 3,4; 3,5; ).
Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 4) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5[5] |
3[10] |
4[20] |
6 |
4[5] |
0 |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
0 |
20 |
3 |
4 |
6 |
9 |
3[20] |
4[10] |
0[10] |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v1 = 5; 0 + v1 = 5; v1 = 5
u2 + v1 = 3; 5 + u2 = 3; u2 = -2
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
u1 + v5 = 4; 0 + v5 = 4; v5 = 4
u3 + v5 = 4; 4 + u3 = 4; u3 = 0
u3 + v4 = 3; 0 + v4 = 3; v4 = 3
u3 + v6 = 0; 0 + v6 = 0; v6 = 0
|
v1=5 |
v2=3 |
v3=4 |
v4=3 |
v5=4 |
v6=0 |
u1=0 |
5[5] |
3[10] |
4[20] |
6 |
4[5] |
0 |
u2=-2 |
3[20] |
4 |
10 |
5 |
7 |
0 |
u3=0 |
4 |
6 |
9 |
3[20] |
4[10] |
0[10] |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij
(3;1): 0 + 5 > 4; ∆31 = 0 + 5 - 4 = 1
Выбираем максимальную оценку свободной клетки (3;1): 4
Для этого в перспективную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5[5][-] |
3[10] |
4[20] |
6 |
4[5][+] |
0 |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
0 |
20 |
3 |
4[+] |
6 |
9 |
3[20] |
4[10][-] |
0[10] |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
Цикл приведен в таблице (3,1; 3,5; 1,5; 1,1; ).
Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 1) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
|
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
1 |
5 |
3[10] |
4[20] |
6 |
4[10] |
0 |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
0 |
20 |
3 |
4[5] |
6 |
9 |
3[20] |
4[5] |
0[10] |
40 |
Потребности |
25 |
10 |
20 |
20 |
15 |
10 |
|
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
u1 + v5 = 4; 0 + v5 = 4; v5 = 4
u3 + v5 = 4; 4 + u3 = 4; u3 = 0
u3 + v1 = 4; 0 + v1 = 4; v1 = 4
u2 + v1 = 3; 4 + u2 = 3; u2 = -1
u3 + v4 = 3; 0 + v4 = 3; v4 = 3
u3 + v6 = 0; 0 + v6 = 0; v6 = 0
|
v1=4 |
v2=3 |
v3=4 |
v4=3 |
v5=4 |
v6=0 |
u1=0 |
5 |
3[10] |
4[20] |
6 |
4[10] |
0 |
u2=-1 |
3[20] |
4 |
10 |
5 |
7 |
0 |
u3=0 |
4[5] |
6 |
9 |
3[20] |
4[5] |
0[10] |
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj ≤ cij.
Минимальные затраты составят:
F(x) = 3*10 + 4*20 + 4*10 + 3*20 + 4*5 + 3*20 + 4*5 + 0*10 = 310
Анализ оптимального плана.
Из 1-го склада необходимо груз направить в 2-й магазин (10), в 3-й магазин (20), в 5-й магазин (10)
Из 2-го склада необходимо весь груз направить в 1-й магазин
Из 3-го склада необходимо груз направить в 1-й магазин (5), в 4-й магазин (20), в 5-й магазин (5)
На 3-ом складе остался невостребованным груз в количестве 10 ед.
Оптимальный план является вырожденным, так как базисная переменная x36=0.
б)
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5 |
3 |
4 |
6 |
4 |
40 |
2 |
3 |
4 |
10 |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
|
4 |
5 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Поскольку в матрице присутствуют запрещенные к размещению клетки, то для отыскания оптимального плана достаточно заменить их на максимальные тарифы (10 умноженное на 3).
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5 |
3 |
4 |
6 |
4 |
40 |
2 |
3 |
4 |
10 |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4 |
5 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Проверим необходимое и достаточное условие разрешимости задачи.
∑a = 40 + 20 + 5 = 65
∑b = 25 + 10 + 20 + 5 + 15 = 75
Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равной 10 (75—65). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.
Занесем исходные данные в распределительную таблицу.
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5 |
3 |
4 |
6 |
4 |
40 |
2 |
3 |
4 |
10 |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4 |
5 |
4 |
0 |
0 |
0 |
0 |
0 |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Этап I. Поиск первого опорного плана.
1. Используя метод северо-западного угла, построим первый опорный план транспортной задачи.
План начинается заполняться с верхнего левого угла.
Искомый элемент равен 5
Для этого элемента запасы равны 40, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(40,25) = 25.
5 |
3 |
4 |
6 |
4 |
40 - 25 = 15 |
x |
4 |
10 |
5 |
7 |
20 |
x |
6 |
9 |
30 |
4 |
5 |
x |
0 |
0 |
0 |
0 |
10 |
25 - 25 = 0 |
10 |
20 |
5 |
15 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 15, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x12 = min(15,10) = 10.
5 |
3 |
4 |
6 |
4 |
15 - 10 = 5 |
x |
x |
10 |
5 |
7 |
20 |
x |
x |
9 |
30 |
4 |
5 |
x |
x |
0 |
0 |
0 |
10 |
0 |
10 - 10 = 0 |
20 |
5 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 20. Поскольку минимальным является 5, то вычитаем его.
x13 = min(5,20) = 5.
5 |
3 |
4 |
x |
x |
5 - 5 = 0 |
x |
x |
10 |
5 |
7 |
20 |
x |
x |
9 |
30 |
4 |
5 |
x |
x |
0 |
0 |
0 |
10 |
0 |
0 |
20 - 5 = 15 |
5 |
15 |
0 |
Искомый элемент равен 10
Для этого элемента запасы равны 20, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x23 = min(20,15) = 15.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
7 |
20 - 15 = 5 |
x |
x |
x |
30 |
4 |
5 |
x |
x |
x |
0 |
0 |
10 |
0 |
0 |
15 - 15 = 0 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x24 = min(5,5) = 5.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
5 - 5 = 0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3[10] |
4[5] |
6 |
4 |
40 |
2 |
3 |
4 |
10[15] |
5[5] |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 3*10 + 4*5 + 10*15 + 5*5 + 4*5 + 0*10 = 370
Искомый элемент равен 3
Для этого элемента запасы равны 40, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x12 = min(40,10) = 10.
5 |
3 |
4 |
6 |
4 |
40 - 10 = 30 |
3 |
x |
10 |
5 |
7 |
20 |
4 |
x |
9 |
30 |
4 |
5 |
0 |
x |
0 |
0 |
0 |
10 |
25 |
10 - 10 = 0 |
20 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 30, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(30,25) = 25.
5 |
3 |
4 |
6 |
4 |
30 - 25 = 5 |
x |
x |
10 |
5 |
7 |
20 |
x |
x |
9 |
30 |
4 |
5 |
x |
x |
0 |
0 |
0 |
10 |
25 - 25 = 0 |
0 |
20 |
5 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 20. Поскольку минимальным является 5, то вычитаем его.
x13 = min(5,20) = 5.
5 |
3 |
4 |
x |
x |
5 - 5 = 0 |
x |
x |
10 |
5 |
7 |
20 |
x |
x |
9 |
30 |
4 |
5 |
x |
x |
0 |
0 |
0 |
10 |
0 |
0 |
20 - 5 = 15 |
5 |
15 |
0 |
Искомый элемент равен 10
Для этого элемента запасы равны 20, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x23 = min(20,15) = 15.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
7 |
20 - 15 = 5 |
x |
x |
x |
30 |
4 |
5 |
x |
x |
x |
0 |
0 |
10 |
0 |
0 |
15 - 15 = 0 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x24 = min(5,5) = 5.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
5 - 5 = 0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3[10] |
4[5] |
6 |
4 |
40 |
2 |
3 |
4 |
10[15] |
5[5] |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 3*10 + 4*5 + 10*15 + 5*5 + 4*5 + 0*10 = 370
Искомый элемент равен 4
Для этого элемента запасы равны 40, потребности 20. Поскольку минимальным является 20, то вычитаем его.
x13 = min(40,20) = 20.
5 |
3 |
4 |
6 |
4 |
40 - 20 = 20 |
3 |
4 |
x |
5 |
7 |
20 |
4 |
6 |
x |
30 |
4 |
5 |
0 |
0 |
x |
0 |
0 |
10 |
25 |
10 |
20 - 20 = 0 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 20, потребности 25. Поскольку минимальным является 20, то вычитаем его.
x11 = min(20,25) = 20.
5 |
x |
4 |
x |
x |
20 - 20 = 0 |
3 |
4 |
x |
5 |
7 |
20 |
4 |
6 |
x |
30 |
4 |
5 |
0 |
0 |
x |
0 |
0 |
10 |
25 - 20 = 5 |
10 |
0 |
5 |
15 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 20, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x21 = min(20,5) = 5.
5 |
x |
4 |
x |
x |
0 |
3 |
4 |
x |
5 |
7 |
20 - 5 = 15 |
x |
6 |
x |
30 |
4 |
5 |
x |
0 |
x |
0 |
0 |
10 |
5 - 5 = 0 |
10 |
0 |
5 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 15, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x22 = min(15,10) = 10.
5 |
x |
4 |
x |
x |
0 |
3 |
4 |
x |
5 |
7 |
15 - 10 = 5 |
x |
x |
x |
30 |
4 |
5 |
x |
x |
x |
0 |
0 |
10 |
0 |
10 - 10 = 0 |
0 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x24 = min(5,5) = 5.
5 |
x |
4 |
x |
x |
0 |
3 |
4 |
x |
5 |
x |
5 - 5 = 0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
x |
4 |
x |
x |
0 |
3 |
4 |
x |
5 |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
x |
4 |
x |
x |
0 |
3 |
4 |
x |
5 |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[20] |
3 |
4[20] |
6 |
4 |
40 |
2 |
3[5] |
4[10] |
10 |
5[5] |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*20 + 4*20 + 3*5 + 4*10 + 5*5 + 4*5 + 0*10 = 280
Искомый элемент равен 6
Для этого элемента запасы равны 40, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x14 = min(40,5) = 5.
5 |
3 |
4 |
6 |
4 |
40 - 5 = 35 |
3 |
4 |
10 |
x |
7 |
20 |
4 |
6 |
9 |
x |
4 |
5 |
0 |
0 |
0 |
x |
0 |
10 |
25 |
10 |
20 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 35, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(35,25) = 25.
5 |
3 |
4 |
6 |
4 |
35 - 25 = 10 |
x |
4 |
10 |
x |
7 |
20 |
x |
6 |
9 |
x |
4 |
5 |
x |
0 |
0 |
x |
0 |
10 |
25 - 25 = 0 |
10 |
20 |
0 |
15 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x12 = min(10,10) = 10.
5 |
3 |
x |
6 |
x |
10 - 10 = 0 |
x |
x |
10 |
x |
7 |
20 |
x |
x |
9 |
x |
4 |
5 |
x |
x |
0 |
x |
0 |
10 |
0 |
10 - 10 = 0 |
20 |
0 |
15 |
0 |
Искомый элемент равен 10
Для этого элемента запасы равны 20, потребности 20. Поскольку минимальным является 20, то вычитаем его.
x23 = min(20,20) = 20.
5 |
3 |
x |
6 |
x |
0 |
x |
x |
10 |
x |
x |
20 - 20 = 0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
20 - 20 = 0 |
0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
3 |
x |
6 |
x |
0 |
x |
x |
10 |
x |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
3 |
x |
6 |
x |
0 |
x |
x |
10 |
x |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3[10] |
4 |
6[5] |
4 |
40 |
2 |
3 |
4 |
10[20] |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 3*10 + 6*5 + 10*20 + 4*5 + 0*10 = 405
Искомый элемент равен 4
Для этого элемента запасы равны 40, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x15 = min(40,15) = 15.
5 |
3 |
4 |
6 |
4 |
40 - 15 = 25 |
3 |
4 |
10 |
5 |
x |
20 |
4 |
6 |
9 |
30 |
x |
5 |
0 |
0 |
0 |
0 |
x |
10 |
25 |
10 |
20 |
5 |
15 - 15 = 0 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 25, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(25,25) = 25.
5 |
x |
x |
x |
4 |
25 - 25 = 0 |
x |
4 |
10 |
5 |
x |
20 |
x |
6 |
9 |
30 |
x |
5 |
x |
0 |
0 |
0 |
x |
10 |
25 - 25 = 0 |
10 |
20 |
5 |
0 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 20, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x22 = min(20,10) = 10.
5 |
x |
x |
x |
4 |
0 |
x |
4 |
10 |
5 |
x |
20 - 10 = 10 |
x |
x |
9 |
30 |
x |
5 |
x |
x |
0 |
0 |
x |
10 |
0 |
10 - 10 = 0 |
20 |
5 |
0 |
0 |
Искомый элемент равен 10
Для этого элемента запасы равны 10, потребности 20. Поскольку минимальным является 10, то вычитаем его.
x23 = min(10,20) = 10.
5 |
x |
x |
x |
4 |
0 |
x |
4 |
10 |
x |
x |
10 - 10 = 0 |
x |
x |
9 |
30 |
x |
5 |
x |
x |
0 |
0 |
x |
10 |
0 |
0 |
20 - 10 = 10 |
5 |
0 |
0 |
Искомый элемент равен 9
Для этого элемента запасы равны 5, потребности 10. Поскольку минимальным является 5, то вычитаем его.
x33 = min(5,10) = 5.
5 |
x |
x |
x |
4 |
0 |
x |
4 |
10 |
x |
x |
0 |
x |
x |
9 |
x |
x |
5 - 5 = 0 |
x |
x |
0 |
0 |
x |
10 |
0 |
0 |
10 - 5 = 5 |
5 |
0 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x43 = min(10,5) = 5.
5 |
x |
x |
x |
4 |
0 |
x |
4 |
10 |
x |
x |
0 |
x |
x |
9 |
x |
x |
0 |
x |
x |
0 |
0 |
x |
10 - 5 = 5 |
0 |
0 |
5 - 5 = 0 |
5 |
0 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x44 = min(5,5) = 5.
5 |
x |
x |
x |
4 |
0 |
x |
4 |
10 |
x |
x |
0 |
x |
x |
9 |
x |
x |
0 |
x |
x |
0 |
0 |
x |
5 - 5 = 0 |
0 |
0 |
0 |
5 - 5 = 0 |
0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3 |
4 |
6 |
4[15] |
40 |
2 |
3 |
4[10] |
10[10] |
5 |
7 |
20 |
3 |
4 |
6 |
9[5] |
30 |
4 |
5 |
4 |
0 |
0 |
0[5] |
0[5] |
0 |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 4*15 + 4*10 + 10*10 + 9*5 + 0*5 + 0*5 = 370
Искомый элемент равен 3
Для этого элемента запасы равны 20, потребности 25. Поскольку минимальным является 20, то вычитаем его.
x21 = min(20,25) = 20.
5 |
3 |
4 |
6 |
4 |
40 |
3 |
x |
x |
x |
x |
20 - 20 = 0 |
4 |
6 |
9 |
30 |
4 |
5 |
0 |
0 |
0 |
0 |
0 |
10 |
25 - 20 = 5 |
10 |
20 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 40, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x11 = min(40,5) = 5.
5 |
3 |
4 |
6 |
4 |
40 - 5 = 35 |
3 |
x |
x |
x |
x |
0 |
x |
6 |
9 |
30 |
4 |
5 |
x |
0 |
0 |
0 |
0 |
10 |
5 - 5 = 0 |
10 |
20 |
5 |
15 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 35, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x12 = min(35,10) = 10.
5 |
3 |
4 |
6 |
4 |
35 - 10 = 25 |
3 |
x |
x |
x |
x |
0 |
x |
x |
9 |
30 |
4 |
5 |
x |
x |
0 |
0 |
0 |
10 |
0 |
10 - 10 = 0 |
20 |
5 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 25, потребности 20. Поскольку минимальным является 20, то вычитаем его.
x13 = min(25,20) = 20.
5 |
3 |
4 |
6 |
4 |
25 - 20 = 5 |
3 |
x |
x |
x |
x |
0 |
x |
x |
x |
30 |
4 |
5 |
x |
x |
x |
0 |
0 |
10 |
0 |
0 |
20 - 20 = 0 |
5 |
15 |
0 |
Искомый элемент равен 6
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x14 = min(5,5) = 5.
5 |
3 |
4 |
6 |
x |
5 - 5 = 0 |
3 |
x |
x |
x |
x |
0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
3 |
4 |
6 |
x |
0 |
3 |
x |
x |
x |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
3 |
4 |
6 |
x |
0 |
3 |
x |
x |
x |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[5] |
3[10] |
4[20] |
6[5] |
4 |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*5 + 3*10 + 4*20 + 6*5 + 3*20 + 4*5 + 0*10 = 245
Искомый элемент равен 4
Для этого элемента запасы равны 20, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x22 = min(20,10) = 10.
5 |
x |
4 |
6 |
4 |
40 |
3 |
4 |
10 |
5 |
7 |
20 - 10 = 10 |
4 |
x |
9 |
30 |
4 |
5 |
0 |
x |
0 |
0 |
0 |
10 |
25 |
10 - 10 = 0 |
20 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 40, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(40,25) = 25.
5 |
x |
4 |
6 |
4 |
40 - 25 = 15 |
x |
4 |
10 |
5 |
7 |
10 |
x |
x |
9 |
30 |
4 |
5 |
x |
x |
0 |
0 |
0 |
10 |
25 - 25 = 0 |
0 |
20 |
5 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 15, потребности 20. Поскольку минимальным является 15, то вычитаем его.
x13 = min(15,20) = 15.
5 |
x |
4 |
x |
x |
15 - 15 = 0 |
x |
4 |
10 |
5 |
7 |
10 |
x |
x |
9 |
30 |
4 |
5 |
x |
x |
0 |
0 |
0 |
10 |
0 |
0 |
20 - 15 = 5 |
5 |
15 |
0 |
Искомый элемент равен 10
Для этого элемента запасы равны 10, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x23 = min(10,5) = 5.
5 |
x |
4 |
x |
x |
0 |
x |
4 |
10 |
5 |
7 |
10 - 5 = 5 |
x |
x |
x |
30 |
4 |
5 |
x |
x |
x |
0 |
0 |
10 |
0 |
0 |
5 - 5 = 0 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x24 = min(5,5) = 5.
5 |
x |
4 |
x |
x |
0 |
x |
4 |
10 |
5 |
x |
5 - 5 = 0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
x |
4 |
x |
x |
0 |
x |
4 |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
x |
4 |
x |
x |
0 |
x |
4 |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3 |
4[15] |
6 |
4 |
40 |
2 |
3 |
4[10] |
10[5] |
5[5] |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 4*15 + 4*10 + 10*5 + 5*5 + 4*5 + 0*10 = 320
Искомый элемент равен 10
Для этого элемента запасы равны 20, потребности 20. Поскольку минимальным является 20, то вычитаем его.
x23 = min(20,20) = 20.
5 |
3 |
x |
6 |
4 |
40 |
x |
x |
10 |
x |
x |
20 - 20 = 0 |
4 |
6 |
x |
30 |
4 |
5 |
0 |
0 |
x |
0 |
0 |
10 |
25 |
10 |
20 - 20 = 0 |
5 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 40, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(40,25) = 25.
5 |
3 |
x |
6 |
4 |
40 - 25 = 15 |
x |
x |
10 |
x |
x |
0 |
x |
6 |
x |
30 |
4 |
5 |
x |
0 |
x |
0 |
0 |
10 |
25 - 25 = 0 |
10 |
0 |
5 |
15 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 15, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x12 = min(15,10) = 10.
5 |
3 |
x |
6 |
4 |
15 - 10 = 5 |
x |
x |
10 |
x |
x |
0 |
x |
x |
x |
30 |
4 |
5 |
x |
x |
x |
0 |
0 |
10 |
0 |
10 - 10 = 0 |
0 |
5 |
15 |
0 |
Искомый элемент равен 6
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x14 = min(5,5) = 5.
5 |
3 |
x |
6 |
x |
5 - 5 = 0 |
x |
x |
10 |
x |
x |
0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
3 |
x |
6 |
x |
0 |
x |
x |
10 |
x |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
3 |
x |
6 |
x |
0 |
x |
x |
10 |
x |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3[10] |
4 |
6[5] |
4 |
40 |
2 |
3 |
4 |
10[20] |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 3*10 + 6*5 + 10*20 + 4*5 + 0*10 = 405
Искомый элемент равен 5
Для этого элемента запасы равны 20, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x24 = min(20,5) = 5.
5 |
3 |
4 |
x |
4 |
40 |
3 |
4 |
10 |
5 |
7 |
20 - 5 = 15 |
4 |
6 |
9 |
x |
4 |
5 |
0 |
0 |
0 |
x |
0 |
10 |
25 |
10 |
20 |
5 - 5 = 0 |
15 |
0 |
Искомый элемент равен 5
Для этого элемента запасы равны 40, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x11 = min(40,25) = 25.
5 |
3 |
4 |
x |
4 |
40 - 25 = 15 |
x |
4 |
10 |
5 |
7 |
15 |
x |
6 |
9 |
x |
4 |
5 |
x |
0 |
0 |
x |
0 |
10 |
25 - 25 = 0 |
10 |
20 |
0 |
15 |
0 |
Искомый элемент равен 3
Для этого элемента запасы равны 15, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x12 = min(15,10) = 10.
5 |
3 |
4 |
x |
4 |
15 - 10 = 5 |
x |
x |
10 |
5 |
7 |
15 |
x |
x |
9 |
x |
4 |
5 |
x |
x |
0 |
x |
0 |
10 |
0 |
10 - 10 = 0 |
20 |
0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 20. Поскольку минимальным является 5, то вычитаем его.
x13 = min(5,20) = 5.
5 |
3 |
4 |
x |
x |
5 - 5 = 0 |
x |
x |
10 |
5 |
7 |
15 |
x |
x |
9 |
x |
4 |
5 |
x |
x |
0 |
x |
0 |
10 |
0 |
0 |
20 - 5 = 15 |
0 |
15 |
0 |
Искомый элемент равен 10
Для этого элемента запасы равны 15, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x23 = min(15,15) = 15.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
15 - 15 = 0 |
x |
x |
x |
x |
4 |
5 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
15 - 15 = 0 |
0 |
15 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 5, потребности 15. Поскольку минимальным является 5, то вычитаем его.
x35 = min(5,15) = 5.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
5 - 5 = 0 |
x |
x |
x |
x |
0 |
10 |
0 |
0 |
0 |
0 |
15 - 5 = 10 |
0 |
Искомый элемент равен 0
Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x45 = min(10,10) = 10.
5 |
3 |
4 |
x |
x |
0 |
x |
x |
10 |
5 |
x |
0 |
x |
x |
x |
x |
4 |
0 |
x |
x |
x |
x |
0 |
10 - 10 = 0 |
0 |
0 |
0 |
0 |
10 - 10 = 0 |
0 |
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3[10] |
4[5] |
6 |
4 |
40 |
2 |
3 |
4 |
10[15] |
5[5] |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Строим новый план.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 3*10 + 4*5 + 10*15 + 5*5 + 4*5 + 0*10 = 370
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[25] |
3[10] |
4[5] |
6 |
4 |
40 |
2 |
3 |
4 |
10[15] |
5[5] |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0 |
0[10] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 8. Следовательно, опорный план является вырожденным.
Значение целевой функции для этого опорного плана равно:
F(x) = 5*25 + 3*10 + 4*5 + 10*15 + 5*5 + 4*5 + 0*10 = 370
На протяжении многих итераций так и не удалось получить невырожденный план.
Для получения невырожденного плана принудительно добавляем нуль [0] в клетку (1;5);
Этап II. Улучшение опорного плана.
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v1 = 5; 0 + v1 = 5; v1 = 5
u2 + v1 = 3; 5 + u2 = 3; u2 = -2
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
u1 + v4 = 6; 0 + v4 = 6; v4 = 6
u1 + v5 = 4; 0 + v5 = 4; v5 = 4
u3 + v5 = 4; 4 + u3 = 4; u3 = 0
u4 + v5 = 0; 4 + u4 = 0; u4 = -4
|
v1=5 |
v2=3 |
v3=4 |
v4=6 |
v5=4 |
u1=0 |
5[5] |
3[10] |
4[20] |
6[5] |
4[0] |
u2=-2 |
3[20] |
4 |
10 |
5 |
7 |
u3=0 |
4 |
6 |
9 |
30 |
4[5] |
u4=-4 |
0 |
0 |
0 |
0 |
0[10] |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij
(3;1): 0 + 5 > 4; ∆31 = 0 + 5 - 4 = 1
(4;1): -4 + 5 > 0; ∆41 = -4 + 5 - 0 = 1
(4;4): -4 + 6 > 0; ∆44 = -4 + 6 - 0 = 2
max(1,1,2) = 2
Выбираем максимальную оценку свободной клетки (4;4): 0
Для этого в перспективную клетку (4;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[5] |
3[10] |
4[20] |
6[5][-] |
4[0][+] |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0[+] |
0[10][-] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Цикл приведен в таблице (4,4; 4,5; 1,5; 1,4; ).
Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 4) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[5] |
3[10] |
4[20] |
6 |
4[5] |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
20 |
3 |
4 |
6 |
9 |
30 |
4[5] |
5 |
4 |
0 |
0 |
0 |
0[5] |
0[5] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v1 = 5; 0 + v1 = 5; v1 = 5
u2 + v1 = 3; 5 + u2 = 3; u2 = -2
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
u1 + v5 = 4; 0 + v5 = 4; v5 = 4
u3 + v5 = 4; 4 + u3 = 4; u3 = 0
u4 + v5 = 0; 4 + u4 = 0; u4 = -4
u4 + v4 = 0; -4 + v4 = 0; v4 = 4
|
v1=5 |
v2=3 |
v3=4 |
v4=4 |
v5=4 |
u1=0 |
5[5] |
3[10] |
4[20] |
6 |
4[5] |
u2=-2 |
3[20] |
4 |
10 |
5 |
7 |
u3=0 |
4 |
6 |
9 |
30 |
4[5] |
u4=-4 |
0 |
0 |
0 |
0[5] |
0[5] |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij
(3;1): 0 + 5 > 4; ∆31 = 0 + 5 - 4 = 1
(4;1): -4 + 5 > 0; ∆41 = -4 + 5 - 0 = 1
max(1,1) = 1
Выбираем максимальную оценку свободной клетки (3;1): 4
Для этого в перспективную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[5][-] |
3[10] |
4[20] |
6 |
4[5][+] |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
20 |
3 |
4[+] |
6 |
9 |
30 |
4[5][-] |
5 |
4 |
0 |
0 |
0 |
0[5] |
0[5] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Цикл приведен в таблице (3,1; 3,5; 1,5; 1,1; ).
Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 5) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[0] |
3[10] |
4[20] |
6 |
4[10] |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
20 |
3 |
4[5] |
6 |
9 |
30 |
4 |
5 |
4 |
0 |
0 |
0 |
0[5] |
0[5] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v1 = 5; 0 + v1 = 5; v1 = 5
u2 + v1 = 3; 5 + u2 = 3; u2 = -2
u3 + v1 = 4; 5 + u3 = 4; u3 = -1
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
u1 + v5 = 4; 0 + v5 = 4; v5 = 4
u4 + v5 = 0; 4 + u4 = 0; u4 = -4
u4 + v4 = 0; -4 + v4 = 0; v4 = 4
|
v1=5 |
v2=3 |
v3=4 |
v4=4 |
v5=4 |
u1=0 |
5[0] |
3[10] |
4[20] |
6 |
4[10] |
u2=-2 |
3[20] |
4 |
10 |
5 |
7 |
u3=-1 |
4[5] |
6 |
9 |
30 |
4 |
u4=-4 |
0 |
0 |
0 |
0[5] |
0[5] |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij
(4;1): -4 + 5 > 0; ∆41 = -4 + 5 - 0 = 1
Выбираем максимальную оценку свободной клетки (4;1): 0
Для этого в перспективную клетку (4;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5[0][-] |
3[10] |
4[20] |
6 |
4[10][+] |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
20 |
3 |
4[5] |
6 |
9 |
30 |
4 |
5 |
4 |
0[+] |
0 |
0 |
0[5] |
0[5][-] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Цикл приведен в таблице (4,1; 4,5; 1,5; 1,1; ).
Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 1) = 0. Прибавляем 0 к объемам грузов, стоящих в плюсовых клетках и вычитаем 0 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
|
1 |
2 |
3 |
4 |
5 |
Запасы |
1 |
5 |
3[10] |
4[20] |
6 |
4[10] |
40 |
2 |
3[20] |
4 |
10 |
5 |
7 |
20 |
3 |
4[5] |
6 |
9 |
30 |
4 |
5 |
4 |
0[0] |
0 |
0 |
0[5] |
0[5] |
10 |
Потребности |
25 |
10 |
20 |
5 |
15 |
|
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v2 = 3; 0 + v2 = 3; v2 = 3
u1 + v3 = 4; 0 + v3 = 4; v3 = 4
u1 + v5 = 4; 0 + v5 = 4; v5 = 4
u4 + v5 = 0; 4 + u4 = 0; u4 = -4
u4 + v1 = 0; -4 + v1 = 0; v1 = 4
u2 + v1 = 3; 4 + u2 = 3; u2 = -1
u3 + v1 = 4; 4 + u3 = 4; u3 = 0
u4 + v4 = 0; -4 + v4 = 0; v4 = 4
|
v1=4 |
v2=3 |
v3=4 |
v4=4 |
v5=4 |
u1=0 |
5 |
3[10] |
4[20] |
6 |
4[10] |
u2=-1 |
3[20] |
4 |
10 |
5 |
7 |
u3=0 |
4[5] |
6 |
9 |
30 |
4 |
u4=-4 |
0[0] |
0 |
0 |
0[5] |
0[5] |
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj ≤ cij.
Минимальные затраты составят:
F(x) = 3*10 + 4*20 + 4*10 + 3*20 + 4*5 + 0*5 + 0*5 = 230
Анализ оптимального плана.
Из 1-го склада необходимо груз направить в 2-й магазин (10), в 3-й магазин (20), в 5-й магазин (10)
Из 2-го склада необходимо весь груз направить в 1-й магазин
Из 3-го склада необходимо весь груз направить в 1-й магазин
Потребность 4-го магазина остается неудовлетворенной на 5 ед.
Оптимальный план является вырожденным, так как базисная переменная x44=0.
Потребность 5-го магазина остается неудовлетворенной на 5 ед.
Оптимальный план является вырожденным, так как базисная переменная x45=0.
Задача имеет множество оптимальных планов, поскольку оценка для (4;1) равна 0.
Таким образом, видим, что произойдет уменьшение значения целевой функции на: 310-230=80 д.е.
