Задание № 3

На основе данных провести идентификацию модели и описать процедуру оценивания параметров уравнений структурной формы модели.

	y2	y3	x1	x2	x3
y11	0	0	a11	a21	a31
	y1	y3	x1	x2	x3
y23	0	b32	a12	a22	a32
	y1	y2	x1	x2	x3
y31	b13	b23	a13	0	0

Решение:

Система уравнений, соответствующая варианту, примет вид:

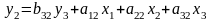
В этой системе y₁, y₂,y₃ - эндогенные переменные (K=3);

x₁, x₂, x₃ - предопределенные переменные (M=3).

K-1=2; K+M=6.

Составим приведенную форму модели:

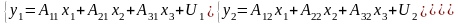
Проверим, как выполняется необходимое условие идентификации для каждого уравнения.

Для 1-ого уравнения имеем: k₁=1; m₁=3;

M-m₁=0 = k₁-1=0, следовательно, 1-ое уравнение точно идентифицированно.

Для 2-ого уравнения имеем: k₂=2; m₂=3;

M-m₂=0 < k₂-1=1, следовательно, 2-ое уравнение неидентифицированно.

Для 3-его уравнения имеем: k₃=3; m₃=1;

M-m₃=2 =k₃-1=2, следовательно, 3-е уравнение точно идентифицированно.

Рассмотрим, как выполняется достаточное условие идентификации для каждого уравнения системы. Для того, чтобы оно выполнялось, необходимо, чтобы определитель матрицы А (матрицы коэффициентов при переменных, не входящих в это уравнение) был равен К-1=2.

Составим матрицу А для 1-ого уравнения системы. В 1-ом уравнении отсутствуют переменная y₂, y₃. Поэтому матрица А будет иметь вид:

y2	y3
1	b32	во 2-ом уравнении
b23	1	в 3-ем уравнении

Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 1-ое уравнение модели точно идентифицированно.

Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствует переменная y ₁.

Матрица А будет иметь вид:

y1
1	во 1-ом уравнении
b13	в 3-ем уравнении

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 2-ое уравнение модели неидентифицированно.

Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные x₂, x₃. Поэтому матрица А будет иметь вид:

x2	x3
a21	a31	во 1-ом уравнении
a22	a32	во 2-ом уравнении

Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 3-е уравнение модели точно идентифицированно.

Сделаем выводы: 2-ое уравнение системы неидентифицированно, 1-е и 3-е уравнения точно идентифицированны.

Следовательно, система в целом является неидентифицируемой.

Параметры уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.

Задание № 4

На основе данных, постройте модель временного ряда. Для этого требуется:

1. Построить коррелограмму и определить, имеет ли ряд тенденцию и сезонные колебания.

2. Провести сглаживание ряда скользящей средней и рассчитать значения сезонной составляющей.

3. Построить уравнения тренда и сделать выводы.

4. На основе полученной модели сделать прогноз на следующие два квартала с учетом выявленной сезонности.

Основные показатели развития производственной фирмы

за период с 2002 по 2007 гг. (по сопоставимой оценке)

N наблюдения	Год	Квартал	Объем производства продукции, млн. руб.
8	2003	4	1137
9	2004	1	1301
10		2	1038
11		3	780
12		4	1435
13	2005	1	1593
14		2	1658
15		3	1363
16		4	1737
17	2006	1	1719
18		2	1521
19		3	1049

Решение:

Чтобы построить коррелогорамму, исходный ряд динамики дополним рядами из уровней этого ряда, сдвинутыми во времени.

t	1	2	3	4	5	6	7	8	9	10	11	12
хt	-	1301	1038	780	1435	1593	1658	1363	1737	1719	1521	1049	rt,t-1=0,4195
xt-1	-	1137	1301	1038	780	1435	1593	1658	1363	1737	1719	1521
хt	-	-	1038	780	1435	1593	1658	1363	1737	1719	1521	1049	rt,t-2=0,0292
хt-2	-	-	1137	1301	1038	780	1435	1593	1658	1363	1737	1719
хt	-	-	-	780	1435	1593	1658	1363	1737	1719	1521	1049	rt,t-3=-0,0386
хt-3	-	-	-	1137	1301	1038	780	1435	1593	1658	1363	1737
хt	-	-	-	-	1435	1593	1658	1363	1737	1719	1521	1049	rt,t-4=0,2496
хt-4	-	-	-	-	1137	1301	1038	780	1435	1593	1658	1363
хt	-	-	-	-	-	1593	1658	1363	1737	1719	1521	1049	rt,t-5=-0,4880
хt-5	-	-	-	-	-	1137	1301	1038	780	1435	1593	1658

Рассчитаем коэффициенты корреляции:

1-ого порядка для рядов х_t и х_t-1,

2-ого порядка для рядов х_t и х_t-2,

3-его порядка для рядов х_t и х_t-3,

4-ого порядка для рядов х_t и х_t-4,

5-ого порядка для рядов х_t и х_t-5

Результаты расчетов представлены в следующей таблице.

Лаг (порядок) – L	rt,t-L	Коррелограмма
1	0,4195	****
2	0,0292	*
3	-0,0368	**
4	0,2496	***
5	-0,4880	*****

Вывод: в данном ряду динамики имеют место сезонные колебания.

Проведём сглаживание ряда скользящей средней и рассчитаем значения сезонной составляющей.

1. Произведем выравнивание ряда методом скользящей средней с периодом усреднения равным 3. Результаты представлены в таблице.

T	x	xc	x- xc
1	1137	-	-
2	1301	1158,67	142,33
3	1038	1039,67	-1,67
4	780	1084,33	-304,33
5	1435	1269,33	165,67
6	1593	1562	31
7	1658	1538	120
8	1363	1586	-223
9	1737	1606,33	130,67
10	1719	1659	60
11	1521	1429,67	91,33
12	1049	-	-

2) Расчет значений сезонной составляющей S_i, i=1;L, где L– число сезонов в году. L=4 (сезоны - кварталы).

Расчет значений сезонных составляющих осуществляется после устранения тенденции из исходных уровней ряда: x - x^c . Для дальнейшего расчета S_i построим отдельную таблицу. Строки данной таблицы соответствуют сезонам, столбцы - годам. В теле таблицы находятся значения: x - x^c. По этим данным рассчитываются средние оценки сезонных составляющих каждой строке (S^c_i). Если сумма всех средних оценок равна нулю (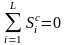 ), то данные средние и будут окончательными значениями сезонных составляющих (S_i=S^c_i). Если их сумма не равна нулю, то рассчитываются скорректированные значения сезонных составляющих вычитанием из средней оценки величины равной отношению суммы средних оценок к их общему числу ( ).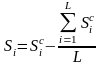

Номер сезона	Год 2004	Год 2005	Год 2006	Средняя оценка сезонной составляющей	Скорректированная оценка сезонной составляяющей Si
1	142,33	31	60	77,78	31,74
2	-1,67	120	91,33	69,88889	23,85
3	-304,33	-223	192,33	-111,667	-157,71
4	165,67	130,67		148,1667	102,13
Итого				184,17	0

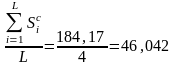
3) Устранение влияния сезонной составляющей из исходного ряда динамики:

x^S = x-S_i.

T	tу	x	xs	xstу	(tу)2
1	-11	1137	1105,26	-12157,9	121
2	-9	1301	1277,15	-11494,4	81
3	-7	1038	1195,71	-8369,96	49
4	-5	780	677,88	-3389,38	25
5	-3	1435	1403,26	-4209,79	9
6	-1	1593	1569,15	-1569,15	1
7	1	1658	1815,71	1815,708	1
8	3	1363	1260,88	3782,625	9
9	5	1737	1705,26	8526,319	25
10	7	1719	1695,15	11866,07	49
11	9	1521	1678,71	15108,38	81
12	11	1049	946,88	10415,63	121
Итого		16331	16331	10324,17	572