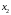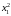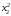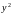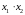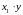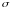Решение:
Выберем дополнительно еще один фактор – собственные оборотные средства.
Собственные
оборотные средства -
,
балансовая
прибыль -
,
дебиторская
задолженность -
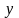 .
.
№ |
|
|
|
|
|
|
|
|
|
1 |
1243 |
122 |
26 |
1545049 |
14884 |
676 |
151646 |
32318 |
3172 |
2 |
1507 |
108 |
51 |
2271049 |
11664 |
2601 |
162756 |
76857 |
5508 |
3 |
947 |
108 |
41 |
896809 |
11664 |
1681 |
102276 |
38827 |
4428 |
4 |
1015 |
97 |
78 |
1030225 |
9409 |
6084 |
98455 |
79170 |
7566 |
5 |
1169 |
109 |
43 |
1366561 |
11881 |
1849 |
127421 |
50267 |
4687 |
6 |
1051 |
101 |
68 |
1104601 |
10201 |
4624 |
106151 |
71468 |
6868 |
7 |
1372 |
116 |
34 |
1882384 |
13456 |
1156 |
159152 |
46648 |
3944 |
8 |
1463 |
113 |
49 |
2140369 |
12769 |
2401 |
165319 |
71687 |
5537 |
9 |
684 |
112 |
40 |
467856 |
12544 |
1600 |
76608 |
27360 |
4480 |
10 |
1251 |
106 |
56 |
1565001 |
11236 |
3136 |
132606 |
70056 |
5936 |
11 |
1376 |
111 |
45 |
1893376 |
12321 |
2025 |
152736 |
61920 |
4995 |
12 |
1193 |
113 |
44 |
1423249 |
12769 |
1936 |
134809 |
52492 |
4972 |
13 |
1386 |
122 |
40 |
1920996 |
14884 |
1600 |
169092 |
55440 |
4880 |
14 |
1631 |
118 |
47 |
2660161 |
13924 |
2209 |
192458 |
76657 |
5546 |
15 |
1735 |
119 |
47 |
3010225 |
14161 |
2209 |
206465 |
81545 |
5593 |
16 |
1181 |
102 |
49 |
1394761 |
10404 |
2401 |
120462 |
57869 |
4998 |
17 |
922 |
100 |
65 |
850084 |
10000 |
4225 |
92200 |
59930 |
6500 |
18 |
1281 |
103 |
54 |
1640961 |
10609 |
2916 |
131943 |
69174 |
5562 |
19 |
1333 |
113 |
59 |
1776889 |
12769 |
3481 |
150629 |
78647 |
6667 |
20 |
1632 |
124 |
36 |
2663424 |
15376 |
1296 |
202368 |
58752 |
4464 |
21 |
635 |
95 |
70 |
403225 |
9025 |
4900 |
60325 |
44450 |
6650 |
22 |
949 |
102 |
64 |
900601 |
10404 |
4096 |
96798 |
60736 |
6528 |
23 |
788 |
112 |
48 |
620944 |
12544 |
2304 |
88256 |
37824 |
5376 |
24 |
1728 |
124 |
30 |
2985984 |
15376 |
900 |
214272 |
51840 |
3720 |
25 |
1773 |
116 |
58 |
3143529 |
13456 |
3364 |
205668 |
102834 |
6728 |
26 |
1679 |
118 |
48 |
2819041 |
13924 |
2304 |
198122 |
80592 |
5664 |
27 |
1085 |
100 |
69 |
1177225 |
10000 |
4761 |
108500 |
74865 |
6900 |
28 |
1214 |
99 |
58 |
1473796 |
9801 |
3364 |
120186 |
70412 |
5742 |
29 |
1422 |
107 |
49 |
2022084 |
11449 |
2401 |
152154 |
69678 |
5243 |
30 |
523 |
87 |
76 |
273529 |
7569 |
5776 |
45501 |
39748 |
6612 |
31 |
1025 |
109 |
59 |
1050625 |
11881 |
3481 |
111725 |
60475 |
6431 |
32 |
1083 |
106 |
74 |
1172889 |
11236 |
5476 |
114798 |
80142 |
7844 |
33 |
1466 |
113 |
54 |
2149156 |
12769 |
2916 |
165658 |
79164 |
6102 |
34 |
1642 |
123 |
36 |
2696164 |
15129 |
1296 |
201966 |
59112 |
4428 |
35 |
387 |
82 |
75 |
149769 |
6724 |
5625 |
31734 |
29025 |
6150 |
36 |
704 |
104 |
51 |
495616 |
10816 |
2601 |
73216 |
35904 |
5304 |
37 |
1177 |
112 |
35 |
1385329 |
12544 |
1225 |
131824 |
41195 |
3920 |
38 |
1792 |
116 |
47 |
3211264 |
13456 |
2209 |
207872 |
84224 |
5452 |
39 |
2072 |
106 |
33 |
4293184 |
11236 |
1089 |
219632 |
68376 |
3498 |
40 |
1178 |
120 |
28 |
1387684 |
14400 |
784 |
141360 |
32984 |
3360 |
41 |
1304 |
105 |
58 |
1700416 |
11025 |
3364 |
136920 |
75632 |
6090 |
42 |
1308 |
114 |
32 |
1710864 |
12996 |
1024 |
149112 |
41856 |
3648 |
43 |
1416 |
107 |
58 |
2005056 |
11449 |
3364 |
151512 |
82128 |
6206 |
44 |
1185 |
115 |
44 |
1404225 |
13225 |
1936 |
136275 |
52140 |
5060 |
45 |
1220 |
96 |
68 |
1488400 |
9216 |
4624 |
117120 |
82960 |
6528 |
46 |
1311 |
104 |
64 |
1718721 |
10816 |
4096 |
136344 |
83904 |
6656 |
47 |
1288 |
108 |
25 |
1658944 |
11664 |
625 |
139104 |
32200 |
2700 |
48 |
918 |
102 |
54 |
842724 |
10404 |
2916 |
93636 |
49572 |
5508 |
49 |
809 |
102 |
70 |
654481 |
10404 |
4900 |
82518 |
56630 |
7140 |
50 |
1188 |
120 |
19 |
1411344 |
14400 |
361 |
142560 |
22572 |
2280 |
Сумма |
61641 |
5441 |
2526 |
81910843 |
596263 |
138188 |
6810220 |
3000258 |
269771 |
Среднее значение |
1232,82 |
108,82 |
50,52 |
1638216,86 |
11925,26 |
2763,76 |
136204,4 |
60005,16 |
5395,42 |
|
118371,7076 |
83,4676 |
211,4896 |
– |
– |
– |
– |
– |
– |
|
344,0519 |
9,1361 |
14,5427 |
– |
– |
– |
– |
– |
– |
Построим уравнение множественной регрессии.
Для нахождения параметров уравнения регрессии в данном случае необходимо решить следующую систему нормальных уравнений:
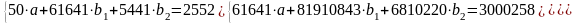 .
.
Решая ее методом определителей, получим:
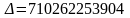 ;
;
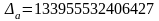 ;
;
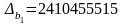 ;
;
 .
.
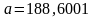 ;
;
 ;
;
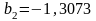 .
.
Уравнение множественной регрессии выглядит следующим образом:
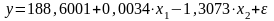 .
.
Оно показывает, что:
при увеличении
только собственных оборотных средств
 (при неизменном
(при неизменном
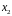 )
на 1 млн. руб. дебиторская
задолженность
)
на 1 млн. руб. дебиторская
задолженность
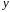 увеличивается в среднем на 0,0034 млн.
руб.;
увеличивается в среднем на 0,0034 млн.
руб.;
при увеличении только балансовой прибыли (при неизменном ) на 1 млн. руб. дебиторская задолженность уменьшится в среднем на 1,3073 млн. руб.
Рассчитаем частные коэффициенты эластичности.
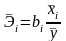 .
.
Вычисляем:
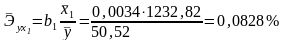
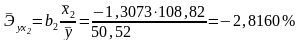
Т.е. увеличение только собственных оборотных средств на 1% увеличивает в среднем дебиторскую задолженность на 0,0828%; увеличение только балансовой прибыли на 1% уменьшает в среднем дебиторскую задолженность на 2,8160%. Таким образом, подтверждается большее влияние на результат фактора , чем фактора .
Найдём стандартизованные коэффициенты регрессии (-коэффициенты).
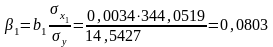
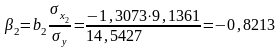
Уравнение множественной регрессии в стандартизованном масштабе:
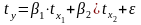
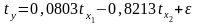
Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что балансовая прибыль оказывает большее влияние на дебиторскую задолженность, чем собственные оборотные активы.
Найдем значения парных коэффициентов корреляции:

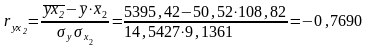
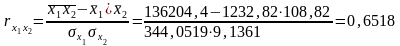
Значения
парных коэффициентов корреляции
указывают на высокую связь дебиторской
задолженности
с балансовой прибылью
и на заметную связь с собственными
оборотными средствами
.
В то же время межфакторная связь
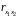 заметная.
заметная.
Теперь
рассчитаем совокупный коэффициент
корреляции
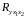 .
Для этого сначала найдем определитель
матрицы парных коэффициентов корреляции:
.
Для этого сначала найдем определитель
матрицы парных коэффициентов корреляции:
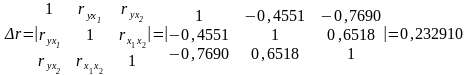
и определитель матрицы межфакторной корреляции:
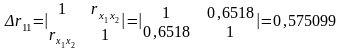 .
.
Коэффициент множественной корреляции:
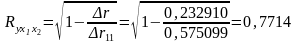 .
.
Множественный коэффициент детерминации определим как квадрат множественного коэффициента корреляции.

Т.е. можно сказать, что 59,50% вариации результата объясняется вариацией представленных в уравнении признаков.
Находим линейные коэффициенты частной корреляции:
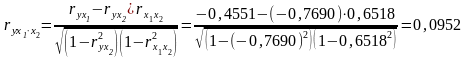
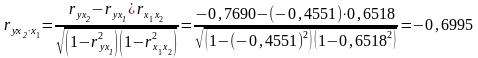
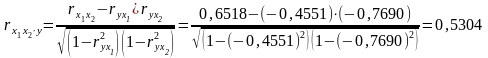
Т.е. можно сделать вывод, что фактор оказывает более сильное влияние на результат, чем признак .
Теперь рассчитаем средние ошибки коэффициентов регрессии по формуле:
 .
.
 ;
;
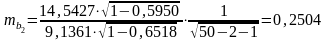 .
.
Рассчитаем t-критерий Стьюдента для каждого коэффициента регрессии:
 ;
;
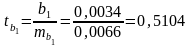 ;
;
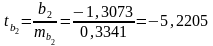 .
.
Сравнив
рассчитанные значения t-критериев
с табличным (α=0,05; df=50-2-1=47;
tтабл=2,01)
получаем, что параметр
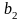 является статистически значимым, а
параметр
является статистически значимым, а
параметр
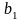 является статистически незначимым.
является статистически незначимым.
Оценим надежность уравнения регрессии в целом и показателя связи с помощью -критерия Фишера. Фактическое значение -критерия
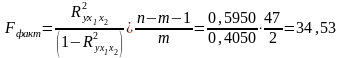
Табличное
значение
-критерия
при пятипроцентном уровне значимости
(α=0,05,
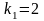 ,
,
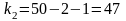 ):
Fтабл=3,18
):
Fтабл=3,18
Так как Fфакт> Fтабл, то уравнение признается статистически значимым.
Общий вывод
состоит в том, что множественная
модель с факторами
и
с
 содержит неинформативный фактор
.
содержит неинформативный фактор
.
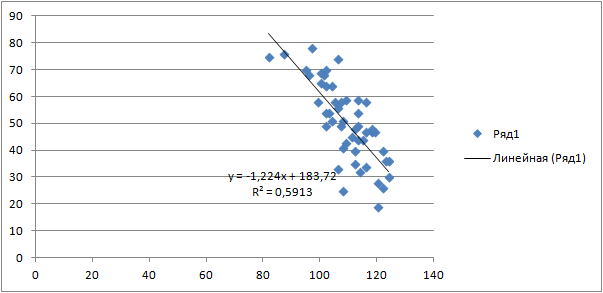
Если исключить фактор , то можно ограничиться уравнением парной регрессии:
 ,
,
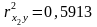 .
.