Самостійна робота №3
ТРАНСПОРТНА ЗАДАЧА ЗА КРИТЕРІЄМ ЧАСУ НА ПЕРЕВЕЗЕННЯ
Мета заняття: вивчення методу потенціалів для рішення транспортної задачі за критерієм часу на перевезення.
Стисла теоретична довідка
При перевезеннях вантажів, що швидко псуються, та деяких будівельних матеріалів виникає необхідність доставити вантаж у найбільш стислий термін. Математична постановка транспортної задачі за критерієм часу полягає у наступному.
Нехай
є m
пунктів зосередження вантажу (або
пунктів виробництва)
,
,
...,
,
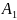в яких розміщено однорідний вантаж
у кількості
,
,
...,
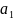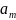одиниць. Цей вантаж повинен бути
доставлений у n
пунктів споживання
,
,
...,
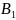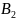з обсягом попиту відповідно
,
,
...,
.
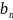Передбачається, що можливе транспортування
з кожного пункту постачання до кожного
пункту споживання. Задані тривалості
транспортування
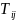на доставку одиниці вантажу з пунктів
до пунктів
(
;
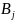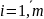j=
).
Задача полягає у складанні такого плану перевезень, який забезпечує виконання наступних умов:
запаси кожного постачальника повинні бути повністю вивезені;
попит всіх пунктів споживання повинен бути задовільнений за рахунок розподілу всього запасу вантажів, тобто
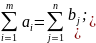
мінімізувати максимальну тривалість транспортування вантажу.
Умови транспортної задачі подають у вигляді таблиці, що аналогічна таблиці вихідних даних транспортної задачі лінійного програмування за критерієм вартості. У правих верхніх кутах клітинок вказується тривалість транспортування вантажу між відповідними пунктами.
Поставлена задача не є задачею лінійного програмування, а є задачею на пошук мінімаксу. При її рішенні допустимим є складання планів, що є опорними і не опорними, виродженими і не виродженими.
Алгоритм рішення задачі полягає у виконанні наступних дій:
скласти початковий план перевезень (методом північно-західного кута, мінімальної вартості чи подвійної переваги);
найти завантажену клітинку з максимальним значенням тривалості перевезень. Обвести це значення кружечком. Виключити з подальшого аналізу порожні клітинки матриці, де значення тривалості перевезень перевищує це значення, проставляючи у цих клітинках хрестики;
побудувати розвантажувальний контур. Розвантажувальний контур є замкненим контуром, для якого виконуються наступні умови:
до його вершин входять клітинки, не позначені хрестиком;
вершинах циклу по черзі проставляються знаки “+” та “–“, починаючи з клітинки з кружечком, в якій проставляється знак “–“;
клітинки, позначені знаком “+”, є завантаженими;
визначити, чи є завантаження клітинки з кружечком найменшим у порівнянні з завантаженням клітинок, позначених у розвантажувальному контурі знаком “–”. Якщо воно є найменшим, то значення цього завантаження відняти від завантажень клітинок, позначених знаком “–“ та додати до завантажень клітинок, позначених знаком “+“.
Дії алгоритму повторюють, доки не буде отримане оптимальне рішення задачі (незмога побудувати розвантажувальний контур).