Определение предельного угла отключения короткого замыкания

Время отключения КЗ определяется несколькими факторами:

1. Необходимо обеспечить работоспособность электрооборудования, которое увеличится с уменьшением времени КЗ;

2. Время определяется временем срабатывания релейной защиты;

3. Селективностью или зоной нахождения аварии (расположение мета повреждения до места защиты);

4. Необходимостью сохранения устойчивости электроэнергии системы;

Под селективностью понимают срабатывание ее в зоне действия данной защиты и ее несрабатывании вне зоны действия.

В аварийном режиме схема замещения системы изображается с использованием схем прямой последовательности при различных видах аварии:

1. Трёхфазное металлическое КЗ ;

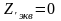2. Однофазное металлическое КЗ ;

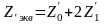3. Межфазное металлическое КЗ ;

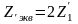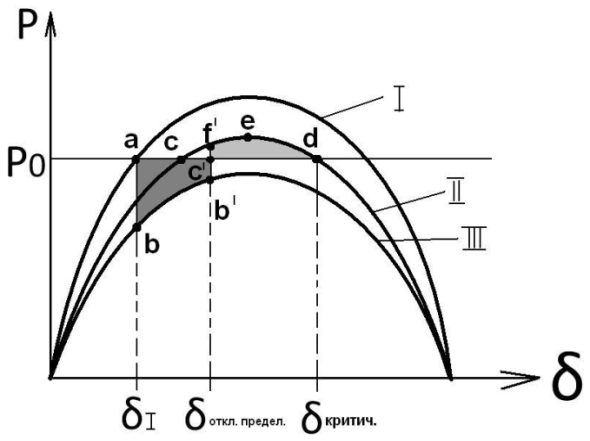
Для обеспечения устойчивой работы электроэнергетической системы мы дополняем характеристику мощности аварийных режимов (кривая III), в котором сопротивление связи Х, определяется условиями аварии.

Предельное время отключения КЗ характеризуется точкой b’, определяющей равенство площадки ускорения аb’bс’а и площадки торможения c’defc’

Равенство площадей записывается в следующем виде:

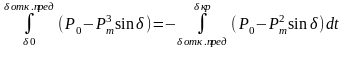
После преобразования получим:

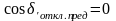
Лекция №8. Метод последовательных интервалов.

Является упрощенным решением дифференциального уравнения описывающего вращение ротора генератора. Решением этого уравнения является зависимость угла δ от времени при переходном электромеханическом процессе. Уравнение относительного движения синхронной машины при небалансе момента турбины и электромагнитного момента может быть записано в следующем виде:

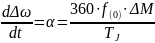
Где , 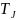-постоянная инерции ротора.

Решение записанного уравнения означает определение зависимости .

При расчетах относительного движения ротора, происходящего со скоростью много меньше синхронной, полагают, что мощность численно равна моменту. Тогда:

В методе последовательных интервалов, предполагают, что задача уже решена и подлежащие нахождению зависимости изображаются в следующем виде:

Частота вращения ротора генератора записывается в ви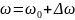де:

, где -синхронная скорость, -угловая скорость относительного движения ротора (относительно синхронной).

Производная по времени от относительной скорости вращения ротора равна ускорению ротора:

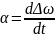
Производная по времени от угла δ это есть относительная скорость вращения ротора генератора:

Следствием этих выражений является запись:

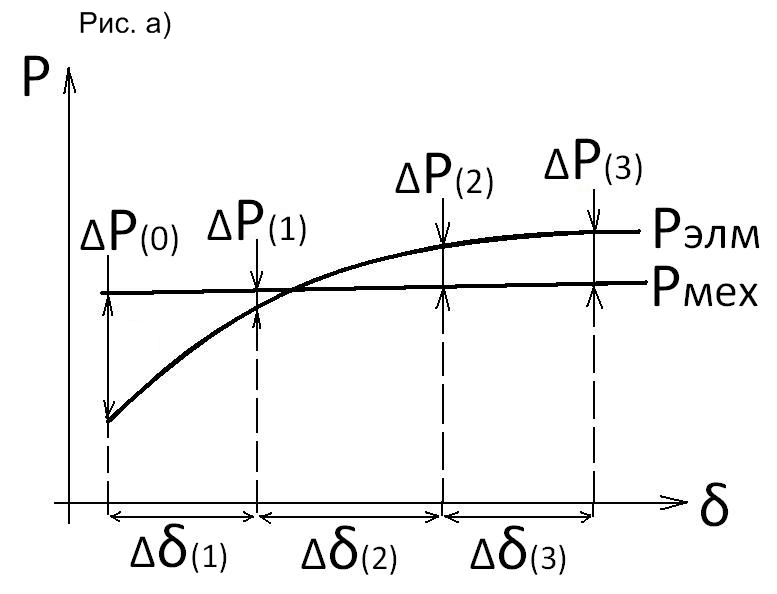
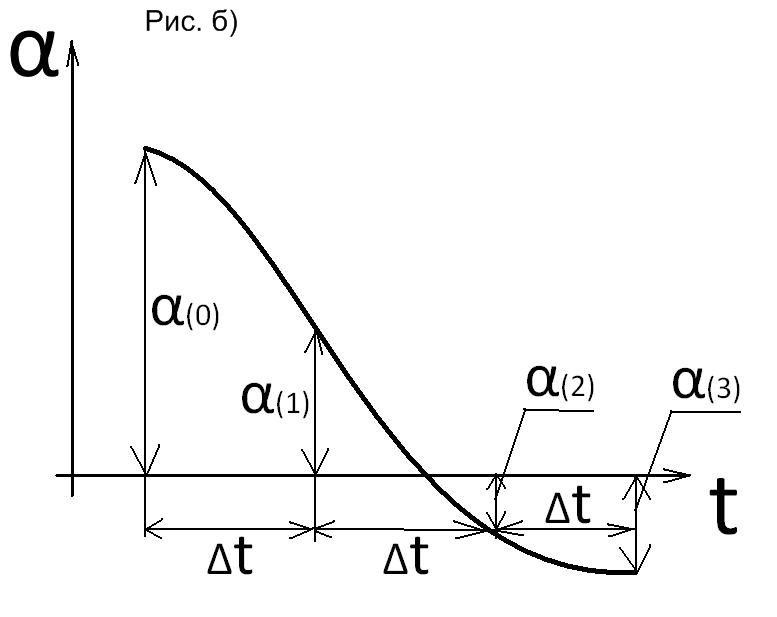
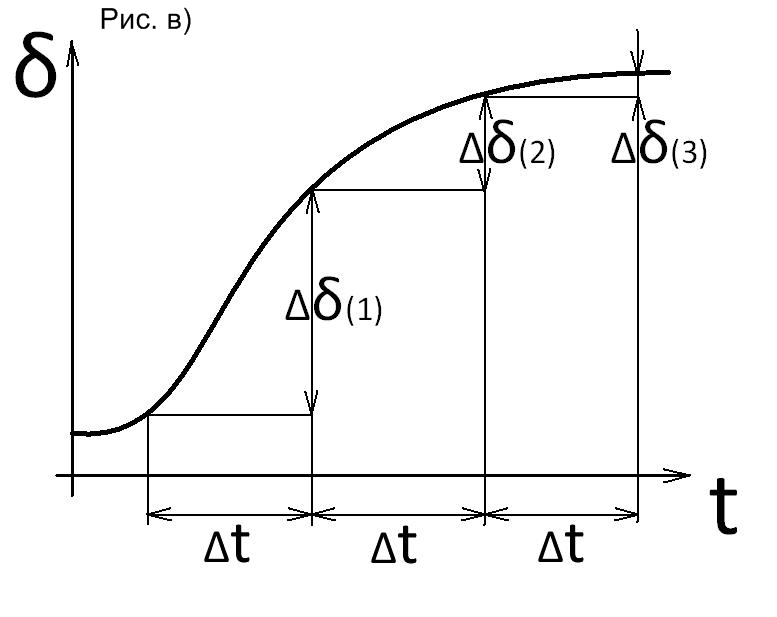
Разобьем весь процесс на малые интервалы времени Δt и будем рассматривать его последовательно от интервала к интервалу. Выбирая одинаковые интервалы по времени (рис. б и в) будем иметь неодинаковые интервалы по углу (рис. а).

Каждый интервал характеризуется определенными значениями начальных и конечных величин угла, скорости, ускорения и средними значениями скорости и ускорения действующими в данном интервале. Начальные значения этих величин в последних интервалах выбирают такой, чтобы на его протяжении можно было считать ускорение неизменным. Обычно Δt =0,02-0,1 сек. В первом интервале начальная скорость равна нулю, и при постоянном ускорении равна α (рис.б) изменение угла будет происходить по закону равноускоренного движения. Приращение угла к концу интервала составит

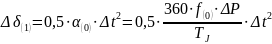
Приращение мощности изменяется при изменениях угла и времени. Зная приращение Δt и приращение 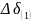можно определить (по аналитической зависимости электрической мощности от угла) - небаланс мощности в конце первого или в начале второго интервала. В конце первого интервала мы нашли угол ,который является условием начала движения во втором интервале. Ускорение на втором интервале равно:

Соответственно во втором интервале изменение угла δ зависит от скорости 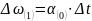, которую получил ротор в первом интервале и ускорения .

Приращение угла δ во втором интервале:

Значение скорости на протяжении первого интервала непостоянно, ее среднее значение определяется:

Тогда

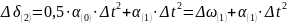
Аналогично получаются выражения для приращения угла в третьем, четвертом и последующих интервалах, которые записываются в следующем виде:

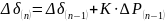
Лекция №9

Метод малых колебаний

Метод малых колебаний - это метод исследования статической устойчивости простейшей нерегулируемой электроэнергетической системы.

Установившийся режим электроэнергетической системы не означает неизменность параметров его режима. Такая система имеет огромное количество нагрузок, которые стохастически изменяются. В связи с этим на валу генераторов системы появляются случайные малые моменты 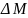, уменьшающие или увеличивающие моменты на валах этих генераторов и смещающие их роторы на некоторые углы . Примем, что моменты равны приращению мощности 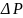. Предположим, что ЭДС генератора постоянна (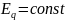 ), т.е. не учитывается регулирование генератора в переходном процессе. Приближенно можно написать: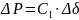

Где

С учетом допущений ; U ; 𝜟𝛿,𝜟ω,𝜟Р-малы, основное уравнение малых колебаний запишется в следующем виде: 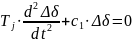. Решение дифференциального уравнения ищется в виде 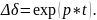Если при анализе уравнения учитывается демпферный момент, то получим следующее уравнение:

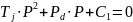
Корни этого квадратного уравнения записываются в виде:

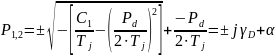
Где 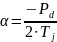- это декремент затухания

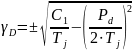– это частота колебаний относительного приращения угла 𝛿.

Решение исходного уравнения имеет следующий вид:

Определив постоянные интегрирования С₁ и С₂ из начальных условий получаем зависимость 𝜟𝛿=f(t). При изучении малых колебаний системы не строят эту зависимость в численном виде, а ограничиваются выяснением ее характера, т.е. определяют будет ли изменение угла апериодическим или колебательным (затухающим или возрастающим). Характер процесса устанавливается следующими способами:

1. Нахождение численных значений корней характеристического уравнения.

2. Определение знака вещественных частей корней без нахождения численных значений.

Рассмотрим зависимость между расположением корней на комплексной плоскости и характером процесса изменения угла 𝜟𝛿 во времени. Очевидно, что появление положительной вещественной части в корне уравнения будет указывать на непрерывное увеличение угла 𝜟𝛿, т.е. на неустойчивость; при отрицательных вещественных частях комплексных корней, характер процесса будет затухающим апериодически или колебательно. При обращении действительной и мнимой части в ноль, в полученной системе начальное отклонение угла 𝜟𝛿 остается неизменным. Обращение в ноль действительных частей корней указывает на появление незатухающих колебаний.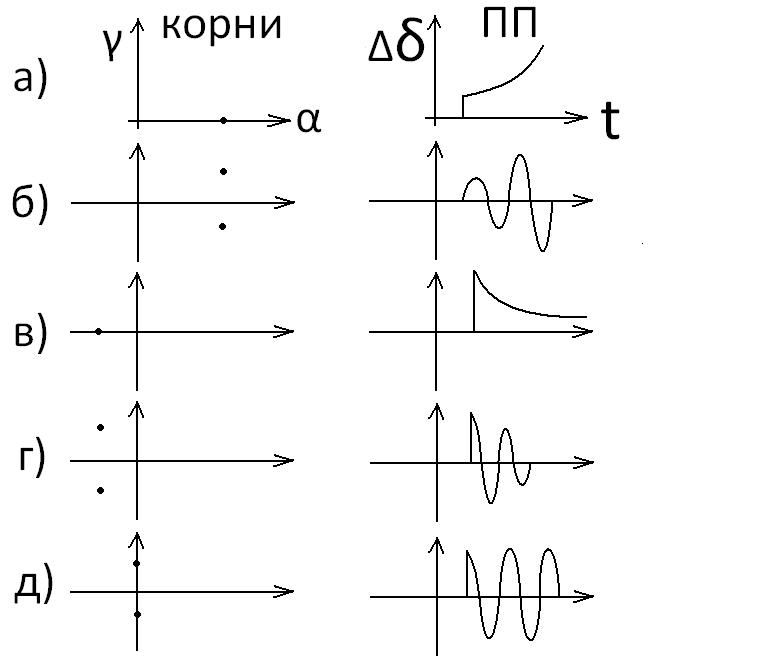

Рассмотрим уравнения для частоты колебаний угла 𝜟𝛿. При С₁>0 система всегда устойчива. При оба корня будут действительные и отрицательные, и процесс будет иметь характер, изображенный на рисунке в).

При обратном соотношении оба корня будут комплексными с отрицательными вещественными частями и характер процесса будет таким как показано на рисунке г).

При С₁<0 соотношение между 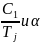не влияет на характер процесса. Один корень всегда будет действителен и положителен (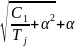 ), а другой отрицателен ( ). Первый корень соответствует либо рисунку а) или в), а второй всегда в).

При С₁=0 появляется один нулевой корень и один корень равный ( ). Наличие нулевого корня указывает на критический случай, когда для выяснения действительного поведения системы необходимо проводить дополнительные исследования, т.к. знак единичного толчка сможет приводить как к устойчивому поведению системы так и к неустойчивому.

Лекция № 10. Регулирование возбуждения и скорости агрегатов электрической системы.

Агрегаты электрических систем (генераторы и вращающие их турбины) должны обеспечивать определенное качество нормального режима системы. Это достигается поддерживанием в определенных границах с помощью регулирования тех параметров режима, которыми это качество количественно характеризуется.

Регуляторы возбуждения осуществляют регулирование напряжения генератора, а регуляторы частоты поддерживают в заданных пределах частоту в системе.

Регуляторы должны действовать при переходных режимах, обеспечивая качество переходных процессов. Качество переходного процесса связано с обеспечением его устойчивости. Упрощенно, рассмотрение процессов регулирования можно отобразить моделью, в которой человек следя за показаниями приборов (например, вольтметром) осуществляет регулирование.

Процесс регулирования заключается в том, чтобы передвигая рукоятку реостата, регулирующего ток возбуждения, поддерживать такое напряжение на выходе генератора, чтобы разность номинального напряжения и выходного напряжения не превосходила некоторой величины ∆U.

Слежение за величиной разности ∆U осуществляется или прерывисто (с зоной нечувствительности) или непрерывно (пропорционально).

В первом случае (прерывисто) человек не реагирует на малые изменения напряжения и регулирование начинается когда разность ∆U достигает величины ∆U0

Это регулирование называется регулированием с зоной нечувствительности. Если регулирующее воздействие начинается при любом малом изменении регулируемой величины и далее пропорционально ему меняет свою интенсивность, то осуществляется пропорциональное регулирование. График пропорционального регулирования изображен на рисунке:

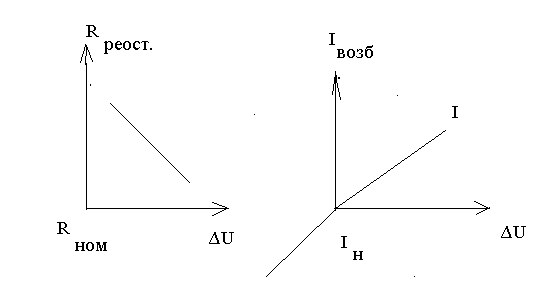
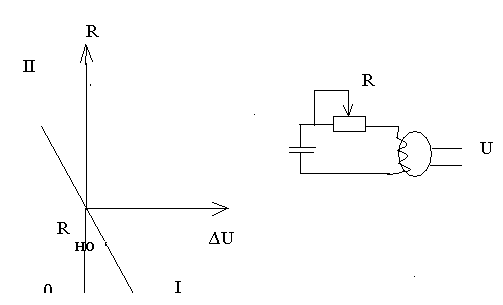
Предположим, что реостат, регулирующий напряжение, имеет пружину жёсткостью С и обладает механической инерцией М. В процессе регулирования инерцию и жёсткость пружины приходится преодолевать регулятору (например, человеку), создающего силу, пропорциональную величине

F=K×∆U

Если заменить человека автоматом, то оно должно содержать измерительное устройство, обнаруживающую ошибку ∆U и регулятор, создающий силу F=K×∆U. Величину K называют коэффициентом усиления, а процесс слежения за прибором во время регулирования, устранения перерегулирования и колебаний за счёт обратных регулирующих воздействий, называют процессом обратной связи или просто обратной связью. Эффективность обратной связи характеризуется коэффициентом K _ос.

Очевидно, что можно обеспечить увеличение напряжения до заданного уровня при малом ∆U, имея достаточно большой коэффициент усиления. Трудности регулирования при этом увеличиваются, так как необходимо соизмерять большую силу с малой величиной ∆U, получающейся как разность двух больших величин. Необходимо определённое время, чтобы человек натренировался в таком регулировании и вёл его устойчиво.

Для устойчивого регулирования человеку необходимо реагировать не только на отклонения, но и на скорость изменения отклонения. Соответственно, автомату также необходимо придать определённые свойства, чтобы он справлялся со своей задачей.

Лекция №10-1.

Тема: «Применение способа площадей при анализе действия автоматического регулирования».

Рассмотрим применение способа площадей при анализе эффективности увеличения возбуждения, применяемого для улучшения динамической устойчивости.

Увеличение тока возбуждения позволяет увеличивать амплитуду угловой характеристики выдаваемой генератором мощности во время аварийного и послеаварийного режимов и уменьшать этим влияние сброса нагрузки и вылета угла δ, способствуя сохранению устойчивости.

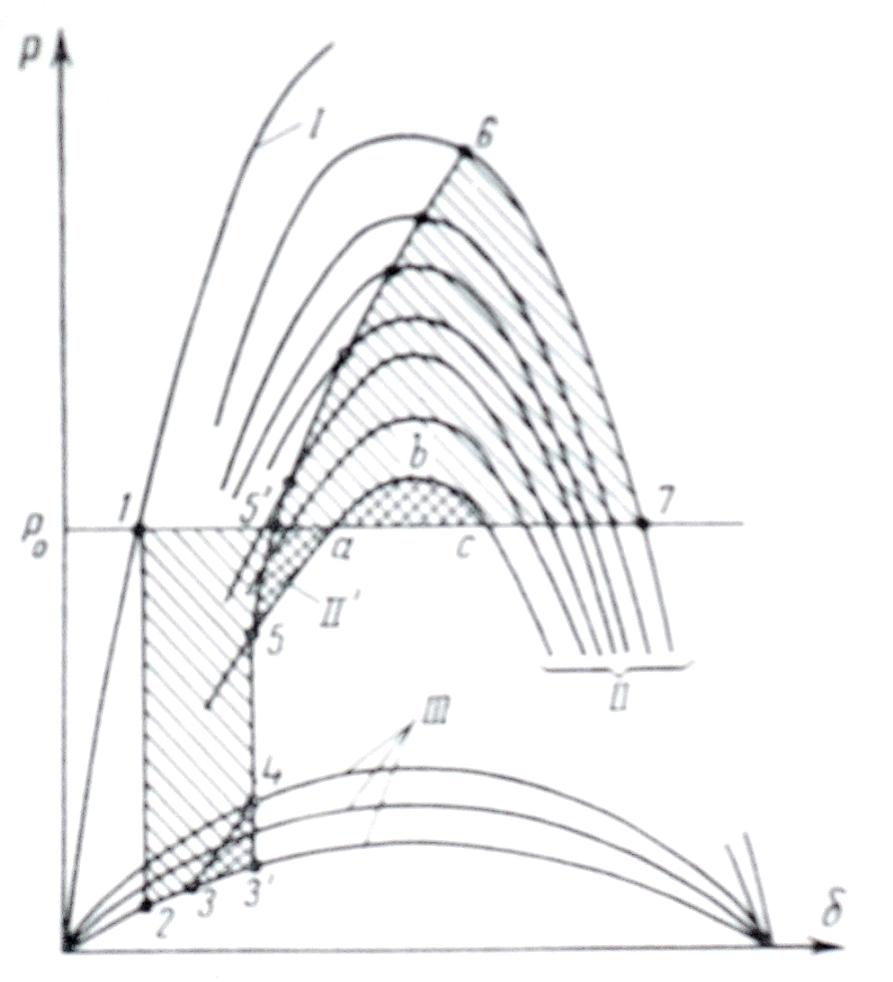
I – характеристика нормального режима;

II' – характеристика послеаварийного режима без форсирования;

II – группа характеристик послеаварийного режима при разных значениях тока возбуждения;

III – характеристика аварийного режима, где участки:

2-3 – запаздывание форсирования,

3-4 – форсирование возбуждения во время аварии,

5-5'-6 – форсирование возбуждения в послеаварийном режиме,

6-7 – угловая характеристика при постоянном значении тока возбуждения.

На рисунке представлены характеристики переходного процесса при КЗ и отключении КЗ, когда возбуждение форсируется или отсутствует. Если форсировка возбуждения отсутствует, то при КЗ и его отключении энергия при ускорении ротора определяется площадкой 1-2-3-3'-4-5-a-5'-1.

Энергия при торможении определяется площадкой a-b-c. Энергия торможения площадки a-b-c много меньше площадки ускорения - это означает неустойчивость системы. При форсировании возбуждения ток возбуждения начинает увеличиваться и площадка ускорения уменьшается и описывается координатами 1-2-3-4-5-5'-1. Максимальная площадка торможения при учете форсировки возрастает и описывается координатами 5'-6-7-5'. Участок 5'-6 соответствует продолжающемуся форсированию тока возбуждения, достигающему наибольшего допустимого значения в точке 6.

Из приведенных характеристик видно, что при сбросе нагрузки, вызванном КЗ, необходимо как можно скорее и значительнее увеличить ток возбуждения генератора. Однако увеличить ток возбуждения полезно лишь, пока увеличивается угол δ, при этом увеличивающийся ток возбуждения создает дополнительный тормозящий момент, способствующий сохранению устойчивости. Лишь угол δ, достигнув максимального значения, начал уменьшаться, нет надобности продолжать увеличивать или поддерживать ток возбуждения.

При уменьшении угла δ ток возбуждения необходимо снижать. Если его не будут снижать, то возникнут большие колебания угла, и генератор может выпасть из синхронизма во втором цикле качаний.

Тест

I:

S: Отметьте правильный ответ. При правильном управлении током возбуждения АРВ генератора

+: ток возбуждения растет при увеличении угла системы и снижается при уменьшении угла системы

-: ток возбуждения растет при уменьшении угла системы и снижается при росте угла системы

I:

Характеристики асинхронных двигателей

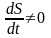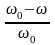Статические и динамические характеристики асинхронных и синхронных двигателей различны. Это обусловлено появлением свободных токов при быстром изменении скольжения ( , где S= ). У асинхронных двигателей скольжение отлично от нуля, а у синхронных равно нулю.

При рассмотрении устойчивости работы обоих типов двигателя используют зависимость электрической мощности потребляемой двигателем в зависимости от величины скольжения.

Рисунок 1

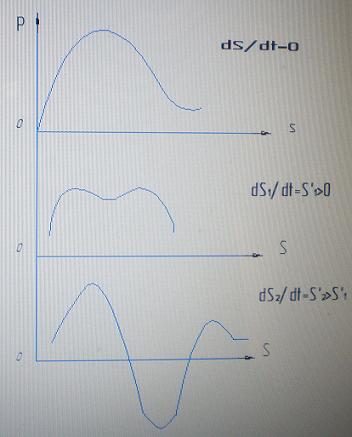
На рисунке 1 изображена электрическая мощность, потребляемая асинхронным двигателем, в зависимости от величины скорости изменения скольжения. Если скорость изменения скольжения мала, то при анализе режима двигателя приближенно можно получать динамические характеристики (ds/dt><0) на основе ряда статических характеристик (ds/dt=0).

Запишем количественные соотношения между параметрами режима на основе схемы замещения асинхронного двигателя. Для упрощения пренебрегаем активным сопротивлением цепи статора.

Рисунок 2

Где Х_S – суммарное сопротивление рассеяния обмоток статора и ротора;

Х_µ - сопротивления намагничивания статора;

R₂ - приведенное сопротивление ротора и статора.

Активная мощность, потребляемая нагрузкой, т. е. вращающий момент двигателя определяется мощностью машин приводимых во вращение и их характеристиками.

М_мех= f( ω)

Для упрощения примем, что механическая мощность не зависит от скольжения. Тогда, можно записать следующее соотношение:

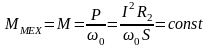
Активная мощность как функция напряжения скольжения находится из схемы замещения следующим образом:

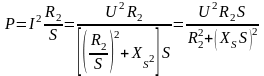
Рисунок 3

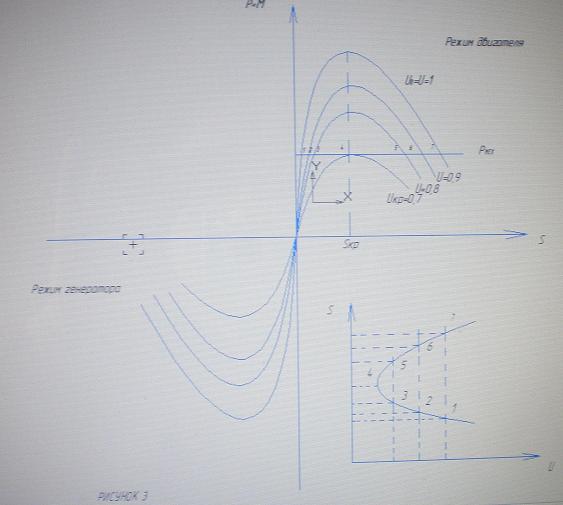
На рисунке 3 изображена зависимость между мощностью, напряжением и скольжением. При данной механической нагрузке Р_мех, у каждого двигателя есть определенный критический режим. Напряжение U_кр и скольжение S_кр, при котором этот режим наступает, называют критическими. Максимальный момент, который может развивать двигатель в критическом режиме, равен механическому моменту рабочей машины. При дальнейшем понижении напряжения работа невозможна, поскольку электрический момент оказывается меньше механического момента.

Значение максимального момента и критического скольжения можно определить, продифференцировав выражение мощности по скольжению и приравняв нулю:

.

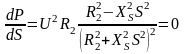
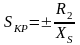“- ” – режим генератора;

“ +” – режим двигателя.

При этом скольжении находим значение максимальной мощности, т.е подставляем в формулу активной мощности и получаем:

.

Величина критического скольжения определяется через номинальное скольжение S₀ и кратность максимального момента b₀ :

;

.

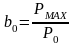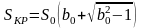Значение S₀ в основном зависит от мощности двигателя. Для малой мощности ( несколько кВт) она составляет 5 %, при средней мощности S₀ = 2% и у очень крупных двигателей ( сотни кВт) уменьшается до 1 %.

Используя понятия S_кр и P_max, перепишем выражения для мощности, которыми часто пользуются при расчетах электрических приводов:

.

Работа двигателя при положительном значении ( точки 1,2,3) устойчива, при отрицательном - неустойчива. Таким образом, у асинхронного двигателя имеется лишь одна область устойчивой работы между синхронной скоростью ( S=0) и критическим скольжением. Область между критическим скольжением и скольжением S=1, оказывается неустойчивой.

В нормальных условиях двигатель работает на устойчивой части своей характеристики, при значении S< S_KP. Однако, при снижении напряжения или увеличении механического вращающего момента, двигатель может оказаться в критическом режиме. При дальнейшем снижении напряжения, точка, характеризующая режим, перейдет на спадающую часть характеристики, двигатель тормозится, ток и реактивная мощность резко растут, а затем двигатель останавливается или опрокидывается. Обычно двигатели работают с большим запасом устойчивости. Их рабочее скольжение значительно меньше критического, а максимальный вращающий момент много больше рабочего ( 50-70%). В этих условиях, колебания напряжения не опасны с точки зрения устойчивости двигателей, и только очень большие снижения напряжения на их шинах (20-40%) приводят к опрокидыванию двигателей.

Переходные процессы в узлах нагрузки.

Часть электроэнергетической системы, непосредственно осуществляющая снабжение электроэнергией потребителей, называется системой электроснабжения, и содержит питающие и распределительные сети, трансформаторы, компенсирующие устройства и устройства, в которых электроэнергия используется в производственных или бытовых целях.

Места подключения отдельных систем электроснабжения к высоковольтным сетям электрических систем, называются узлами нагрузок.

В нормальных режимах, при малых возмущениях, проверяют статическую устойчивость синхронных двигателей, синхронных компенсаторов и больших групп асинхронных двигателей, которые, имея мощность, соизмеримую с мощностью питающих их генераторов, могут оказаться неустойчивыми. Эта неустойчивость проявляется в виде специфического явления, называемого лавиной напряжения.

Пуски двигателей, резкие колебания момента на их валу приводят к изменениям величины и фазы напряжения в узлах нагрузки. Эти отклонения не должны выходить из допустимых пределов.

Влияние резких изменений режима двигателя проявляется в распределительных сетях в виде колебаний напряжения. Медленное изменение режима двигателя, связанное с технологическими процессами, в которых эти двигатели участвуют, отражается на уровне напряжения в питающих сетях. Нарушения режима типа короткого замыкания в элементах питательных сетей, отключение и повторное включение синхронных двигателей, самозапуск асинхронных двигателей после перерыва питания, самовозбуждение и самораскачивание двигателей при работе на емкостном сопротивлении, могут существенно сказаться на режиме всей системы электроснабжения. Поэтому переходные процессы в элементах системы элекроснабжения рассматриваются с точки зрения обеспечения надежности всей системы электроснабжения.

«Лавиной» напряжения называется явление, связанное с неустойчивостью групп асинхронных двигателей. Асинхронные двигатели имеют большой запас устойчивости и обеспечение статической устойчивости отдельных двигателей не вызывает затруднений. Коэффициент запаса отдельного двигателя составляет 1,5-1,7 о.е.(это отношение максимального вращающего момента к рабочему). Если группа двигателей питается от генератора соизмеримой с ним мощности, то напряжение на шинах двигателей зависит от его режима (скольжения). Условия нарушения устойчивости двигателя получаются в этом случае иными, чем для одиночного двигателя.

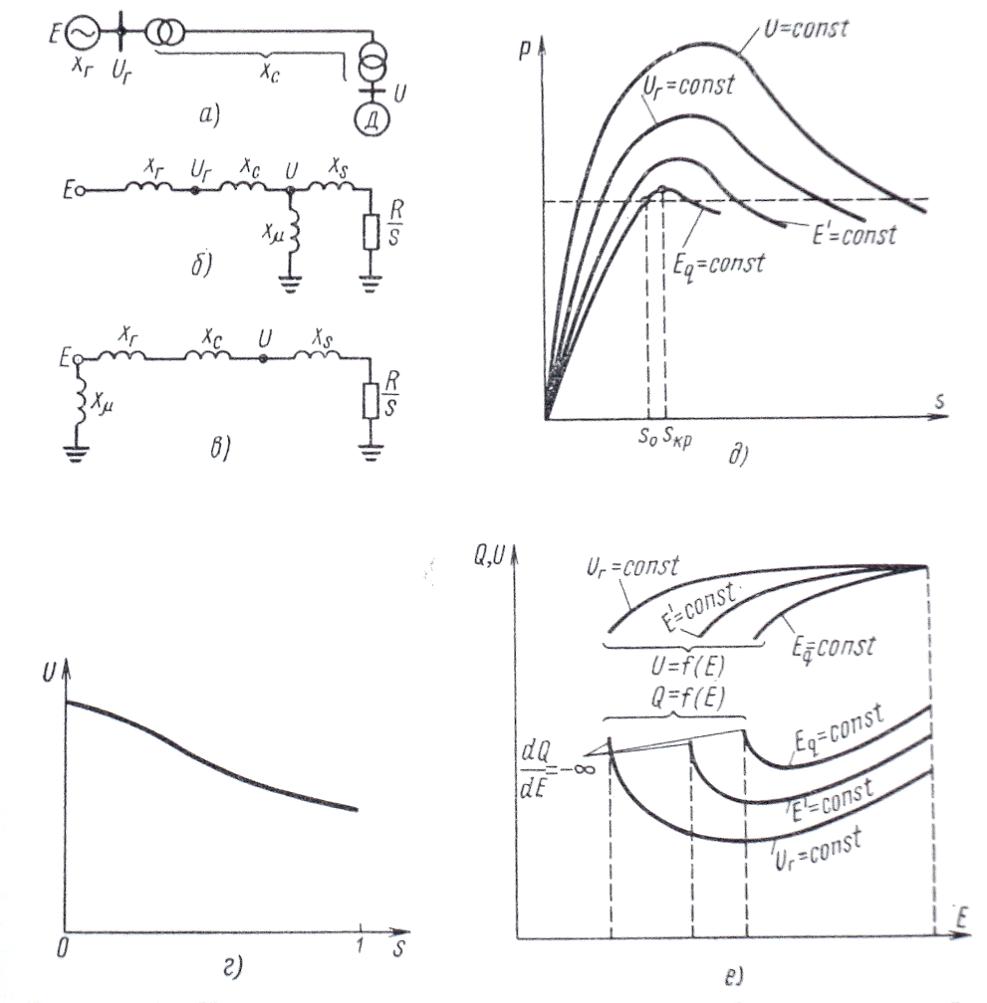
На рис.а сопротивление генератора x_Г, сопротивление сети x_С, сопротивление x_S соизмеримы по величине. Изобразим схему замещения в виде рис.б и упростим ее переносом сопротивления x_μ к точке приложения ЭДС Е (рис.в). Из схемы видно, что напряжение на шинах двигателя будет падать с ростом скольжения и, соответственно, с ростом тока. Вращающий момент двигателя (мощность, потребляемая двигателем) удобно вычислять не по изменяющемуся напряжению U=f(S) на зажимах двигателя, а по неизменному значению E_Г. Максимальный вращающий момент будет:

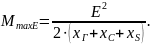
Величина , определенная при E=const., будет значительно меньше, чем определенная при условии U=const. Это отображается на рис. д и записывается в виде выражения:

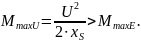
Записанное выражение для получено приближенно соответственно преобразованию схемы б в схему в. Это обстоятельство не меняет общих качественных закономерностей. Критическое скольжение, определяемое из выражения

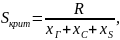
оказывается много меньше, чем 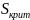двигателя, определявшееся ранее как . Отсюда следует, что опрокидывание двигателя, питающегося от генератора соизмеримой мощности может произойти при сравнительно небольших изменениях скольжения S и небольших снижениях ЭДС E, питающие эквивалентный двигатель и тем более при небольших изменениях напряжения U, зависящего от режима двигателя. Определение критических условий проводят исходя не из напряжения на зажимах двигателя, которое не является независимой переменной, а исходя из той ЭДС E_Г, которое в данных условиях можно считать не зависящей от изменения режима. Эта ЭДС при различном способе регулирования генератора будет различной. В случае нерегулируемого генератора это будет E_q (переходная ЭДС). В случае пропорционального регулятора возбуждения в качестве ЭДС выступает E_q', которая примерно равна E'. В случае регулятора сильного действия в качестве ЭДС выступает напряжение на зажимах генератора . Соответствие характеристики зависимости напряжения на зажимах двигателя от величины ЭДС и реактивной мощности, потребляемой двигателем, показано на рис.е. Из этих характеристик видно, что снижение ЭДС особенно в зоне, где производная 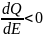, приводит к росту реактивной мощности, соответственному увеличению токов, потребляемых двигателями нагрузки и увеличению потерь напряжения питающей сети. Таким образом, вблизи режима опрокидывания двигателей процесс прогрессирующего снижения напряжения оказывается очень заметным.

Персонал станции не может судить непосредственно о росте токов роторов, статоров и скольжений двигателей, входящих в состав комплексной нагрузки в то время, когда они приближаются к опрокидыванию, но персонал может наблюдать резкое лавинообразное снижение напряжения. Поэтому этот процесс получил название лавины напряжения. Появлению лавины напряжения предшествуют режимы при недостаточно высоком возбуждении генераторов или при увеличении реактивных сопротивлений связи. Получающееся при этом снижение реактивной мощности, приходящей к потребителю, заставляет персонал систем считать причиной лавины напряжения так называемый «дефицит» реактивной мощности.

Количественное определение условий, в которых возникает лавина напряжения, и определение запаса устойчивости двигателей могут производиться исходя из схемы в также, как для единичного двигателя, только вместо напряжения будет фигурировать ЭДС и вместо сопротивления будет использоваться Более удобно вместо критерия устойчивости 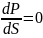или эквивалентного ему критерия 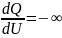воспользоваться вторичным критерием устойчивости:

Характеристики асинхронных двигателей

Статические и динамические характеристики асинхронных и синхронных двигателей различны. Это обусловлено появлением свободных токов при быстром изменении скольжения ( , где S= ). У асинхронных двигателей скольжение отлично от нуля, а у синхронных равно нулю.

При рассмотрении устойчивости работы обоих типов двигателя используют зависимость электрической мощности потребляемой двигателем в зависимости от величины скольжения.

P

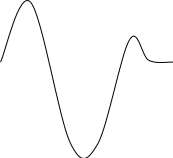
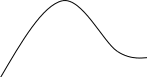Рисунок 1

0

0

0

S

S

S

dS₂/dt=S’₂>S’₁

dS₁/dt=S’₁>0

dS/dt=0

На рисунке 1 изображена электрическая мощность, потребляемая асинхронным двигателем, в зависимости от величины скорости изменения скольжения. Если скорость изменения скольжения мала, то при анализе режима двигателя приближенно можно получать динамические характеристики (ds/dt><0) на основе ряда статических характеристик (ds/dt=0).

Запишем количественные соотношения между параметрами режима на основе схемы замещения асинхронного двигателя. Для упрощения пренебрегаем активным сопротивлением цепи статора.

X_s

Рисунок 2

X_µ

r₂=R₂/S

Где Х_S – суммарное сопротивление рассеяния обмоток статора и ротора;

Х_µ - сопротивления намагничивания статора;

R₂ - приведенное сопротивление ротора и статора.

Активная мощность, потребляемая нагрузкой, т. е вращающий момент двигателя определяется мощностью машин приводимых во вращение и их характеристиками.

М_мех= f( ω)

Для упрощения примем, что механическая мощность не зависит от скольжения. Тогда, можно записать следующее соотношение:

Активная мощность как функция напряжения скольжения находится из схемы замещения следующим образом:

Рисунок 3

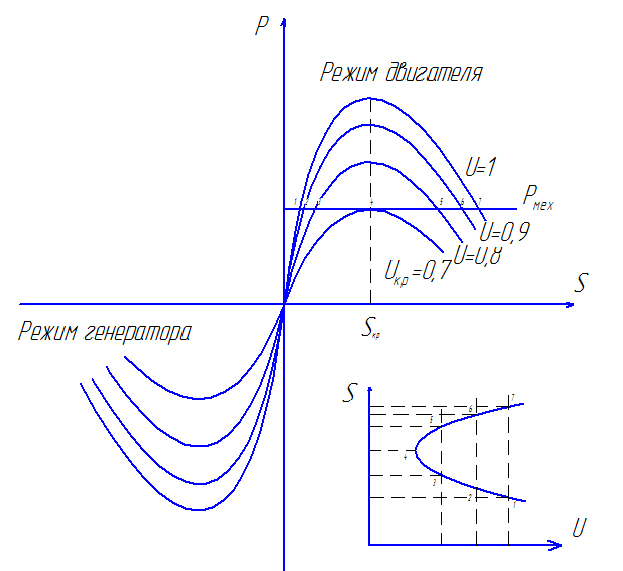
На рисунке 3 изображена зависимость между мощностью, напряжением и скольжением. При данной механической нагрузке Р_мех, у каждого двигателя есть определенный критический режим. Напряжение U_кр и скольжение S_кр, при котором этот режим наступает, называют критическими. Максимальный момент, который может развивать двигатель в критическом режиме, равен механическому моменту рабочей машины. При дальнейшем понижении напряжения работа невозможна, поскольку электрический момент оказывается меньше механического момента.

Значение максимального момента и критического скольжения можно определить, продифференцировав выражение мощности по скольжению и приравняв нулю:

.

“- ” – режим генератора;

“ +” – режим двигателя.

При этом скольжении находим значение максимальной мощности, т.е подставляем в формулу активной мощности и получаем:

.

Величина критического скольжения определяется через номинальное скольжение S₀ и кратность максимального момента b₀ :

;

.

Значение S₀ в основном зависит от мощности двигателя. Для малой мощности ( несколько кВт) она составляет 5 %, при средней мощности S₀ = 2% и у очень крупных двигателей ( сотни кВт) уменьшается до 1 %.

Используя понятия S_кр и P_max, перепишем выражения для мощности, которыми часто пользуются при расчетах электрических приводов:

.

Работа двигателя при положительном значении ( точки 1,2,3) устойчива, при отрицательном - неустойчива. Таким образом, у асинхронного двигателя имеется лишь одна область устойчивой работы между синхронной скоростью ( S=0) и критическим скольжением. Область между критическим скольжением и скольжением S=1, оказывается неустойчивой.

В нормальных условиях двигатель работает на устойчивой части своей характеристики, при значении S< S_KP. Однако, при снижении напряжения или увеличении механического вращающего момента, двигатель может оказаться в критическом режиме. При дальнейшем снижении напряжения, точка, характеризующая режим, перейдет на спадающую часть характеристики, двигатель тормозится, ток и реактивная мощность резко растут, а затем двигатель останавливается или опрокидывается. Обычно двигатели работают с большим запасом устойчивости. Их рабочее скольжение значительно меньше критического, а максимальный вращающий момент много больше рабочего ( 50-70%). В этих условиях, колебания напряжения не опасны с точки зрения устойчивости двигателей, и только очень большие снижения напряжения на их шинах (20-40%) приводят к опрокидыванию двигателей.

Лекция 9. Устойчивость узлов нагрузки

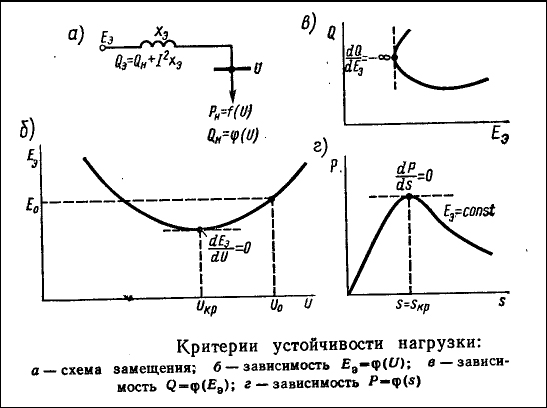
Смысл вторичного критерия устойчивости dE/dU=0 поясняется на вышеизложенных рисунках.

При снижении напряжения на шинах двигателя до величины 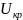отвечающей границе устойчивого режима, производная от экв. ЭДС по напряжению достигает нулевого значения. Т.о. нарушение устойчивости двигательной нагрузки характеризуется 3-мя соотношениями:

1. =0

2. =-∞

3. =0

Эти соотношения получаются из эквивалентной схемы замещения (рис.а), если напряжение на зажимах комплексной нагрузки рассматривать как величину зависящую от режима двигателя, а эквивалентную ЭДС рассматривать как независимую переменную. существует следующее соотношение:

U= =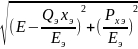

Если продифференцировать приведенное выражение по ЭДС, получим:

Из последнего соотношения следует, что при стремлении 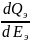к -∞, 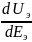стремится также к +∞, а обратная величина стремится к 0. Т.к условие 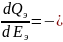∞ равноценно 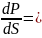0, то можно считать доказанной равноценность всех 3-х критерий.

ЛЕКЦИЯ №17

Мероприятия по улучшению устойчивости и качества

переходных процессов в электрических системах.

Изменение параметров и характеристик

элементов электрических систем.

1.Синхронные генераторы.

а) реактивное сопротивление СГ.

Статическая характеристика СГ - P =f ( ) = E ^. U sin ^.У₁₂ , отсюда :

P_max = (E_q^.U)/(Х_d+Х_c) – на улучшение статической устойчивости положительно влияет уменьшение значения сопротивления генератора Х_d. Изготавливаются специальные генераторы с «улучшенными параметрами» (уменьшается Х_d почти в два раза), но это достигается (конструктивно) за счет увеличения расхода материалов, повышения веса и габаритов машины, а следовательно, и ее стоимости.

б) параметры системы возбуждения.

АРВ сильного действия, а также форсировка возбуждения, особенно при их высоком быстродействии улучшают динамическую устойчивость СГ .

в) влияние демпферных обмоток.

Сказывается, главным образом, при работе генератора в асинхронном режиме и при больших качаниях. Определяемый ими асинхронный момент улучшает динамическую устойчивость СГ. Переходный процесс при этом затухает быстрее (рис.1).

Точка, характеризующая движение ротора, будет перемещаться не по штриховой кривой a k e f , а по кривой a b e. Эта кривая проходит выше кривой Р1 при положительном скольжении (увеличение угла δ) и ниже – при отрицательном скольжении (уменьшение угла δ). Это приводит к уменьшению F_уск. от a c a₁ a до a b a₁ a и увеличение F_торм. от c e e₁ c до b e e₁ c).

2. Выключатели.

Быстрое отключение КЗ имеет очень важное значение для улучшения динамической устойчивости. Влияние это отражается на соотношении площадок ускорения и возможного торможения (рис. 2).

3.Линии электропередачи.

За счет изменения конструктивного исполнения можно уменьшить реактивное сопротивлении линии, что влияет на максимальную передаваемую или предельную мощность ЛЭП и, соответственно, статическую устойчивость системы. Чаще всего это делают путем расщепления проводов. Уменьшение реактивного сопротивления линии передачи можно добиться также путем включения последовательно в линию конденсаторов (продольная компенсация), тогда : X_э= x₀L - Х_c.

Дополнительные мероприятия по улучшению

устойчивости электрических систем.

1. Заземление нейтралей трансформаторов.

Если вместо глухого заземления нейтралей трансформаторов (что применяется при U 110 кВ) использовать заземление нейтрали через небольшое, соответствующим образом подобранное, активное сопротивление, то величина напряжения в нормальном режиме изменяются мало, устойчивость же генераторов системы при двух- и, особенно однофазных КЗ увеличится из-за сравнительно меньшего сброса электромагнитной мощности генератора (рис. 3).

2. Электрическое торможение генераторов во время аварии.

При этом со стороны нейтрали генераторов или трансформаторов включаются активные сопротивления (рис..4). В нормальном режиме они закорочены выключателями В1. При КЗ эти выключатели отключаются и активные сопротивления оказываются включенными в цепь генератора.

Еще более эффективным является включение активных сопротивлений выключателем В2 параллельно генераторам или трансформаторам передающих станций. В этом случае действие нагрузочных сопротивлений продолжается и после отключения КЗ. Действие дополнительного нагревания сопротивлений объясняется поглощением в них избыточной мощности, развиваемой первичным двигателем и, соответственно, уменьшением сброса мощности.

3.Регулирование первичного двигателя.

Если оно осуществляется достаточно быстро, может снизить М_мех вслед за уменьшением М_{эл.магн.} и дать существенное улучшение динамической устойчивости (рис. 5).

Без регулирования: F_уск ( a b c a) > F_торм (c k м с) – режим динамически не устойчив.

При регулировании мощности турбины:

F_уск ( a b c’ o a) < F _{возм.торм} (c’ c k м f d c’) – режим устойчив.

Министерство образования РФ

Казанский Государственный Энергетический Университет

Кафедра электроэнергетические

системы и сети