
- •Лекция 1
- •Автономная электроэнергетическая система. Простейшая модель автономной электроэнергетической системы, представленная следующей схемой.
- •Лекция 2
- •Собственные проводимости
- •Лекция 3. Cтатическая устойчивость электрических систем
- •Лек 4. Динам устойчивость
- •6. Понятие динамической устойчивости электрической системы
- •Лекция 5 Оценка устойчивости перехода от одного режима к другому.
- •Лекция 6 Энергетические соотношения, характеризующие движения ротора генератора. Способ площадей и критерий устойчивости.
- •Определение предельного угла отключения короткого замыкания
- •Лекция №8. Метод последовательных интервалов.
- •Методическое пособие расчёт устойчивости электрических систем по дисциплине «Переходные процессы в электрических системах»
- •Часть 2.
- •1 Расчёт установившегося режима
- •2.Определение взаимных и собственных проводимостей при различных системах возбуждения
- •3. Определение коэффициента запаса статической устойчивости.
- •3.1 По действительному пределу передаваемой мощности, когда генератор эс не имеет арв
- •3.2 По действительному пределу передаваемой мощности , когда генератор эс имеет арв пропорционального действия
- •3.3 По действительному пределу передаваемой мощности, когда генератор эс имеет арв сильного действия
- •4. Расчёт динамической устойчивости системы
- •4.1 Расчёт предельного времени отключения линии при двухфазном к.З. При условии
- •5. Определение предельного времени отключения методом последовательных интервалов
- •Определение проводимостей методом единичных токов.
- •Метод эквивалентирования
- •Библиографический список
Лекция 5 Оценка устойчивости перехода от одного режима к другому.
Ранее были рассмотрены условия устойчивости системы подвергающиеся в установившемся режиме случайным малым возмущениям. При больших возмущениях (резких изменениях режима таких как короткое замыкание, отключение или включение каких-либо элементов системы: генератор, трансформатор, нагрузка, ЛЭП и т.д.), рассматривают задачу динамической устойчивости. Резкое изменение режима системы ( переход из режима 1 в режим 2) ведет к изменению электромагнитного момента на валу генератора системы.
Эффективный электромагнитный момент действует либо со стороны ротора, либо со стороны статора.
Появившейся
небаланс между ускоряющимся моментом
турбины и тормозящим электромагнитным
моментом генератора ∆ ,
приводит к тому, что генератор начинает
менять свою скорость. Если
,
приводит к тому, что генератор начинает
менять свою скорость. Если
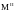 <
<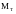 ,
то скорость будет увеличиваться сверх
синхронной на величину ∆
,
то скорость будет увеличиваться сверх
синхронной на величину ∆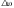 .
Избыточный момент ∆
.
Избыточный момент ∆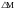 при этом будет уравновешиваться не
только электромагнитным моментом
отдаваемой в сеть электроэнергии
(тормозящий момент), но и моментом
отвечающим за накапливание ротором
кинетической энергией. Тогда уравнение
генератора записывается в следующем
виде:
при этом будет уравновешиваться не
только электромагнитным моментом
отдаваемой в сеть электроэнергии
(тормозящий момент), но и моментом
отвечающим за накапливание ротором
кинетической энергией. Тогда уравнение
генератора записывается в следующем
виде:
∆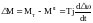 ,
,
где
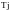 -
постоянная энерции якоря, момент
является
функцией скорости и изменяется при
изменении режима системы.
-
постоянная энерции якоря, момент
является
функцией скорости и изменяется при
изменении режима системы.
Интегрируя
полученное уравнение можно определить
изменение скорости ∆
.
Учитывая что
можно найти
= как функцию от времени.
как функцию от времени.
Изменение
скорости ∆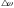 и угла
и угла
 позволяет судить
о том, сохранит ли система синхронную
работу (будет ли динамически устойчива)
после резкого возмущения и последующем
переходе от одного режима к другому.
Интегрирование уравнения движения или
аналогичного ему представляет значительные
трудности. В большинстве случаев его
удается провести, только применяя
приближенные методы. В некоторых случаях
динамическую устойчивость системы
можно проверить (грубо) без выявления
характера движения во времени по
соотношению возможных изменений энергии
в разных фазах движения. Этот
способ называется способом площадей.
позволяет судить
о том, сохранит ли система синхронную
работу (будет ли динамически устойчива)
после резкого возмущения и последующем
переходе от одного режима к другому.
Интегрирование уравнения движения или
аналогичного ему представляет значительные
трудности. В большинстве случаев его
удается провести, только применяя
приближенные методы. В некоторых случаях
динамическую устойчивость системы
можно проверить (грубо) без выявления
характера движения во времени по
соотношению возможных изменений энергии
в разных фазах движения. Этот
способ называется способом площадей.
При изменении параметров системы, на которую работает генератор, вследствие аварии (например, отключение одной из цепей ЛЭП, рис.9). изменяется электромагнитный момент и электрическая мощность, отдаваемая генератором. Пример такого изменения показан на рис. 10, где I-характеристика исходного (нормального) режима, а II-характеристика после отключения одной цепи.
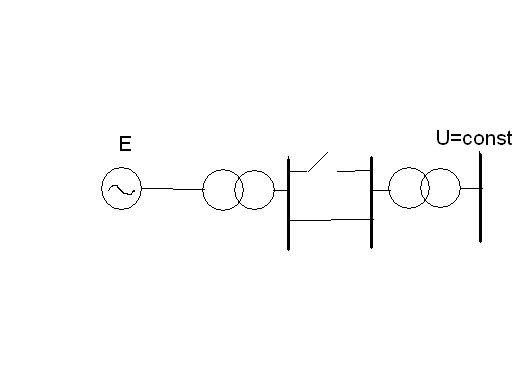
Рис.9 Схема аварийной системы
Изменение передаваемой мощности P=f() c кривой I на кривую II приводит к появлению небаланса мощности ΔP. Под действием этого небаланса происходит ускорение ротора генератора.
Способ площадей основан на сопоставлении площади S фигуры A,B,C и C,D,E. Если S (ABC) < S (CDE), то динамическая устойчивость при переходе от одного режима к другому охраняется, в противном случае отсутствует.

 D
I
D
I
А С E
II
В
0° 90° 180° δ
Рис.10
