Контрольные вопросы
1. Перечислите задачи, решаемые САП.
2. Приведите примеры входного, промежуточного и выходного языка САП.
3. Назначение препроцессора, процессора, постпроцессора.
4. Дайте классификацию имеющихся САП.
5. Какой промежуточный язык используется в САП перед постпроцессором.
6. Дайте сравнительные характеристики систем CAD/CAM.
9. Интерполяция. Аппаратные стойки чпу
Вопросы выполнения интерполяции хорошо изложены в литературе:
1. ПУ станками / под ред. В.Л. Сосонкина. – 1981. – С. 197–249.
2. СПУ ПУ и РТК / Б.Г. Коровин [и др.]. – 1990. – С. 158–172.
3. СПУ ПУ и РТК / О.П. Ильин [и др.]. – 1988. – С. 140–166.
4. Козырев В.М. Фазовые системы ЧПУ станками. – М.: Машиностроение, 1977.
Интерполяция – переделываю, подновляю, восстанавливаю (формообразование, т.е. согласованное движение по осям).
9.1. Траектории движения
1. Позиционирование с одновременным движением по 1-й оси (рис. 9.1):
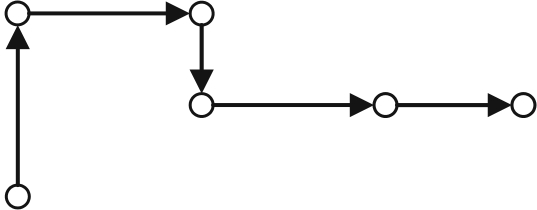
Рис. 9.1. Траектории движения позиционных роботов
2. Позиционирование с одновременным движением по двум и более осям (рис. 9.2):
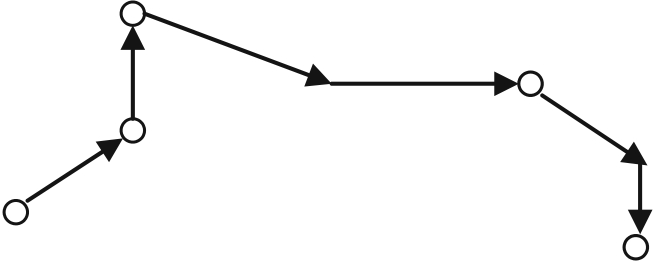
Рис. 9.2. Позиционирование для современных станков и роботов
3. Контурная линейная (рис. 9.3):
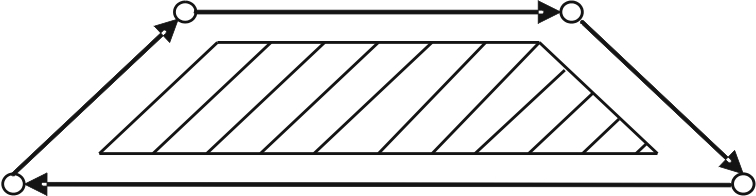
Рис. 9.3. Движение по эквидистанте при линейной интерполяции
4. Контурная круговая (рис. 9.4).
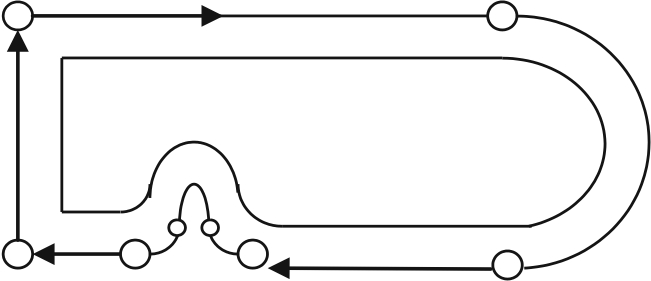
Рис. 9.4. Движение по эквидистанте при кривой интерполяции
9.2. Основные задачи при интерполяции
Интерполяция нужна только при контурной траектории движения. При интерполяции существуют две основные задачи:
1. Расчет опорных точек эквидистанты (траектории центра инструмента) по координатам опорных точек контура детали и по размерам инструмента, формирование заданий по координатным перемещениям.
2. Задание скорости во времени по осям, при обеспечении реализации заданной в УП траектории обработки детали:
задание контурной скорости
от кадра к кадру;
вычисление задания скорости по осям в функции времени в зависимости от заданного перемещения по осям, контурной скорости
,
т.е. формирование заданий в дискретной
форме
,
,
.
9.3. Математическое решение уравнений движения
Уравнение
прямой:
,
где
,
где
,
–
приращения по координатам.
Уравнение окружности:
,
где
,
–
координаты центра окружности.
В
производных уравнениях прямой и
окружности:
,
.
В параметрической форме уравнения прямой и окружности:
,
,
,
где
–
время обработки кадра при
,
,
–
угловая скорость движения по окружности.
Решения уравнений прямой и окружности заключается в применении двух интеграторов (рис. 9.5).
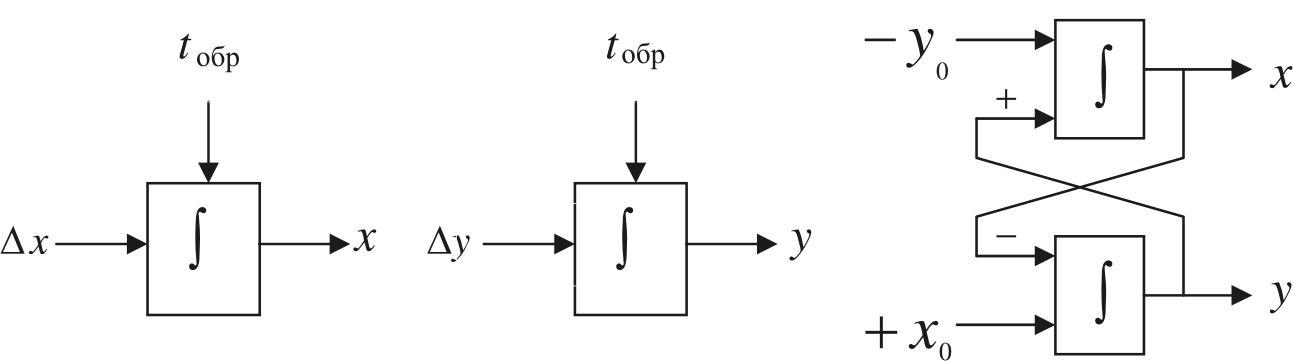
Рис. 9.5. Интегрирование при линейной и круговой интерполяции
Для линейной интерполяции
,
9.4. Реализация интегрирования в счпу
Интеграторы в СЧПУ всегда работают в дискретном виде, используя импульсную последовательность (унитарный код) или цифровой код. Это связано с требованиями точности, так как именно интеграторы обеспечивают необходимую точность формообразования детали.
При выполнении интеграторов в аппаратном виде (аппаратное моделирование) используются преобразователи кода в частоту. При этом выход интегратора – унитарный код (последовательность импульсов, общее количество которых задает перемещение, частота поступления – скорость по оси). Квант перемещения здесь постоянен – один импульс частоты, т.е. для линейной интерполяции x = y = ,
,
.
Временной интервал
между импульсами переменен и зависит
от осевой скорости
,
,
.
Это и является одним из недостатков
данного способа интегрирования, когда
максимальная частота выдачи импульсов,
а значит, и максимальная скорость
перемещения ограничены возможностью
СЧПУ (обычно
м/с).
При выполнении интеграторов программным путем на ЭВМ происходит прямое решение дифференциальных уравнений (обычно простейшим способом – методом Эйлера). Квант по времени постоянен и зависит от возможностей ЭВМ и от полосы пропускания непрерывной части. Величина приращения по координате за квант по времени зависит от максимально возможных скорости перемещения и ускорения на данном станке с данными приводами.
Уравнения интегрирования по i-й координате на j+1 шаге:
,
,
где
.
Для линейной интерполяции при Vk = const
,
.
При этом операции умножения заменяются операциями сложения и сдвига (деления пополам). На рис. 9.6, 9.7 приведены графики, демонстрирующие выходной код на приводы после интерполяции: круговой или линейной, при постоянном кванте перемещений (унитарный код) или постоянном кванте времени (цифровой код, где ±1ЕМР – вес единицы младшего разряда).
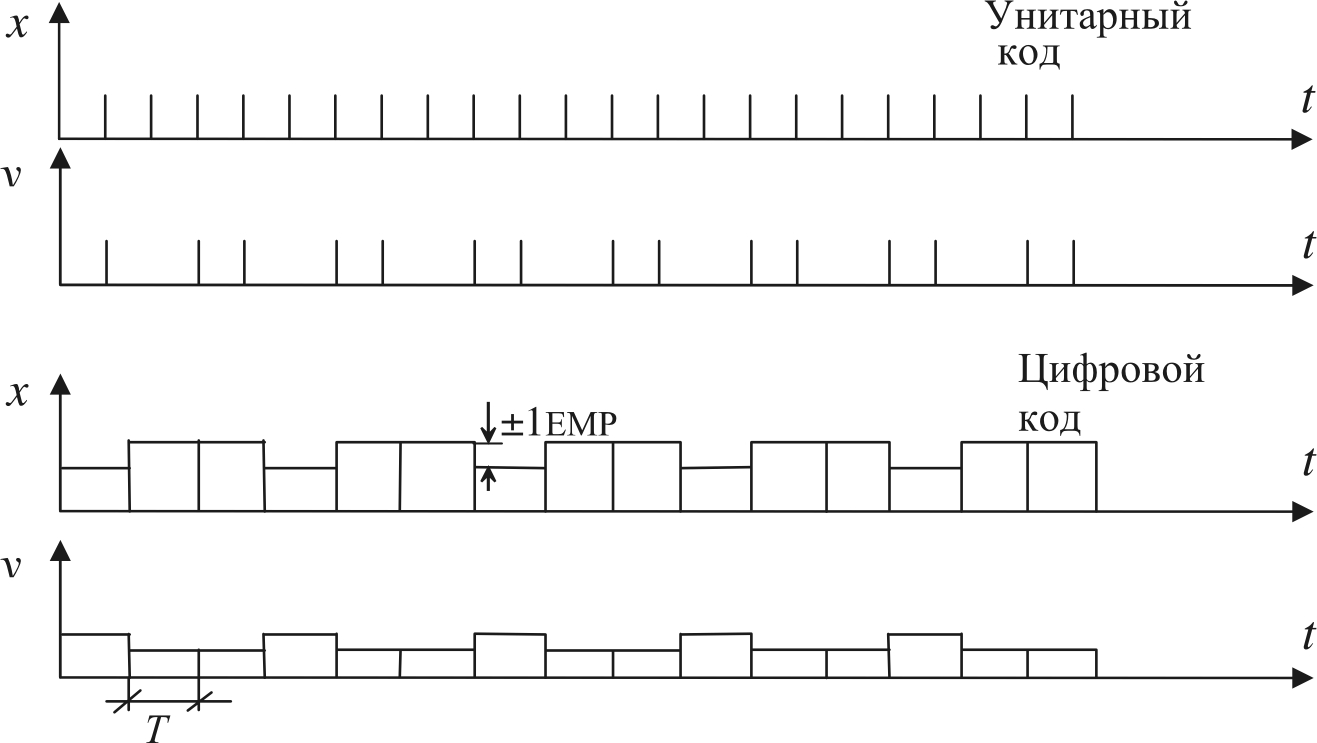
Рис. 9.6. Характер выходных сигналов интерполятора при линейной интерполяции для аппаратных и микропроцессорных СЧПУ
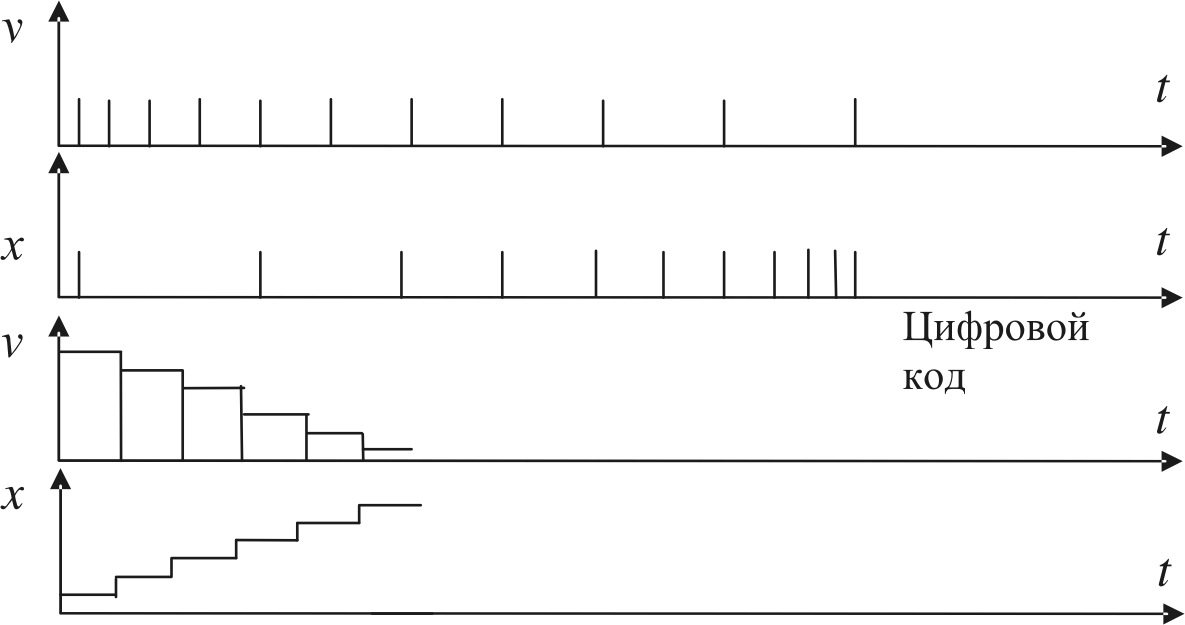
Рис. 9.7. Характер выходных сигналов интерполятора при круговой интерполяции для аппаратных и микропроцессорных СЧПУ
Конкретные системы УЧПУ с аппаратной реализацией интерполятора рассмотрены ниже.