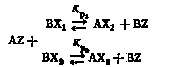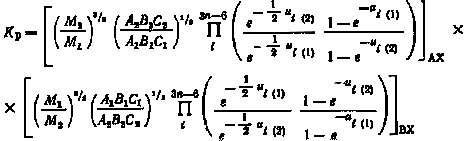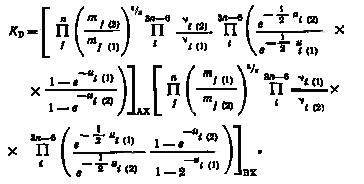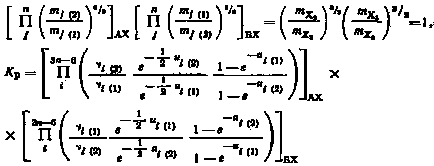Термодинамическое поведение изотопных частиц

Термодинамическое поведение изотопных частиц можно охарактеризовать константами равновесия однотипных реакций, происходящих с их участием.

Рассмотрим реакцию изотопных частиц BX₁ и ВХ₂ с веществом AZ, происходящую в конкурентных условиях при постоянных давлении и температуре:

(I)

Константы равновесия этих реакций выражаются соотношениями:

(II)

Используя в качестве меры идентичности термодинамического поведения изотопных частиц отношение констант равновесия реакций (I) и (II), получим:

     

     Ясно, что К_р—константа равновесия реакции

(III)

Эта реакция является реакцией изотопного обмена (см. гл. 2) и состоит в перераспределении изотопов X₁ и X₂ между молекулами АХ и ВХ. Таким образом, для определения степени идентичности термодинамического поведения двух изотопных частиц BX₁ и ВХ₂ в реакции с третьим веществом AZ нет необходимости рассматривать каждую из этих реакций. Достаточно знать К_р реакции изотопного обмена между веществами AX₁ и ВХ₂.

     Критерием идентичности термодинамического поведения изотопных частиц является равенство единице константы равновесия реакции (III).

     Константу равновесия этой реакции можно определять как экспериментально, так и расчетным путем. Расчет К_р основан на использовании фундаментальных соотношений химической и статистической термодинамики:

где G —изменение стандартного изобарно-изотермического потенциала (свободной энергии Гиббса) реакции (III); Q—полная статистическая сумма по состояниям молекулы; G — определяется выражением

     G =  (n_iG_i)_кон -  (n_iG_i)_нач

где n_i—число молей i-го компонента, участвующих в реакции. В нашем случае

G = GAX2 + GBX1 + GAX1 + GBX2.

(2.3)

Значение Q в выражении (2.2) определяется соотношением

     

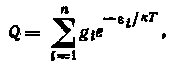
где _i — энергия 1-го квантового уровня молекулы; к — постоянная Больцмана; g_i—статистический вес i-ro энергетического уровня.

     Суммирование распространяется на все возможные энергетические уровни.

     На основании соотношений (2.1)—(2.3) для рассматриваемой системы

(2.4)

     Полные статистические суммы включают в себя их частные значения, связанные с различными видами движения. В общем случае отдельные виды движения в молекуле взаимосвязаны, однако с определенной степенью приближения их можно трактовать как независимые. Тогда сумма по состояниям молекулы может быть представлена в виде произведения частных статистических сумм:

     Q = g_ie^-_i^/kT = Q_постQ_врQ_колебQ_элQ_яд

где Q_пост—статистическая сумма, связанная с поступательным движением:

     

где М — молекулярная масса; —постоянная Планка; V—объем системы; Q_вр—вращательная статистическая сумма:

     

где А, В, С—главные моменты инерции частицы; S—число симметрии; Q_колеб — статистическая сумма, связанная с колебательным движением:

     

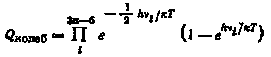
где n—число атомов в молекуле; _i—частота колебания для i-го уровня; Q_эл и Q_яд—статистические суммы, связанные с электронным и ядерным движением.

     Как видно из соотношения (2.4), константа равновесия K_p, характеризующая термодинамическое поведение изотопных молекул, определяется частным отношений полных статистических сумм однотипных изотопных молекул (АХ₂ и AX₁) и (ВХ₂ и BX₁). Для таких молекул электронные статистические суммы, числа симметрии, а также множители колебательных статистических сумм (за исключением множителей, относящихся к связям с изотопными атомами X₁ и X₂) одинаковы. Что касается множителей, относящихся к ядерным статистическим суммам, то они сокращаются в выражении для К_р, так как

      Q_яд(AX₁)=Q_яд(BX₁) и Q_яд(BX₂)=Q_яд(AX₂).

Подставляя значения полных статистических сумм в выражение (2.4) для константы равновесия К_р, получим

(2.5)

где u_i=hv_il(кТ). Это соотношение можно назвать первичным уравнением, определяющим термодинамическое поведение изотопных молекул. Наиболее трудно определить члены этого уравнения, связанные с вращательными статистическими суммами. Однако для изотопных молекул они могут быть исключены. Действительно, для изотопных молекул справедлива теорема Теллера—Редлиха:

(2.6)

где M₁ и М₂ — молекулярные массы изотопных частиц AX₁ и АХ₂, содержащих различные изотопные атомы; A, В, С—моменты инерции изотопных частиц AX₁ и AX₂; m_j(1) и m_j(2)—массы атомов, входящих в состав изотопных частиц; _i(1) и _i(2) —частоты колебаний атомов в изотопных частицах AX₁ и АХ₂.

     Подставляя выражение (2.6) в (2.5) получим

(2.7)

     Учитывая, что массы всех атомов, зa исключением в изотопных частицах совпадают, имеем:

     

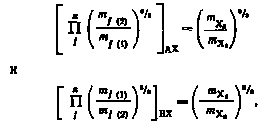
следовательно

(2.8)

     Поскольку замена одного изотопа другим в молекулах АХ и ВХ практически не сказывается на частотах колебаний всех связей, за исключением связей А—Х и В—X, то выражение (2.8) примет вид

(2.9)

В выражении (2.9) произведение

     

можно представить в виде

e -(1/kT){(1/2 h2,AX + 1/2 h1,BX) - (1/2 h1,AX + 1/2 h2,BX)}.

(2.10)

При этом множитель, заключенный в фигурные скобки, является разностью нулевых колебательных энергий конечных и начальных продуктов реакции (III) (рис. 1).

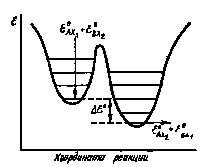Рис. 1. Изменение нулевой колебательной энергии для реакции (III)

     Как известно, колебательная энергия, отвечающая данному значению колебательного квантового числа, определяется выражением

      = (1/2 + v)k,

где v—колебательное квантовое число;  - основная частота, соответствующая переходу с нулевого колебательного уровня на уровень, отвечающий колебательному квантовому числу, равному 1. При  = 0 в соответствует нулевой колебательной энергии (⁰) и равно 1/2 hv.

     Таким образом, выражение (2.10) можно переписать следующим образом:

      e ^{-(1/kT){(0}_AX2 ^{- 0}_BX1) ^{- (0}_AX1 ^{- 0}_BX2^)} = e ^-(1/kT)(0_кон - ^0_нач) = е ^-0/kT,

где ⁰ — разность нулевых колебательных энергий конечных и начальных продуктов, реакции (III). Умножая числитель и знаменатель показателя степени на число Авогадро, имеем:

e-0/kT = e -0/RT,

(2.11)

где E⁰ — разность нулевых колебательных энергий, отнесенных к молярным количествам конечных и исходных веществ. Подставляя (2.11) в (2.9), получим

(2.12)

     Таким образом, для расчета констант равновесия реакций с участием различных изотопных частиц достаточно знать лишь частоты колебаний связей А—X₁, А—Х₂ и В—X₁, В—Х₂.

     Рассчитанные по уравнению (2.12) значения констант равновесия К_р (Т = 298 К) некоторых реакций изотопного обмена приведены ниже:

	Kp
AX1 + BX2 AX2 + BX1
HOH + HT HOT + HH	6,19
HOH + HD HOD + HH	3,18
13CO2 + 12CO32- 12CO2 + 13CO32-	1,016
79Br81Br + 79BrO-3 79Br2 + 81BrO-3	1,007
127I129I + 127IO-3 127I2 + 129IO-3	1,002
238UF6 + 235UF4 235UF6 + 238UF4	1,0001

     Как видно, значения констант равновесия существенно отличаются от единицы лишь для изотопов водорода. Для углерода и более тяжелых элементов значения К_р практически равны 1.