1.3.3 Сандар теориясы

1. Қалдықтар арифметикасы. Қалдықтар арифметикасы қарапайым арифметикаға ұқсас: ол коммутативті, ассоциативті, дистрибутивті. Бұған қоса n бойынша аралық келтірулердің нәтижесі секілді барлық есептеулердің қорытындысын n бойынша келтіру де сол нәтижеге ие болады.

(a + b) modn=((a modn) + (b modn)) modn

(a - b) modn=((a modn) - (b modn)) modn

(a ∙ b) modn=((a modn) ∙ (b modn)) modn

(a ∙ (b + c)) modn=((a∙b modn) + (a∙c modn)) modn

modn есептеуі криптографияда көптеп қолданылады, себебі дискретті логарифмдерді және квадраттық түбірлердің modn есептеуі оңай мәселе емес. Сонымен қатар, кеміту арифметикасы компьютерде оңай іске асырылады, себебі ол аралық мәндер мен нәтижелердің диапазонын шектейді. К биттердің кез-келген көбейту, алу және қосудың аралық мәндерінің нәтижелерін n бойынша кеміту 2k биттен аспайды [2]. Сондықтан кеміту арифметикасында біз үлкен аралық нәтижелерсіз дәрежеге шығарамыз.

n модулі бойынша дәрежеге шығарудың кері опреациясы дискретті логарифм.

2) Жай сандар. Жай сан деп тек бірге және өзіне бөлінетін санды айтамыз. 73, 2521, 2365347734339 және 2^756839-1 - жай сандар. Шексіз көп жа й сандар бар. Криптография, әсіресе ашық кілтті криптография көбінесе жай сандарды қолданады.

3) Екі сан өзара жай сан деп аталады, егер бірден басқа ортақ көбейткіштері болмаса. Басқаша айтқанда, егер a және n-нің ең үлкен ортақ бөлгіштері бірге тең. Ол былай жазылады:

ЕҮОБ( a, n)=1

Екі санның ең үлкен ортақ бөлгішін табудың әдісі – Евклид алгоритмі.

4) Модуль бойынша кері сандар. 4 санына кері сан 1/4. Ал кеміту арифметикасында жағдай қиындай түседі:

4∙x = 1 (mod7)

Бұл теңдеудің х және к-ті табу теңдеуіне эквивалентті:

4∙х = 7∙к + 1

мұндағы х және к – бүтін сандар. Есептің мақсаты х-ті табу:

1=(a∙x) modn

Оны былай да жазуға болады:

a^-1 ≡ x (modn)

Модуль бойынша кері санды мәселесі оңай емес. Кейде оның шешімі болады, кейде болмайды. Мысалы, модулі 14 болатын 5 санына кері сан 4. Ал модулі 14 болатын 2 санына кері сан жоқ.

Жалпы жағдайда a^-1≡ x(modn) теңдігінің шешімі болмайды. Егер a және n өзара жай сан болса, онда бірден n-1-ге дейінгі кез-келген сан n мен өзара жай сан болып, n-ге кері дәл бір сан болады.

5) Кіші Ферма теоремасы. Егер n жай сан болса, және a саны n-ге қысқармайтын болса, онда

a^n-1 = 1 modn

6) Эйлер теоремасы. Барлық a және n өзара жай сандар үшін

a^φ(n) ≡ 1 modn

мұндағы φ(n) – n-нен кіші және n-мен өзара жай сан болатын сандардың саны.

1.4 Криптографияның негізгі шифрлеу алгоритмдері

1. Симметриялық шифрлеу алгоритмі

1) Скремблер. Скремблер деп ақпараттың үздіксіз ағымының әр битін шифрлейтін алгоритмдердің программалық және аппараттық жүзеге асырылуын атайды [6]. Скремблердің өзі әр қадам сайын белгілі бір алгоритм бойынша өзгеріп отыратын биттердің жиынтығы болып табылады. Әр қадам орындалған сайын оның шығысында шифрлейтін бит (0 не 1) пайда болады, және ол бит XOR операциясы арқылы ақпараттық лектің ағымдағы битіне қойылады.

Соңғы уақытта скремблерлейтін алгоритмдердің қолдану аясы айтарлықтай азайған. Бұл бірінші кезекте берілген алгоритммен қауіпсіздігі қамтамасыз етілген ақпараттың әр битін тізбектеп тасымалдау көлемінің азаюымен түсіндіріледі. Қазіргі таңдағы жаппай барлық жүйелерде құпиялылығы блоктық шифрлермен қамтамасыз етілетін коммутациялық пакеттері бар желілер қолданылады. Ал олардың криптотұрақтылығы кейде скремблерлерден едәуір асып кетеді.

Скремблерлеудің мәнісі жүйеден өтетін мәліметтер легінің әр битін өзгертуден тұрады. Практикалық тұрғыда скремблерде жалғыз ғана XOR операциясы қолданылады. Скремблерден өтетін ақпараттың легімен қоса белгілі бір ережемен кодтайтын биттердің легі генерацияланады.

Кодтайтын биттердің тізбегін генерациялау аз ғана алғашқы ақпараттың, яғни кілттің көмегімен жүзеге асады. Ағымдағы ақпараттың жиынтығынан белгілі бір разрядтардың мәндері таңдалып, XOR операциясы арқылы өзара қосылады. Барлық разрядтар 1 битке жылжытылып, жаңа алынған мән босап қалған кіші разрядтың орнына орналастырылады. Жылжытуға дейінгі ең үлкен разрядтың орнында тұрған мән кодтайтын тізбекке қосылады.

Скремблер құрылғысы өте қарапайым. Оны электрондық және электрлік негізде жүзеге асыруға болады. Бұған қоса, шығыс тізбектің әр биті кірістегі бір ғана биттен тәуелді болуы лекпен тасымалданатын ақпараттың қауіпсіздігін қамтамасыз етуде скремблердің жағдайын жақсарта түсті. Бұл каналдарда міндетті түрде пайда болатын кедергілермен байланысты, себебі бұл жағдайда олар тек берілген биттерді, ал блоктық шифрлерде байттардың тобын бұрмалайды.

Скремблерделген тізбектерді дешифрлеу де дәл сол схема бойынша жүргізіледі. Ол үшін алгоритм дешифрлеу барысында қандай да бір қосымша есептеу шығындарынсыз-ақ қалпына келтірілетін XOR операциясы қолданады.

Скремблерлер негізінде шифрлеуде ең басты мәселе – жеткізетін және қабылдайтын құрылғылардың синхронизациясы. Бір биттің өзін ғана жоғалтып алғанда немесе қате енгізіп жібергенде бүкіл ақпарат кері қайтарылмайтындай жоғалады. Сондықтан скремблерлер негізінде шифрлеу жүйелерінде синхронизация әдістеріне көп көңіл бөлінеді. Тәжірибеде бұл мақсат үшін екі әдістің комбинациясы қолданылады:

Қабылдайтын жаққа алдын ала белгілі болатындай ақпарат легіне синхронизациялайтын биттерді қосу, қажетті бит табылмаған жағдайда жіберуші жақпен іздеу синхронизациясын бастайды.

Уақыттық импульстердің дәлдігі жоғары генераторларын пайдалану, бұл синхронизацияның жоғалу мезеттерінде қабылданып жатқан ақпараттың биттерін дешифрлеуде синхронизациясыз-ақ «жады бойынша» жүргізуге мүмкіндік береді.

Кері байланыспен қамтылған биттердің саны, яғни кодтайтын биттердің тізбегін шығаратын құрылғы жадысының разрядтылығы скремблердің разрядтылығы деп аталады. Сурет 1 көрсетілген скремблердің разрядтылығы 5-ке тең. Криптотұрақтылықтың параметрлеріне қарағанда бұл шама блоктық шифрлер кілттерінің ұзындығына сәйкес келеді. Скремблердің разрядтылығы өскен сайын оның криптотұрақтылығы да өсе түседі.

Скремблердің жеткілікті түрде көп жұмыс істеуі кезінде тұрып қалу байқалады. Белгілі такттардың санын орындаудан кейін скремблер ұяшықтарында бұрын кездескен биттердің комбинациясы пайда болып, және сол мезеттен бастап кодтайтын тізбек циклдік түрде белгілі бір периодпен қайталана беретін болады. Берілген мәселе өзінің табиғаты бойынша жойылмайтын болып табылады, себебі скремблердің N разрядында биттердің 2^N комбинациясы болуы мүмкін емес, демек 2^N-1 циклден кейін қайталану міндетті түрде болады.

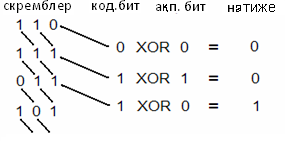
Сурет 1 - Скремблердің жұмыс істеу принціпі

«Барлығы нөл» комбинациясы скремблердің күйлерінің тізбегінен бірден алынып тасталынады – ол скремблерді дәл сол «барлығы нөл» күйіне алып келеді. Бұл «барлығы нөл» болатын кілт скремблер үшін лайықты емес екенін көрсетеді.

Жылжыту барысындағы генерацияланатын әр бит дәл сол кездегі скремблерде сақталып тұрған бірнеше биттен тәуелді. Сондықтан скремблерде кездескен қандай да бір жағдайдың қайталануынан кейін одан кейінгі барлық биттер скремблерде бұрын өткен тізбекті дәлме-дәл қайталайтын болады.

Осы жерде математика криптографияға кезектегі сыйлық сыйлады. Теореманың салдары бойынша кез-келген N разрядты скремблер үшін генерациялайтын биттер тізбегінің периоды 2^N-1 Бит болатындай әрқашан кері байланыспен қамтылатын разрядтарды таңдауға болады [6]. Мысалға, 8-биттік скремблердің 0-ші, 1-ші, 6-шы және 7-ші разрядтарын қамту барысында 255 Битті генерациялау кезінде тізбектен 1-ден 255-ке дейінгі сандар бірде-бір рет қайталанбай өтеді.

Берілген заң бойынша таңдалынған кері байланыстың схемалары ұзындығы ең үлкен тізбектердің генераторы деп аталады, және дәл солардың өзі скремблерлейтін аппараттарда қолданылады. Скремблерлердің электрлік немесе минималды электрондық негізде жасаған кездері ұзындығы ең үлкен тізбектердің генераторларының ішінен кезектегі битті құруға кететін разрядтардың саны минималды болатын скремблерлерді таңдаған [6]. Әдетте ең үлкен ұзындық тізбектерінің генераторлары 3 немесе 4 байланысқа дейін жеткен. Скремблердің разрядтылығы 30 биттен асып отырған, бұл 2⁴⁰ биттік ақпаратты қайталану қауіпінсіз тасымалдауға мүмкіндік береді.

Скремблер алгоритмдерінің елеулі кемшілігі – олардың фальсификацияға тұрақсыздығы.

2. Блоктық шифрлеу алгоритмі. Қазіргі таңда бірнеше криптографиялық берік блоктық шифрлер жасалып шығарылған. Практикалық тұрғыда алгоритмдердің барлығы дерлік өзгертулер үшін математикалық биективті (қайтарымды) қандай да бір жиынтығын қолданады.

Блоктық шифрлер ақпараттың блоктарын (4-тен 32 байтқа дейін) тұтас бір бүтін ретінде кодтайды – бұл толық қойып шығу шабуылдарына беріктікті едәуір көбейтеді және әр түрлі математикалық, алгоритмдік өзгертулерді қолдануға мүмкіндік береді.

Блоктық криптоалгоритмдердің өзіне тән ерекшелігі – олар өздерінің жұмысы барысында кіріс ақпараттың бекітілген ұзындығына өзгертулер жасап, дәл сол көлемдегі нәтижелік блокты алады да, бірақ кілті жоқ бөгде адамдардың оны оқуына мүмкіндік бермейді.

С=E(P, K)

(1)

P=D(C, K)

(2)

K кілті блоктық криптоалгоритмнің параметрі болып табылады және бекітілген өлшемдегі ақпарат түрінде беріледі. Берілген P және C мәліметтер блоктары өзара тең (кілтпен бірдей болуы міндетті емес) бекітілген разрядты болады.

Блоктық шифрлер тәжірибелік тұрғыда жүзеге асырылған барлық криптожүйенің негізі болып табылады [7]. Блоктық алгоритмдермен шифрленген байттардың тізбегін құру әдістемесі шексіз ұзындықтағы ақпараттың пакеттерін шифрлеуге мүмкіндік береді. Жұмыстың шапшаңдығы секілді блоктық алгоритмдердің мұндай қасиеті өздерінің табиғаты бойынша ақырын жұмыс істейтін асимметриялық алгоритмдерде де қолданылады. Блоктық шифрдің шығыс ағымындағы биттердің арасында статистикалық корреляцияның жоқтығы мәліметтер пакеттерінің бақылаушы сомасын есептеу үшін және параллельді хэштеу үшін қолданады.

Егер шифрленген мәліметтер блогын оқу үшін берілген хат мағыналы болғанша дейін тек мүмкін болатын барлық кілттерді қойып шығу арқылы мүмкін болса, криптоалгоритм идеалды деп аталады. Ықтималдық теориясы бойынша барлық кілттердің жартысын қойып шығудан кейін ізделініп отырылған кілт S ықтималдығы бойынша табылады десек, онда ұзындығы N болатын кілті бар идеалды берік алгоритмді бұзу үшін орта есеппен 2^N -1 тексерулер қажет. Сонда, жалпы жағдайда блоктық алгоритмдердің беріктігі кілттің ұзындығына тәуелді және оның артуына байланысты экспоненциалды түрде артады.

Бұдан басқа идеалды берік криптоалгоритмдерге тағы да бір өте маңызды талап қойылады. Берліген және шифрленген блоктары белгілі болған жағдайдың өзінде өзгерту жүргізілген кілт тек толық қойып шығу арқылы табылу қажет. Бөгде адамдарға берілген мәтіннің белгілі бір бөлігі белгілі болатын жағдайлар көптеп кездеседі. Бұл электронды бланктардың стандартты жазулары, файл форматтарының бекітілген тақырыбы, мәтінде едәуір жиі кездесетін ұзын сөздер және байттардың тізбегі. Сондықтан берік (1) блоктық шифрдің функциясына келесідей шектеулер қойлады:

1. E функциясына кері қайтарымды болуы тиіс;

2. Кілттерді толық қойып шығудан басқа P хатын белгілі C блогы бойынша оқудың басқа әдістері болмауы тиіс;

3. Кілттерді толық қойып шығудан басқа P хаты C хатына қай кілтпен өзгертілгенін анықтаудың басқа әдістері болмауы тиіс;

Кілттің материалы бірнеше рет тікелей және қосалқы қолданылуы блоктық алгоритмдердге тән сипат болып табылады. Бұл берілген және шифрленген мәтіндер белгілі болғанда кілтке қатысты кері декодтау жасау мүмкіндігінің жоқтығы талабына сәйкес келеді. Бұл мәселені шешу көбінесе кілттің не оның бір бөлігінің мәні емес, қандай да бір кері қайтарымсыз функция қолданылады. Бұған қоса мұндай өзгертулерде дәл сол блок не кілттің элементі бірнеше рет қолданылады.

Бұл P шамасына қатысты функциясының кері қайтарымды шартының орындалуы барысында K кілтіне қатысты функциясын кері қайтарымсыз ете алады. Жеке хатты кодтау барысында ақпараттың пакеттерін шифрлеу және дешифрлеу операциялары бірнеше рет орындалатын (кейде бірнеше мың рет) болғандықтан, ал кілттің мәні, яғни V_i(K) функциясы өзгеріссіз болғандықтан, онда кейде мәліметтердің мәндерін алдын ала есептеп, кілтпен бірге сақтап қою мақсатқа лайықтырақ келеді [7]. Бұл мәндердің барлығы тек кілтке тәуелді болғандықтан, оларды криптографияда кілттің материалы деп атайды. Берілген операция не кілттің ұзындығын, не алгоритмнің криптотұрақтылығын өзгерпейтінін атап өту қажет. Бұл жерде аралық нәтижелерді кэштеу арқасында есептеу жылдамдығын оптимизациялау жүреді.