2 Компьютерлік криптографиядағы детерминделген хаос жүйесін басқаруды іске асыру

2.1 Лоренцтің сызықсыз дифференциалдық теңдеулер жүйесін теориялық зерттеу

Лоренцтің сызықсыз дифференциалдық теңдеулер жүйесі:

(8)			(8)
мұндағы		x1, x2, x3 – диффренциалдық жүйенің айнымалылары,
		а, b, r – дифференциалдық жүйенің параметрлері

Лоренц теңдеулер жүйесі деп аталған бұл жүйе құрамында алғаш рет ретсіз аттрактор көрсетілген динамикалық жүйе болып табылады (σ = 10, b = 8/3, 24.06 < r < 28 болғанда Лоренц аттракторы байқалады) [17]. Лоренц жүйесі зерттелген монографиялар мен университеттік курстаға көптігіне қарамастан, Лоренц аттракторы не екеніне әлі толық ұғым қалыптаспаған.

Э. Лоренц (8) жүйені сандық интегралдау нәтижесінде σ = 10, b = 8/3 и r = 28 болғанда мынаны анықтаған: бір жағынан барлық траекториялардың хаостық, ретсіз қозғалыстары байқалса (Сурет 9-да траекториялардың x₂ координатасының уақыттан тәуелділігі көрсетілген), ал екінші жағынан, барлық траекториялар кезінде қандай да бір құрылымы күрделі аттрактор (ағыл. to attract - тарту) жиына жиналады.

Сурет 9

Шешімдердің мұндай іс-әрекетін сұйықтықтардың турбулентті (хаостық, бейберекетсіз) ағысына ұқсатады. Бұл қазіргі таңдағы гидро- және аэродинамиканың ең маңызды мәселелерінің бірі – турбуленттілікті сипаттау мәселесінде алға жылжуға үміт тудырды. Ғалымдардың бұл жүйеге қызығушылығы осымен түсіндіріледі. Қазіргі уақытта Лоренц жүйесі мен оның аналогтары турбуленттілікке қатысы бар ма деген сұраққа жауап белгісіз болып отыр. Бірақ мұнда қолдайтын да , теріске шығаратын да бірнеше дәлелдер бар.

Лоренц жүйесіндегі аттрактордың пайда болуын және оның құрылымын сипаттап көрейік. (8)-де σ = 10, b = 8/3 деп алып, r-ді нөлден бастап арттырамыз.

r<1 болғанда Лоренц жүйесінде координаталар басы болатын асимптотикалық орнықты стационар нүктесі болады. Оған барлық траекториялар тартылады (Сурет 10). r бірден асқанда жүйеде алғашқы бифуркация болады. Координаттар басы орнықтылығын жоғалтып, одан орнықты жаңа екі стационар нүкте бөлініп шығады:

X₁ = (√b(r – 1), √b(r – 1), r – 1)

X₂ = (–√b(r – 1), –√b(r – 1), r – 1

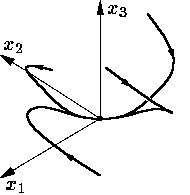
Сурет 10

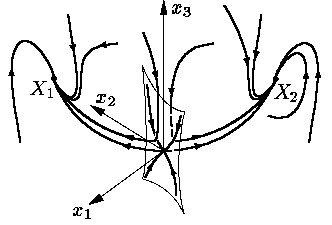
Нөлдік стационар нүктеде сызықты жүйенің екі теріс және бір оң дербес мәндері болады. Осыған сәйкес нөлдік стационар нүктенің екі кіріс мұртшасы және бір шығыс мұртшасы болады (Сурет 11). X₁ и X₂ нүктелерінде сызықты жүйенің барлық дербес мәндері теріс болады.

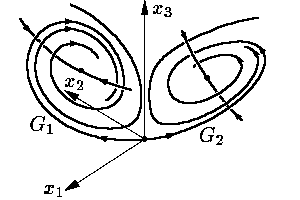
r параметрінің өсуі барысында жүйенің теріс дербес мәндер жұбы комплекстік түйіндес дербес мәндерге айналады. Бұл нөлдік стационар нүктеден шыққан G₁ мен G₂ мұртшалары X₁ мен X₂ стационар нүктелерінің маңайында спираль сияқты орала бастайды (Сурет 12).

Сурет 11	Сурет 12

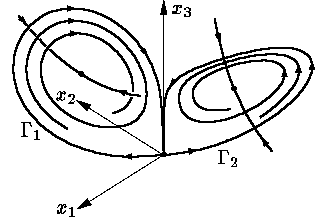
Бұдан арғы r-дің өсуінен кейін X₁ мен X₂ стационар нүктелер жоғары көтеріледі (олар x₃=r-1 жазықтығында жатыр), ал спираль түріндегі траекториялар “үлкейеді”. Бұл r ≈ 13.92 болғанда нөлдің шығыс мұртшалары ретінде басталатын спираль оның кіріс мұртшаларымен түйісіп, екі гомоклиникалық Γ₁ мен Γ₂ траекториясын түзеді (Сурет 13).

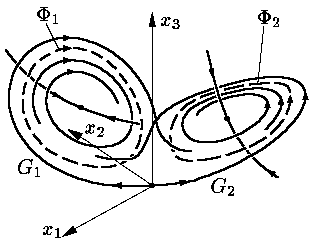
r-дің артуы барысында Φ₁ және Φ₂ орнықсыз циклдерін құратын гомоклиникалық траекториялардың бифуркациясы болады (Сурет 14). Бұл циклдарға жауап беретін ілесу операторларының сызықты бөлігінің бірден үлкен және бірден кіші бір-бірден мултипликаторлары бар, демек, бір бағыт бойынша траекториялар бұл циклдарға тартылады, ал екіншісінде алшақтайды.

Сурет 13	Сурет 14

Нөлдік стационар нүктеден шығатын G₁ мен G₂ мұртшалары енді оның кіріс мұртшаларымен түйіспейді, олар X₂ және X₁ стационар нүктелерінің тарту облысына кіреді, сәйкесінше (бұрынғыдай X₁ және X₂ емес) олардың маңайында орақталады.

r ≈ 24.06 болғанда тағы да бір бифуркация болады және G₁ мен G₂ Φ₁ және Φ₂ циклдарының тарту әр алуандығына (орнықсыз) түседі. Келесі бифуркация r = r₀ = σ(σ + b + 3)/(σ – b – 1) ≈ 24.74 кезінде болады. Бұл кезде X₁ және X₂ нүктелерінде сызықталған жүйенің жорамал осінің бойында дербес мәндер жұбы пайда болады (r>r₀ болғанда бұл дербес мәндердің оң нақты бөлігі болады). X₁ және X₂ нүктелері орнықтылығын жоғалта отырып Φ₁ және Φ₂ орнықсыз циклдерін жұтып алады (Пуанкаре-Андронов-Хопф бифурациясы). Жүйе қатты қоздырылады.

Сипатталған үрдіс барысында r ≈ 13.92 бастап Лоренц жүйесінде шекті инвариантты жиын пайда болады, бірақ r = r₀ дейін орнықсыз болады, яғни траекторияларды өзіне тартпайды . Λ жиыны r Є (r₀,50] кезінде орнықты бола бастайды. Бұл Лоренц аттракторы болып табылады. Сурет 15-де r=28 кезіндегі Лоренц аттракторының бір траекториясы бейнеленген: траектория біресе X₁ орнықсыз стационар нүктесінде, біресе X₂ орнықсыз стационар нүктесінде оларды кездейсоқ ауыстыра отырып бірнеше орам жасайды.

Лоренц аттракторы келесі қасиеттерге ие екені белгілі.

Біріншіден, Λ жиынын аттрактор дейміз, егер ( мұндағы g^t – Лоренц жүйесінің траекториялары бойынша жылжу операторы) болатындай R³-те ашық A жиыны бар болса. Басқаша айтсақ, А-дан басталатын ( бұл жағдайда А ретінде координаталар басынан басқа барлық R³-ті алуға болады) барлық траекториялар Λ-ге тартылса.

Екіншіден, Λ-де әрқайсысы орнықсыз болатын барлық жерде тығыз периодикалық траекториялардың жиыны болады.

Үшіншіден, Λ-де жатқан траекториялар экспоненциалды өседі, сондықтан алғашқы мәндерінің соншалықты аз қозуынан Лоренц жүйесі үшін Коши есебінің үлкен интервалдағы шешімдерінің айырмашылықтары тым көп болуы мүмкін. Бұл Лоренц жүйесіндегі үрдістің сипатын детерминделген етеді.

Төртіншіден, локальді түрде Лоренц аттракторының құрылымы жетілдірілген кантор жиынының кесіндіге көбейтіндісі ретінде болады.

Аталған қасиеттерге ие аттракторлар көптеген динамикалық жүйелерде табылған. Ол көбінесе оғаш аттрактор деп аталады.

r-дің үлкен мәндерінде Лоренц жүйесінде не болатыны әлі белгісіз болып отыр. Параметрледің кейбір өзгеру интервалдарында орнықты периодикалық шешімдер табылған. r Є[210, 234] және r Є [145, 149] болғанда қызық құбылыстар байқалады. r=234 болғанда Лоренц жүйесінің орнықты циклі болады, ал r азайған кезде қосарланған периодтың бифуркациясынан өтеді. r-дің ары қарай азаюында жаңа цикл де орнықтылығын жоғалтып, бұл цикл де, өз кезегінде, жаңа қос периодты цикл тудырады. Сонымен, Лоренц жүйесінің қос периодты бифуркациясына ұшырайтын параметр мәндерінің шексіз {r_k} тізбегі шығады. Бұл тізбек жақында жарыққа шыққан универсалды Фейгенбаум заңын қанағаттандырады:

(9)

мұндағы σ = 4.6692… - универсалды тұрақты, қазіргі уақыттағы пайымдау бойынша қос периодты бифуркациялардың шексіз тізбегінен өтетін нақты бір динамикалық жүйелерге тәуелді болмайды.

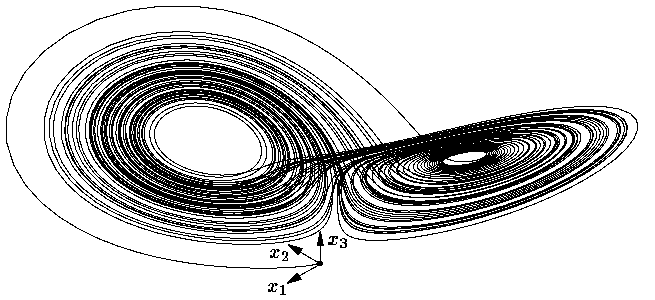
Сурет 15 – Лоренц аттракторы