1.2.2 Криптография мен хаостық динамиканың өзара байланысы

Біз криптографияның және хаостық динамиканың кейбір ұғымдарын қарастырдық. Дәстүрлі криптожүйелерді (шифрлеу сұлбаларын, псевдокездейсоқ генераторларды ) ақпаратты өзгертетін динамикалық жүйе ретінде қарастыруға болады (Кесте 2).

Хаостық жүйенің жүйедегі тәуелсіз айнымалыларының санынан аз бөлшектік өлшемділігі бар болуы мүмкін (Сурет 3 сол жағынан). Криптографиялық жүйелерде өлшемділігі максималды әрі толық болатын кеңістікті қолдануға тырысады (Сурет 3 оң жағынан).

Кесте 2- Хаос теориясы мен криптографияның зерттеу нысандарының арасындағы өзара байланыс

Хаос теориясы	Криптография
Хаостық жүйе	Псевдокездейсоқ жүйе
- сызықсыз өзгерту	- сызықсыз өзгерту
- күйлердің шексіз саны	- күйлердің шекті саны
- итерациялардың саны	- итерациялардың саны
алғашқы күй (алғашқы шарт)	ашық мәтін
қорытынды күй	шифрленген мәтін
алғашқы және қорытынды күйлердің асимтотикалық тәуелсіздігі	Шатыстыру
параметрге сезгіштік, араластыру	Тозаңдату

Сурет 3 - Хаостық және криптографиялық жүйелердің фазалық бейнелерінің мысалы

Хаостық жүйелердің белгілі қасиеттері (траекториялардың экспоненциалды таралуы, араластыру) криптографияға пайдасын тигізер деп есептеуге болады (шифрлеудің жаңа сұлбаларын құрастыруда).

Зерделеу нысаны мен қойылатын назар аударуларға көзқарас бойынша криптография мен хаос теориясы арасында фундаметальді айырмашылықтар бар:

1. Криптография итерациялық өзгертулердің шекті сандарының әсерін зерттесе (n<∞), хаос теориясы (үздіксіз және дискретті) жүйенің асимтотикалық әрекетін (n →∞) зерттейді.

2. Классикалық хаостық жүйелер көбінесе өлшемділігі бөлшектік болатын (яғни фракталдар) күй кеңістігіндегі қандай да бір нысанмен беріледі. Криптографияда біз тәуелсіз айнымалылардың мүмкін болатын барлық комбинацияларын қолдана отырып (бұл жүйені барынша болжамсыз етеді), өлшемділігі бүтін кеңістікпен жұмыс істейміз (Сурет 3).

3. Маңыздысы, компьютерлік криптографияда күйлерінің саны шекті болатын жүйелер қарастырылады, ал хаостық жүйенің күй кеңістігі үздіксіз және дискретті мәндердің шексіз жиынында анықталған. Сонымен, компьютерде орындалған хаостың барлық модельдері жақындатылған болып табылады.

Нысан бөгде адам (криптоаналитик) үшін абсолютті түрде болжамсыз болған жағдайда ғана оның идеалды қауіпсіздігі (perfect security) орын алады. Бұл мүмкін болатын барлық нәтижелердің (күйлер) ықтималдықтары бірдей және алдыңға күйінен тәуелсіз екенін білдіреді. Басқаша айтсақ, күйлер тізбегі ықтималдықтың біркелкі таралу заңымен сипатталады, және корреляциялары (паттерндер) болмайды. Абсолютті болжамсыздық ұғымы шынайы кездейсоқтық ұғымына эквивалентті (Сурет 4). Бұған қоса, шынайы кездейсоқ тізбек көбінесе ақ шу деп те аталады. Еркіндік дәрежесінің мөлшері үлкен болатын хаостық жүйе ақ шудың көзі бола алады (мысалға, идеалды газы бар тұйық жүйе).

Сурет 4- Шынайы кездейсоқтық, псевдкездейсоқтық, алгоритмдік кездейсоқтық және ұқсас ұғымдар сыныптары

Шынына келгенде, криптографиялық жүйелер идеалды қауіпсіздіктен едәуір төмен болатын практикалық қауіпсіздікті қамтамасыз етеді (эксплуатациялық және экономикалық мақсаттарға сәйкестілігіне байланысты). Кездейсоқтық және болжамсыздық ұғымдары сәйкесінше псевдокездейсоқтық және есептеу (полиноминалды) болжамсыздығына алмастырылады. Псевдокездейсоқтық нысанды шынайы кездейсоқ нысаннан сырт бақылаушының қол жететін есептеу құралдары арқылы айыру мүмкін емес. Осыған ұқсас, есептеу тұрғысынан болжамсыз нысанның әрекеті сырт бақылаушының есептеу құрылғыларымен божанылуы мүмкін емес. Псевдокездейсоқ нысан есептеу тұрғысынан болжамсыз екенін дәлелдеуге болады.

Әрине, шынайы кездейсоқ нысан алгоритмдік кездейсоқ және псевдокездейсоқ болады (Сурет 4). Бірақ, псевдокездейсоқтық және алгоритмдік кездейсоқтық ұғымдары бір-бірінен ажыратылады: псевдокездейсоқ қатар шағын генератормен құрылады, бірақ сырт бақылаушы бұл генераторды құра алмайды және тізбекті болжай алмайды.

Табиғи хаос (зат, табиғат, әлем) зор өлшемділікке ие сансыз көп күйлердің жиынына және «итерациялық функциялар жүйесінің» қамтыла алынбайтын күрделікке ие. Соған қарамастан, мұндай жүйелердің энтропиясы өз-өзінен құрылу есебінен сәйкес масштабтағы «мүлдем кездейсоқ» жүйелерге қарағанда едәуір аз болады. Көп өлшемді хаостық жүйелер қайта шығарылмайтын болғандықтан, олар шифрлеуде қолданыла алмайды. Екінші жағынан, «табиғи» хаостың көмегімен кілттерді генерациялау (қайталану мүмкіндігінсіз) қазірдің өзінде кеңінен қолданылады (мысалға, компьютердегі жүйелік блоктың терминалдық шуы).

Шифрлеу алгоритмінде қолданылайын деп отырылған детерминделген хаос аз ғана өлшемділікке және күйлердің сансыз көп жиынына ие. Сірә, бұл жүйелер табиғи хаосқа қарағанда болжауға «келіңкірейді», бірақ адамның қолымен модельге салынуы мүмкін. Мұндай жүйелерді бағалау үшін біз Колмогоров-Синай энтропиясын (Ляпунов көрсеткішімен және алгоримтдік күрделілікпен байланысты) қарастырамыз, және детерминделген хаос алгоритмдік кездейсоқ тізбектерді тудыра алатынын көреміз. Бұған қоса, араластырушы жүйеде x_n, x_n+k, x_n+2k, x_n+3k … іріктелуі асимтотикалық (к →∞) кездейсоқ болып табылады, яғни к үлкейген сайын мүшелердің іріктелу тәуелділігі азая береді.

1) Колмогоров-Синай энтропиясы. Ляпунов экспонентасының көрсеткіші уақыт өткен сайын жүйені болжау мүмкіндігін қалай тез жоғалтатынымызды көрсететін алғашқы мөлшерлік ақпарат береді. Мұндай мағынада, бұдан артығырақ пайдалы бағаны Колмогоров-Синайдың h_ks энтропиясы бере алады [14]. h_ks энтропиясы жүйені бақылауға рұқсат етуді (өлшеудің дәлдігі) ескереді.

β= {x₁, x₂, …,x_m } бөлінуі бақылаушының рұқсат ету мүмкіндігін көрсетеді. Ағымдағы x күйін өлшей отырып, бақылаушы тек x ∈ X_i, символ δ(X_i): x ∈ X_i фактісін ғана анықтай алады.

n-символды траекторияның a_n∈Aⁿ энтропиясы β бөлінуінде берілсін

мұндағы Pr(a_n) - a_n символды қатаршаның пайда болу ықтималдығы

(n+1)-ші символдың шартты энтропиясы (a_n траекториясынан кейінгісі белгілі болғанда) мынаған тең

β бөлінуінің энтропиясы

Колмогоров-Синай энропиясы мүмкін болатын барлық бөлінулер жиынының дәл жоғарғы h_β шекарасы

(7)

(7) h_ks энтропиясы регулярлы жүйелер үшін нөлге тең, детерминделген хаос үшін оң және шекті және кездейсоқ шамалар үшін шексіз. h_ks энтропиясы Ляпунов көрсеткіштерімен байланысты және хаостық жүйенің күйін болжауға болатын T уақыт интервалына пропорционал.

2) Псевдокездейсоқ генератор. Формальді емес тұрғыда, егер генератор кірісінде қысқа тізбекті (дән) алып, шығысында одан ұзын (әдетте өте ұзын тізбек) псевдокездейсоқ тізбекті алса, онда ол псевдокездейсоқ генератор тиімді деп аталады [14].

Анықтама (Псевдокездейсоқ генератор). функциясы барлық үшін l(n)>n шартын қанағаттандыратын болсын. l(n) ұзартатын функциясы бар псевдокездейсоқ генератор келесі қасиеттерге ие болатын полиноминалды G алгоритмі болып табылады:

1. Кез-келген үшін орынды

2. және 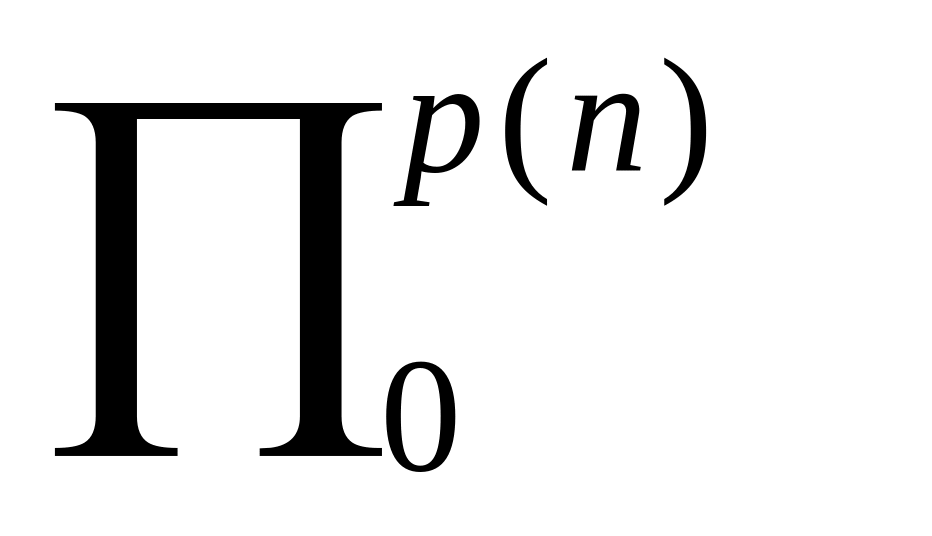ықтималдық ансамбльдері жеткілікті түрде үлкен n үшін есептеу тұрғысынан айыру мүмкін емес.

Теорема (псевдокездейсоқ генераторды құру). f – функциясы ұзындығын сақтайтын біржақты функция болсын, және b предикаты f-тің берік ядросы болсын. Онда G(α) теңдігі l ұзартатын функциясы бар псевдокездейсоқ генератор болып табылады.

Теорема (псевдокездейсоқ генератордың бар болуы). Псевдокездейсоқ генераторлар тек біржақты функциялар болғанда ғана бар болады.

Псевдокездейсоқ генератормен шоғырланатын тізбектің үлестіру тығыздығы, шынына келгенде, біркелкі болмауы мүмкін, бірақ ол есептеу тұрғысынан біркелкі тығыздықтан айырмашылығы болмауы мүмкін.

3) Псевдокездейсоқ генераторларды тексеру. Криптографияның классикалық мақсаты псевдокездейсоқ деп есептелетін генераторлардың сапасын бағалау. Псевдокездейсоқ генераторлардың берілген анықтамаларын практика тұрғысынан толық тексеру мүмкін емес. Сондықтан псевдокездейсоқ генератордың біркелкі үлестіруден ауытқуды анықтайтын псевдокездейсоқтыққа зерттеу экспериментальді түрде өтеді. АҚШ-тың Стандарттар мен Технологиялардың Ұлттық Институты 16 түрлі тестті ұсынады. Олардың ішіндегі ең мағыздыларына тоқталып өтейік:

Монобиттік тест. Тізбектегі бірлер мен нөлдердің саны шамамен бірдей болуы тиіс.

Жиіліктік тест. m-биттік блоктардың(көбінесе m=4) үлестіру тығыздығы шамамен бірдей болып көрінуі тиіс (x² үлестіру арқылы тексеріледі).

Жүрістер тесті. Жүріс деп тек нөлдерден және тек бірлерден (0, 1, 00, 11, 000, 111…) тұратын қатаршаны атаймыз. Онда жүрістердің ұзындықтары кездейсоқ тізбекке сәйкес келуі тиіс, яғни барлық жүрістердің жартысының ұзындығы 1 Бит, төрттен бір бөлігі 2 Бит, сегізден бір бөлігі 3 Бит және т.с.с..

1.2.3 Хаос және псевдохаос

Алдыңғы бөлімде біз хаостық жүйе базасының негізінде құрылған псевдокездейсоқ генератордың моделін қарастырып, оның алгоритмдік кездейсоқ шексіз тізбектерді тудыра алатынын көрдік. Бұған қоса, бұл тізбектерді іріктеу асимтотикалық кездейсоқ болуы мүмкін. Дегенмен, бұған дейін күйлерінің саны шексіз болатын хаостық жүйелер туралы ғана сөз қозғалған.

Хаостық жүйе күйлерінің саны шекті болатын машинада іске асырылмайтынын түсіну оңай. Жүйенің әр кейінгі күйі одан алдыңғы қандай да бір күйдің траекториясымен сәйкес келмеуі мүмкін [16]. Кері жағдайда траектория циклдік орбитаға айналады. Хаостың барлық компьютерлік модельдері математикалық хаостың аппроксимациясы (жақындатылуы) болып табылады. Алғашқы итерацияларда аппроксимация белгілі бір деңгейде берілген жүйенің қасиеттерін береді, бірақ n→∞ шегінде асимтотикалық қате жақындатуға әкеледі (яғни модельдің траекториясы мен берілген жүйенің траекториясы ажырап кетеді). Компьютерлік аппроксимацияларды псевдохаос деп атайтын боламыз.

Псевдохаостық жүйенің әрекеті берілген хаостық жүйеден сапалы түрде айырықшалануы мүмкін. Демек, хаостық жүйенің болжамсыздық қасиетін оның аппроксимациясына бірден көшірген дұрыс емес (Сурет 5).

Бұл сұраққа хаостық жүйелер секілді универсалды жауап әзірше жоқ.

Бүгінгі таңда, псевдокездейсоқ генераторлар тесттердің көмегімен сынақтан өткізіледі.

Псевдохаостық криптожүйелер құруда циклдік орбитаның минималды және орташа ұзындығын білу маңызды [14]. Криптожүйелердің әр түрлі класстары орбитаның ұзындығына әр түрлі талаптар қояды:

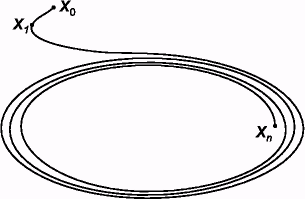
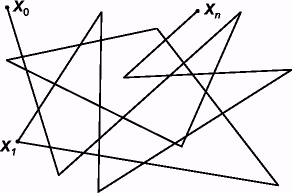
• Ұзындықтары қысқа орбиталар өте қауіпті, себебі олар паттерндердің құрылуына әкеледі (Сурет 6(а)).

• Ұзын тізбекті лектік шифрлер мен псевдокездейсоқ генераторлар үшін бүкіл кеңістік арқылы өтетін бір ұзын орбита өте оңды (Сурет 6(b)).

• Блоктық шифрлер үшін біртипті орбиталардың (Сурет 6(с)) ансамблі дәл келуі мүмкін. Мұндай орбиталардың кеңістікте орналастырылуының кілтке тәуелділігі күрделі болуы керек; кері жағдайда, криптоанализ үрдісі кезінде ашық мәтінде іздеу кеңістігі тарыла түседі.

(а) Қысқа және болжамсыз орбиталар (криптографияға келмейді); (b) Бір ұзын орбита (лектік шифрлер үшін келеді); (с) Бірнеше біртипті орбиталар (блоктық шифрлер үшін келеді);

Сурет 5 - Хаостық және псевдохаостық жүйелердің қасиеттері

(а)	(b)	(c)

Сурет 6 - Псевдохаостық жүйелердің орбиталары