1.2.1 Криптография және хаос

1) Динамикалық жүйе. Параметрлерге тәуелді үздіксіз күйдің және үздіксіз уақыттың динамикалық жүйесі дифференциалдық теңдеумен берілуі мүмкін

мұндағы	– тегіс вектор функция,
	X – күй кеңістігі,
	К – басқарушы параметрлер кеңістігі.

Жүйе әр x₀ алғашқы шарты үшін шешімнің бар болуы және жалғыздығы шартын қанағаттандырады: , мұндағы . Бұл шешімге сәйкес келетін қисығы траектория деп аталады.

Үздіксіз күйдің (дискретті уақыттың) динамикалық жүйесі итерациялық функция арқылы [14] берілуі мүмкін

(4)

мұндағы x_i – жүйенің дискретті күйлері

φ (i, x₀) траекториясы x_ο,x_ι,x₂,... тізбегі түрінде беріледі. (4) өрнегі псевдокездейсоқ генераторларда, блоктық шифрлерде және т.б. қолданылатын криптографиялық итерацияларға ұқсас екенін көруге болады: динамикалық жүйеде де, криптографиялық жүйеде де параметрге тәуелді ақпараттың итерациялық өзгертулерімен жұмыс істейміз.

Төменде біз (X, f) жүйесін және f(x) итерациялық функциясының белгілеулерінде k параметрлерін көрсетпейтін боламыз. f(x) функциясының n-ретті қолданылуын мына түрде жазамыз

2) Хаостық жүйе. Зерттеушілер жүйеде хаостық сипаттамалар байқалатын бірнеше белгілерді атап көрсеткен [15]. Негізінен алғанда, екі классикалық қасиет қажетті шарт болып табылады, олар – топологиялық транзитивтілік және алғашқы шарттарға сезгіштік.

Анықтама (хаостық жүйе). Егер мына шарттар орындалса, динамикалық жүйе хаостық деп аталады:

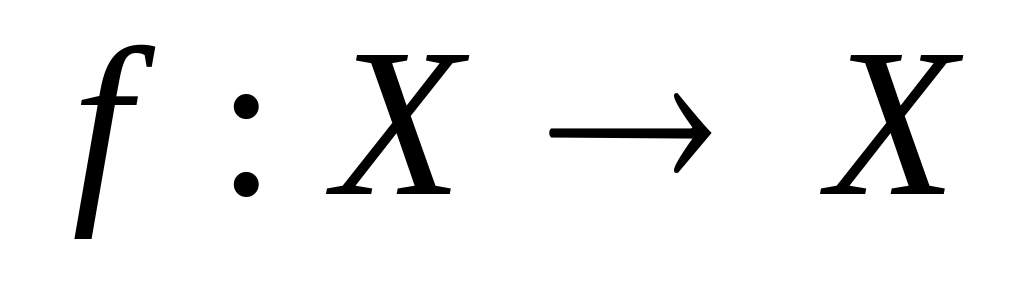1. функциясы қандайда бір метрикалық жиында топологиялық транзитивті болады, егер кез-келген ашық жиындары үшін

болатындай бар болса.

2. f функциясы алғашқы шарттарға сезгіш болады, егер кез-келген және оның H_x маңайында табылып,

теңдігі орындалатындай бар болса.

Басқаша айтсақ, егер динамикалық жүйенің траекториялары шектеулі, бірақ фазалық кеңістіктің әр нүктесінде жан-жаққа тез таралатын болса, онда бұл жүйені хаостық деп атаймыз (Сурет 2).

Жоғарыда қарастырылған криптографиялық жүйелер өздерінің талаптары жағынан хаостық жүйелерге ұқсас: топологиялық транзитивтілік, бір жағынан, криптожүйенің күйін ақпарат тасушы құралдың мүмкіндік беретін шегінде сақтау үшін, екінші жағынан, шифрленген мәтіннің бүкіл күй кеңістігін «жабу» үшін қажет. Алғашқы шарттарға сезгіштік криптожүйенің ашық мәтінге немесе псевдокездейсоқ генератордың дәнге сезгіштігімен сәйкес келеді. Сонымен, хаос теориясында да, криптографияда да біз алғашқы шарттардың сәл ғана өзгерісі бүкіл траекторияның елеулі өзгерісіне алып келетін жүйелермен жұмыс істейміз.

Сурет 2- Екі өлшемді хаостық жүйе: (а) Уақыттық кеңістік; (b) Фазалық кеңістік

3) Ляпунов экспонентасы. Хаостық жүйенің анықтамасында біз алғашқы шарттарға сезгіштік ұғымын енгіздік. Әр x₀ ∈ X нүктесі үшін анықталатын λ(x₀) Ляпунов көрсеткіші сезгіштік өлшемі болып табылады, x₀ маңайында орналасқан траекторияның экспоненциалды жан-жаққа таралу жылдамдығын көрсетеді [14]. Бір өлшемді жүйе үшін

мұндағы	ε – x0 алғашқы шарттан аз ғана ауытқу,
	n – итерациялар саны (дискретті уақыт).

Жалпы жағдайда, λ көрсеткіші x₀ алғашқы шарттарына тәуелді, сондықтанған орташаланған мәнін анықтайды. Өлшемін сақтайтын жүйелер үшін λ көрсеткіші барлық траекторияда тұрақты болып қалады. Тәжірибе тұрғысынан, Ляпунов көрсеткішін шек ретінде есептеуге болады

			(5)
			(6)

туындысы әр к аргументі x_k-ден x_k+1-ге дейін өсіп отыруына байланысты f функциясы қалай тез өзгеретінін көрсетеді. (5) және (6) шегі логарифмнің орташа мәнінің туындысына тең, және n дискретті уақыт ішіндегі траекториялардың таралу жылдамдығын көрсетеді. Көрсеткіштің оң мәні (λ>0) хаос әрекетінің индикаторы болып табылады.

d-өлшемді жүйелер үшін біз λ={λ₁, …, λ_d} жиынтығын және сапасы жағынан бір өлшемді жағдайдан еш ерекшелігі жоқ күрделірек әрекетті аламыз.

Бақылаудың рұқсат ету қабілетін (дәлдік) есепке алу үшін, бұдан артығырақ ақпаратты төменде қарастырылатын h_ks Колмогоров-Синай энтропиясы береді.

Криптография жағынан, Ляпунов көрсеткіші жүйенің криптографиялық тиімділігінің өлшемі болып табылады. λ үлкен болған сайын, ақпаратты тозаңдату (конффузия) және араластырудың (диффузия) берілген дәрежесіне жетуге қажет n итерациялар саны азая береді.

4) Бифуркация. Бифуркация (лат. bifurcus - қосарланған) деп әдетте басқарушы параметрлердің салдарынан регулярлы әрекеттен хаостыққа өтудің сапалы үрдісін айтады. Мысалға, Фейгенбаум қосарлануы бифуркацияның бір түрі болып табылады. Бифуркация нүктелерінде орнықты күйлер (периодтардың) санының қосарлануы болады. Параметр көбейген сайын қосарлану жиілей түседі, және хаостық режимге әкеледі.

Криптографияда басқарушы параметр мәнін таңдау жүйенің болжамсыздығын анынқтайды. Егер параметр кілт ретінде қолданылса, онда мүмкін болатын кілттердің кеңістігі хаостық режимге сәйкес келуі тиіс [14].