1.5.7. Статистическая обработка результатов на выдергивание шурупов из пласти образцов плиты мдф
В таблице 1.6. представлен ранжированный ряд по результатам замеров на выдергивание шурупов из пласти образцов плиты МДФ.
Таблица 1.6
Ранжированный ряд результатов замеров на выдергивание шурупов из пласти образцов плиты МДФ
Yi |
250 |
265 |
270 |
275 |
288 |
290 |
295 |
300 |
305 |
310 |
320 |
340 |
mi |
1 |
1 |
2 |
2 |
1 |
4 |
2 |
3 |
2 |
1 |
2 |
2 |
Yi |
365 |
375 |
380 |
385 |
395 |
400 |
410 |
415 |
440 |
455 |
460 |
|
mi |
3 |
2 |
3 |
4 |
1 |
5 |
3 |
2 |
2 |
1 |
1 |
|
Результат проверки грубых ошибок не выявил.
Определение среднего арифметического :
= 351,94
Определение среднего квадратического отклонения S:
= 56,13
Определение величины интервала h:
h
=
=30
В таблице 1.7. представлен интервальный вариационный ряд по результатам замеров на выдергивание шурупов из пласти образцов плиты МДФ.
Таблица 1.7
Интервальный вариационный ряд замеров на выдергивание шурупов из пласти образцов плиты МДФ
Границы интервалов |
mi |
Pi |
250-280 |
6 |
0,12 |
280-310 |
12 |
0,24 |
310-340 |
3 |
0,06 |
340-370 |
5 |
0,1 |
370-400 |
10 |
0,2 |
400-430 |
10 |
0,2 |
430-460 |
4 |
0,08 |
|
Σ=50 |
Σ=1 |
По данным интервального вариационного ряда строится гистограмма распределения величины удельного сопротивления выдергиванию шурупов, представленная на рисунке 1.8.
Рис. 1.8. Гистограмма распределения величины удельного сопротивления выдергиванию шурупов из пласти плиты МДФ
В таблице 1.8. представлены данные для построения экспериментального графика нормального распределения.
Таблица 1.8
Данные для построения экспериментального графика нормального распределения
Интервалы |
Середина интервала |
Z |
f(z) |
f(z)/S |
250-280 |
265 |
1,55 |
0,1200 |
0,0022 |
280-310 |
295 |
1,02 |
0,2371 |
0,0042 |
310-340 |
325 |
0,48 |
0,3555 |
0,0063 |
340-370 |
355 |
0,05 |
0,3984 |
0,0071 |
370-400 |
385 |
0,59 |
0,3352 |
0,006 |
400-430 |
415 |
1,12 |
0,2131 |
0,0038 |
430-460 |
445 |
1,65 |
0,1023 |
0,0018 |
Вершина кривой нормального распределения находится в точке У= ,
У=351,94, Z=0 f(z)=0,3989/56,13=0,0071
Координаты точек перегиба:
У= , У=351,94+56,13= 408,07 Z=+1 f(z)=0,2420/56,13=0,0043
У=351,94-56,13=295,81 Z=-1 f(z)=0,2420/56,13=0,0043
У= , У=351,94+56,13·2=464,2 Z=+2 f(z)=0,054/56,13=0,0009
У=351,94-56,13·2= 239,68 Z=-2 f(z)=0,054/56,13=0,0009
У= , У=351,94+56,13·3= 520,33 Z=+3 f(z)=0,0044/56,13=0,0001
У=351,94-56,13·3=183,55 Z=-3 f(z)=0,0044/56,13=0,0001
Экспериментальный и теоретический графики нормального распределения представлены на рисунке 1.9.
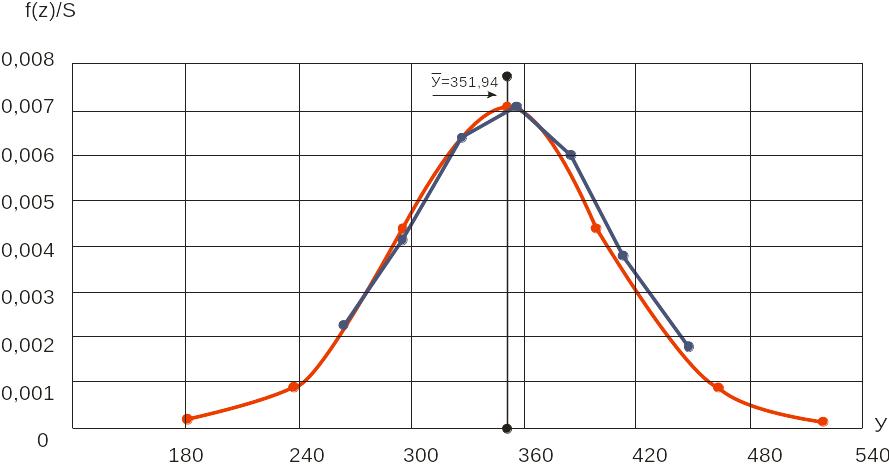
Рис.1.9. Экспериментальный и теоретический графики нормального распределения