1.5.2. Методика проведения эксперимента

В эксперименте проведены испытания следующих материалов:

• массив сосны;

• МДФ.

Данные материалы испытывались на удельное сопротивление выдергивания шурупов.

1.5.3. Испытание на удельное сопротивление выдергиванию шурупов

Для испытаний по ГОСТ 10637-78* использовались образцы плиты МДФ и массива сосны размерами 50 ×50 мм толщиной 30 мм, в количестве 150 штук.

Саморезы длиной 40 мм вворачивают в массив сосны по ГОСТ 1144-80.

Саморезы длиной 40 мм вворачивают в плиту МДФ в пласть и кромку по ГОСТ 1144-80.

Определение удельного сопротивления проводится на разрывной машине ДИ-5. Схемы определения удельного сопротивления выдергивания шурупов из пласти и кромки представлены на рисунках 1.4 и 1.5.

Рис. 1.4. Схема определения удельного сопротивления выдергивания шурупов из пласти

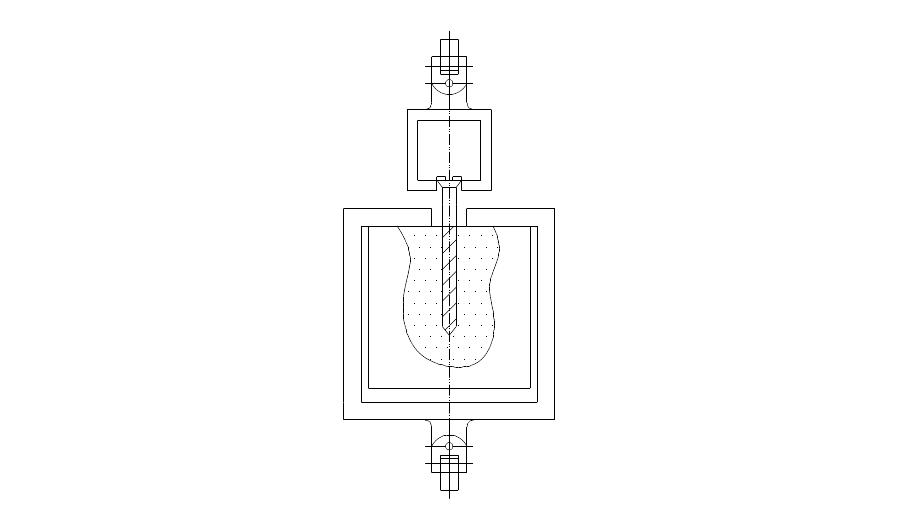
Рис. 1.5. Схема определения удельного сопротивления выдергивания шурупов из кромки

1.5.4. Метод обработки результатов эксперимента

Определение статистических показателей.

Определение среднего арифметического :

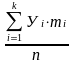, (1.1)

где k – количество членов ранжированного ряда;

n – количество замеров в выборке.

Определение среднего квадратического отклонения S:

, (1.2)

где n – 1 = f – число степеней свободы выборки.

Величина S² называется дисперсией выборки.

Проверка выборки на наличие грубых ошибок.

Абсолютно точно измерить какой-либо размер нельзя, процесс измерения всегда сопровождается ошибками. Систематические ошибки устраняются путем выверки и настройки измерительных инструментов, природа случайных ошибок неясна, а вот от грубых ошибок следует сразу же избавляться. Наиболее велика вероятность наличия грубых ошибок на границах ранжированного ряда, поэтому проверку на наличие грубых ошибок начинают с граничных, крайних элементов.

Для проверки можно воспользоваться критерием Стьюдента. В таблице распределения Стьюдента [ 3 ] по числу степеней свободы f = n – 1 и уровню значимости q (в деревообработке обычно q = 0,05) определяют табличное значение критерия Стьюдента t_табл. Для любого проверяемого элемента выборки У_i определяют расчетное значение критерия Стьюдента :

(1.3)

Если выполняется соотношение t_расч ≤ t_табл, то проверяемый результат наблюдений не является грубой ошибкой. Если t_расч >t_табл, замер является грубой ошибкой и должен быть исключен из выборки. [ 3 ]

Построение гистограммы распределения

График, построенный по данным интервального вариационного ряда, называется гистограммой. При построении гистограммы по оси абсцисс откладывают значения границ интервалов и на каждом из них, как на основании, строят прямоугольник, площадь которого равна относительной частоте Р_i соответствующей данному интервалу:

P_i= (1.4)

Так как сумма всех относительных частот равна единице, то площадь всей гистограммы так же равна единице. С увеличением числа опытов n и количества интервалов ломанная, соединяющая середины всех прямоугольников (полигон), будет все ближе к некоторой кривой, называемой кривой распределения или кривой плотности вероятности. В теории вероятностей это соотношение называется статистическим распределением. По виду гистограммы можно прогнозировать закон распределения случайной величины.

Диапазон значений выборки (ранжированный ряд) разбивается на интервалы. Величина интервала h определяется по формуле

h= (1.5)

где n – объем выборки;

У_max, У_min – максимальный и минимальный элементы выборки.

Величина интервала округляется до значений, кратных цене деления измерительного инструмента.

Начало первого интервала У₁=Уmin, конец первого интервала У₂=У₁+h. Конец первого интервала У₂ является началом второго интервала. Разбиение ранжированного ряда продолжается до тех пор, пока в последний интервал не попадет У_max . Для каждого интервала определяется частота попадания замеров в данный интервал m_i и относительная частота P_i. Результаты заносят в таблицу, на основании ее строят гистограмму.

Проверка правильности построения: Σm_i=n

Построение экспериментального графика и теоретической кривой нормального распределения

Распределение непрерывной случайной величины можно задать в виде плотности распределения вероятности. Непрерывная случайная величина У имеет нормальное распределение (распределение по нормальному закону), если плотность распределения вероятности f(у) имеет вид:

f(у)= (1.6)

где у, S- параметры нормального распределения

Если ввести обозначение, то f(у)= - плотность нормального распределения.

Нормальное распределение с дисперсией S²=1 (следовательно, и S=1) называют нормированным нормальным распределением. При увеличении среднего квадратического отклонения S, кривая нормального распределения приближается к оси У (возникает туповершинность), а при уменьшении S кривая вытягивается вдоль оси f(z) (островершинность).Максимум кривой нормального распределения находится в точке, для которой производная функции равна нулю, т.е. У=

В таблицу записывается интервальный вариационный ряд, полученный при построении гистограммы. Для каждого интервала определяется его середина:

У*= (1.7)

Затем определяется модуль Z по формуле

Z= (1.8)

_{По значениям} Z определяется плотность нормированного нормального распределения f(z), а затем вычисляется f(z)/S. По результатам расчетов строится экспериментальный график нормального распределения.Теоретическая кривая нормального распределения строится в одних координатах с экспериментальным графиком. На графике отмечается У= , максимум функции находится в точке

У= , Z=0 f(z)=0,3989/S

У= , Z=±1 f(z)=0,2420/S

У= , Z=±2 f(z)=0,054/S

У= , Z=±3 f(z)=0,0044/S

1.5.5. Результаты эксперимента на удельное сопротивление выдергиванию шурупов

Результаты эксперимента на удельное сопротивление выдергиванию шурупов для массива сосны и плиты МДФ представлены соответственно в таблицах 1.1 и 1.2.

Таблица 1.1

Результаты эксперимента на удельное сопротивление выдергиванию шурупов для массива сосны

№ образца	Р, кг.	№ образца	Р, кг.
1	140	26	170
2	250	27	210
3	265	28	235
4	138	29	140
5	170	30	265
6	230	31	158
7	195	32	195
8	120	33	184
9	235	34	138
10	150	35	250
11	210	36	190
12	267	37	210
13	140	38	135
14	265	39	144
15	184	40	230
16	275	41	198
17	280	42	198
18	190	43	162
19	205	44	190
20	267	45	270
21	144	46	250
22	190	47	135
23	235	48	184
24	198	49	205
25	158	50	235

Таблица 1.2

Результаты эксперимента на удельное сопротивление выдергиванию шурупов из пласти и кромки плиты МДФ

№ образца	Из пласти	Из кромки	№ образца	Из пласти	Из кромки
	Р, кг.	Р, кг.		Р, кг.	Р, кг.
1	290	110	16	310	145
2	385	131	27	270	150
3	250	122	28	410	120
4	320	134	29	265	130
5	365	95	30	385	95
6	400	145	31	290	140
7	270	130	32	440	134
8	410	140	33	380	110
9	300	150	34	340	122
10	275	110	35	305	131
11	380	145	36	275	150
12	385	122	37	400	98
13	288	95	38	320	158
14	295	137	39	375	134
15	340	120	40	385	120
16	380	131	41	300	144
17	400	140	42	455	98
18	290	165	43	295	122
19	300	137	44	305	144
20	440	144	45	395	119
21	365	110	46	290	137
22	400	120	47	410	150
23	415	134	48	365	165
24	375	158	49	415	140
25	460	119	50	400	120