3.3. Моделювання динаміки чисельності окремих популяцій

Експоненціальний закон

Одним із основних об'єктів вивчення у екології та біології, поведінку яких можна досліджувати за допо- могою найпростіших математичних моделей, є популя- ція — група організмів одного виду, що впродовж багатьох поколінь займає певний простір і може функ- ціонувати (розмножуватись і розвиватись) за певних умов навколишнього природного середовища. Вона є елементарною одиницею еволюційного процесу і фор- мою існування виду, множиною (групою) організмів, здатних саморозмножуватися.

Сукупність популяцій, що функціонує як цілісна одиниця у відведеному їй просторі фізичного природно- го середовища, являє собою біотичне угрупування.

Популяції мають властивості, притаманні як самій популяції (щільність, народжуваність, смертність, віко- ва структура, генетика, пристосованість), так і окремим організмам (життєвий цикл, репродукція та Ін.).

Під щільністю популяції розуміють кількість осо- бин (організмів) на одиницю площі або об'єму, напри- клад 500 дерев на 1 га, 200 кг риби на 1 га або 5 млн діа- томей на 1 м3 води. Якщо знехтувати віковими, статеви- ми і генетичними відмінностями, то щільність певного

виду досліджуваних організмів може бути повністю математично описана однією змінною величиною — кількістю особин на одиницю площі. Чисельність (щіль- ність) цих популяцій з часом зазнає змін. Навіть якщо популяцію та екосистему вважають незмінними, щіль- ність, народжуваність, рівень виживання (смертність), вікова структура, інтенсивність росту та інші характе- ристики, як правило, змінюються залежно від сезону, клімату, інших факторів навколишнього середовища.

Екологів найбільше цікавить швидкість змінювання чисельності популяції або її певної вікової групи. Серед- ню швидкість розмноження популяції визначають як відношення зміни кількості організмів (особин) ДЛ до проміжку часу Аі, протягом якого відбулася зміна (збільшення або зменшення; у разі зменшення ЛЛ'

має знак «-*). Миттєву (істинну) швидкість V =

Аі

розмноження особин, або швидкість розмноження орга- нізмів у деякий момент часу І, обчислюють як границю середньої швидкості за умови необмеженого зменшення проміжку часу Д(:

К = —=1іт-. (3.3.1)

Аі л'-о Аі 1 '

Отже, швидкість розмноження популяції є похід- ною за часом від кількості особин, що розглядається як функція часу (віку особин або віку популяції), тобто: Х~((і),У-Пі).

Крім кількісних величин при формалізації законо- мірностей розмноження популяцій розглядають т. зв. питому швидкість розмноження г, яка дорівнює зміні кількості особин за одиницю часу у розрахунку на одну особину (організм), тобто:

г = *2- . (3.3.2)

За найсприятливіших умов для розмноження попу- ляції і відсутності лімітуючих факторів швидкість зро- стання чисельності популяції може бути описана дифе- ренціальним рівнянням

^ = Ж, (3.3.3) аі

що виражає закон прямої пропорціональної залежності чи пропорціональної швидкості розмноження від кіль- кості особин (організмів) цієї популяції. Причому параметр г у рівнянні (3.3.3) називають коефіцієнтом швидкості розмноження популяції (або угруповання). Рівняння (3.3.3) вперше в 1802 р. сформулював англійський економіст і математик Томас Мальтус (1766—1834), вважаючи його універсальним законом не лише для всієї природи, а й для суспільства.

Для розв'язання (інтегрування) диференціального рівняння (3.3.3) розділимо в ньому змінні N і і, а саме:

Після інтегрування одержимо:

ІіьУ - п + Іпа, А - Іпа. З останньої рівності після потенціювання одержимо: N = ае".

Якщо відомо чисельність популяції N = N0 у почат- ковий момент часу ( = і0, то, підставивши в останню рів- ність ці значення, отримаємо:

N0 = ае"°, а - N0е'п^.

Отже, після розв'язання (інтегрування) рівняння (3.3.3) знаходимо шукану функцію:

Щі) = М0еп'-"\ (3.3.4)

де Д/0 — чисельність популяції у початковий момент часу І = і0;е = ехр — основа натуральних логарифмів, число е є неперовим числом і дорівнює е = 2,718282... ж 2,72.

Для визначення коефіцієнта г (питомої швидкості розмноження) необхідно прологарифмувати обидві частини рівності (3.3.4) і записати їх так:

ІшУ = 1п#0 + гіі- (0). (3.3.5)

За допомогою рівняння (3.3.5) можна обчислити значення г за двома відомими значеннями величин /V, і №2 у будь-які два моменти часу і0 = і, і *2(Дї2 ■ 'і ~ '2,:

г=1пДГ,-1п*, |(і_,г = Д(г- (3.з.6)

І2

Експоненціальна функція (3.3.4) добре описує роз- множення (зростання) колоній деяких бактерій до вис- наження культу рал ьного середовища (їжі). Графік цієї функції називають кривою зростання (розмноження) популяції (рис. 3.10). Кількість особин, яку визначає ця крива (3.3.4), можна також зобразити відповідно до рів- ності (3.3.5) в логарифмічному масштабі (рис. 3.11).

популяції (показникова функція) популяції (логарифмічний масштаб)

Питому швидкість розмноження — параметр г — біологічно інтерпретують як різницю між питомою швидкістю народження «Ь* (Ьігіп) і питомою швидкі- стю смертності «сі» (сіеаіп):

Показник г використовують для кількісної характе- ристики репродуктивної пристосованості організмів у генетичному розумінні І називають біотичним потен- ціалом, тобто цей показник (параметр) свідчить про вроджену властивість організмів до розмноження та виживання. У природних умовах у короткочасні періо- ди, за достатньої кількості їжі, відсутності скупченості хижаків-ворогів, часто проявляється експоненціаль- ний характер зростання чисельності популяції. Вона зростає з величезною швидкістю, хоча при цьому кожен організм розмножується з постійною швидкістю (питома швидкість розмноження є сталою г = солеї).

Багато явищ природи, наприклад «цвітіння» води у водоймищах, спалах (вибух) чисельності шкідників, розмноження бактерій та інших мікроорганізмів,

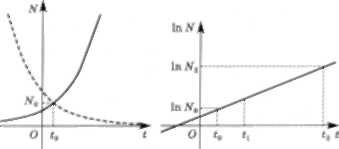
Рис. 3.10. Графік зростання

Рис. 3.11. Графік зростання

г = Ь-а\

(3.3.7)

супроводжується зростанням чисельності організмів згідно з експоненціальним законом. За неконтрольова- них сприятливих умов потомство однієї пари мух через кілька років важило б більше, ніж земна куля. Експо- ненціальний характер властивий багатьом іншим про- цесам і явищам природи, зокрема поглинанню світла, мономолекулярним хімічним реакціям, зростанню складних відсотків та ін. Проте сприятливі для розмно- ження умови не можуть довго існувати з огляду на вплив навколишнього середовища, присутність ворогів (хижаків) та інших несприятливих для життя популя- ції факторів. Взаємодія популяції з іншими та вплив зовнішнього середовища значно зменшують швидкість зростання її чисельності і змінюють закономірності роз- множення цієї популяції (угруповання). Зокрема, якщо питома швидкість смертності сі перевищує питому швидкість народження Ь, то величина г = Ь - й буде від'ємною і запис розв'язання рівняння (3.3.3) матиме такий вигляд:

N^і) = N^чі^-^, г = Ь-<і>0. (3.3.8)

Графік функції (3.3.8) являтиме собою спадну криву з асимптотою N = 0 (на рис. 3.10 — пунктирна лінія).

Логістичне рівняння

Після інтенсивного зростання чисельність популя- ції може стабілізуватися на деякому стійкому рівні, тому доцільно описувати його т. зв. логістичним рів- нянням:

^ = гЛг_Ллг*, (3.3.9) <іі К

яке часто записують так:

і^ = г„*^, ,3.3.10)

СІІ К

де г — питома швидкість розмноження; К = Л^,,, — максимально можлива чисельність популяції (угрупо- вання). На відміну від лінійного диференціального рівняння (3.3.3) рівняння (3.3.9) є нелінійним дифе-

ренціальним, а нелінійні залежності краще описують реальні об'єкти. Однак нелінійні моделі складніші, і тому їх аналіз має певні, деколи досить значні, труд- нощі.

Розділивши змінні в рівнянні (3.3.10), одержимо рівняння:

-пй, (3.3.11) яке, з огляду на співвідношення

1 1 1

ЩК - #) К(К - М) '

запишемо в такому вигляді:

(3.3.12)

( 1 * 1 |(/ЛГ га!. (3.3.13) Після інтегрування рівняння (3.3.13) отримаємо:

ІшУ - 1п(А: - И) - П + Іпа, Іпа =А, Іп-= гг + Іпа.

З останньої рівності знаходимо:

= аем. (3.3.14)

К

Якщо відомо, що при і = 0 кількість особин станови- ла N = Л/0, то за допомогою рівності (3.3.14) знайдемо параметр а:

а= ^ ■ (3.3.15) К - *0

Розв'язавши рівняння (3.3.14) відносно Л', знайдемо шукану функцію N ** ((і) у такому вигляді:

Л40 = -^^г (з.з.іб)

1 + ае

або після ділення чисельника і знаменника правої частини на є" одержимо:

а = -^— (0<а<сс). а + е К-М0 (3.3.17)

Функцію ,3.3.17) можна записати так:

*(<) = --тг-:> (3-3.18)

де стала інтегрування Ь визначається рівністю:

й = 1п- = 1п*~*° . (3.3.19) а И0

Розв'язок (3.3.18) логістичного рівняння (3.3.10)

зображується сигмоподібною логістичною кривою (рис. 3.12). Асимптотою кривої є пряма N - К.

к
1*
О		І

Рис. 3.12. Логісгична крива

Логістичне рівняння запропонував П. Ферхюльст у 1838 р. Майже через 100 років це рівняння «перефор- мулювали* Р. Перл і Л. Рід. Рівняння Ферхюльста Перла (3.3.9) враховує т. зв. ефект самоотруєння попу- ляції, або внутріпопуляційну боротьбу (конкуренцію),

яку описують членом — г--

к

Розв'язок (3.3.18)—(3.3.19) має дві важливі власти- вості:

1) при малих значеннях чисельності (або біомаси) популяції зростання відбувається за експоненціальним законом, як і у рівнянні (3.3.4);

2) з часом чисельність популяції асимптотично наближається до деякого постійного числа К (ємності середовища), перевищити яке чисельність популяції не може.

Більшість біологічних процесів за сприятливих і стабільних природних умов дуже добре описується

логістичним рівнянням, причому максимальний рівень розмноження популяції визначається ємністю середо- вища К, а швидкість розмноження (крутість сигмопо- дібної кривої і положення точки перегину М0) залежить від величини г = Ь- <і (рис. 3.12).

3.4. «Жорсткі» та «м'які» математичні моделі динаміки популяцій

Дослідження найпростіших моделей

Найпростішу математичну модель розмноження популяцій запропонував Т. Мальтус для прогнозуван- ня чисельності населення Землі:

— = гИ (г = Ь-4) (3.4.1) 41

Вона відповідає реальному процесу зростання кіль- кості особин (організмів) певної популяції тільки на початковому етапі розвитку. Значне зростання чисель- ності популяції призводить до загострення конкуренції за ресурси (їжа, простір тощо), що впливає на збільшен- ня смертності 4 і зменшення питомої швидкості розмно- ження г. Величина параметра народжуваності за- лежить від фізіологічних властивостей організмів, закладених природою.

Отже, модель Мальтуса досить «жорстка» І не може описувати зростання популяції протягом тривалого періоду. «Жорсткість» її пов'язана з параметром г, який вважають сталим. Тому «жорстку» модель Маль- туса доцільно замінити т. зв. «м'якою» моделлю

— = г(Л0ЛГ, (3-4.2) 41

де ї\Щ — змінна величина, що залежить від чисельно- сті популяції і може враховувати зворотний зв'язок:

г(Щ = Ь-аЬІ = тй-Щ-. (3.4.3)

Унаслідок цих уточнень і заміни постійного («жор- сткого») параметра г змінним («м'яким»), одержимо т. зв. логістичну модель розвитку популяції (3.3.10):

йЕ. = гітИ = (6 -аМ)М = г0 (і - !^у,К = ^лх. (3.4.4) Тут, як і в (3.4.3), для зручності покладено Ь = г0.

Побудуємо паралельно три графіки: графік залеж- ності швидкості розмноження популяції від ЇЇ чисельно- сті; фазову траєкторію; графік динаміки чисельності популяції залежно від часу (інтегральну криву) для обох моделей (рис. 3.13 і 3.14).

АУ А

ООО і а б в

Рис. 3.13. 'Жорстка" модель Мальтуса

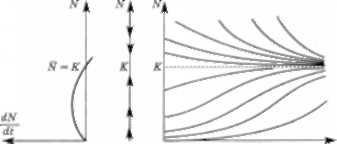
о о о

а б в

Рис. 3.14. -М'яка- логісіична модель

Для логістичної моделі в точках О і К швидкість роз- множення популяції дорівнює нулю: це стаціонарні точки. Логістична модель прогнозує, що з часом устано- влюється стійкий стаціонарний (рівноважний) режим N = К: кількість особин, що перевищує К, зменшується, а кількість особин, менша за АГ, збільшується (рис. 3.14, б). Населення Землі натепер становить приблизно б млрд осіб, стаціонарне значення, за оцінками різних учених, — 16—20 млрд осіб.

Оптимізація параметрів

для «жорстких- і «м'яких- моделей

Логістична модель значно розширює експоненціаль- ний закон. Однак вона має певні межі застосування. Нехай логістична модель (3.4.4) описує розмноження популяції риб в озері або іншій водоймі. Якщо на кіль- кість риби впливають тільки природні фактори, то за певних сприятливих природних умов її кількість можна підрахувати або спрогнозувати за допомогою моделі (3.4.4). Проте за втручання людини у розвиток риб (наприклад, якщо щорічно виловлюють г/ одиниць риби) замість моделі (3.4.4) потрібно розглянути таку модель:

^-«іЛ-ІЛ»-,. (3.4.5)

За допомогою заміни змінних

N = 1(8, г = —, я = г0КЯ (3.4.6)

рівняння (3.4.5) набуде простішого і зручнішого для досліджень вигляду:

™ = В-В'І-Я. (3.4.7) йх

Модель популяції риб (3.4.7) описує динаміку чисельності риби у нових умовах антропогенного впли- ву. Побудуємо паралельно графік зміни швидкості роз- множення, фазову пряму і графік динаміки популяції риб у нових умовах при різних значеннях інтенсивності вилову риб 0 (рис. 3.15—3.17). Прирівнявши до нуля праву частину рівності (3.4.7), знайдемо рівняння ста- ціонарного (оптимального) режиму:

о о о

Рис. 3.15. Модель при середній Інтенсивності впливу

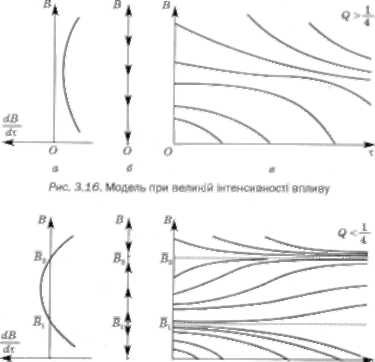
о о о

а б в

Рис. 3.17. Модель при малій інтенсивності впливу

в - в2 - ^ - о.

Корені рівняння визначають рівністю:

(3.4.8)

(3.4.9)

Різні корені рівняння (3.4.9) залежать від значень в- Так, при <3 = ~ рівняння (3.4.9) має один корінь В —

Отже, для «жорсткої» моделі (3.4.7) значення інтенсив- ності Я = — призводить до одного стаціонарного режиму: 4

початкове значення чисельності популяції В £ — з часом

2

виходить на стаціонарний режим В = ^. Однак він є

нестійким: незначне випадкове зменшення чисельності

В < — призводить до повного знищення популяції за 2

обмежений проміжок часу (рис. 3.15).

При значному вилові ф > — популяція знищується

4

за певний проміжок часу, якою б великою вона не була в початковий момент (рис. 3.16).

При малій інтенсивності вилову Я < — маємо два

стаціонарні (рівноважні) режими — В, і Вг (рис. 3.17). Стаціонарний режим при чисельності популяції В2 є стійким: чисельність популяції у цьому разі дещо менша, ніж при відсутності вилову, але вона швидко відновлюється при малих відхиленнях від рівноваги. Стаціонарний режим при чисельності популяції В, є нестійким: якщо чисельність популяції спаде, хоча б не набагато, нижче В,, то в наступний період популяція буде повністю знищена (рис. 3.17).

Оптимізація параметрів планування вилову риби призводить до цілковитого знищення жорстко регульо- ваної системи внаслідок виникнення нестійких режи- мів, боротися з якими дає змогу побудова «м'якої» моделі. Потрібно замінити «жорстке» планування вилову

■і

«м'яким», що враховує зворотний зв'язок, тобто вели- чини вилову повинна залежати від досягнутої чисельно- сті популяції. Нехай ця залежність має такий вигляд:

Я = аВ, (3.4.10)

ле параметр и (диференційована квота) підлягає вибору. У цьому разі модель (3.4.7) набуває вигляду:

«В-В-В'-оВ, ах

(3.4.11)

де о: > 0.

Стаціонарний режим В - 1 - а буде стійким при а < 1 (рис. 3.18). При стаціонарному режимі чисель- ність популяцій риб визначають за рівнянням:

тобто:

В,

в-х
1
* 1 І /	Б -1
	>-

В(1-а-В) = 0,

В0 = 1-а, 0<а<1. в і в.

В

о о

(3.4.12)

(3.4.13)

а б в

Рис. 3.18. Модель з урахуванням інтенсивності вилову

Отже, інтенсивність вилову при стаціонарному режимі:

Я = аВ0 - а(1 - а). (3.4.14,

Знайдемо значення параметра а при максимально- му вилові риби. Для цього прирівняємо до нуля похідну інтенсивності вилову (3.4.14), що розглядають як функцію параметра а:

ая

= 1 - 2а = 0 .

(3.4.15)

Звідси знаходимо:

<х = т. (3.4.16)

Отже, максимальної інтенсивності вилову фтах дося-

|, тобто Ятях=^.

Як і у разі «жорсткого* параметра ф, дослідження •м'якої» моделі, коли ■ аВ, дає той самий результат:

оптимальне значення інтенсивності Я = ~. Однак, на

4

гають при а = -, тобто ь?ша(

підміну від «жорсткого» планування вилову

(-3-

новий принцип вилову риби з інтенсивністю <3 = ссВ, що враховує зворотний зв'язок, не порушує стійкості системи (популяції), і при оптимальному зна- ченні коефіцієнта а незначні зменшення початкової чисельності риби щодо стаціонарного режиму В - В0 = — 1 - а зумовлюють автоматичне відновлення стаціо- нарного режиму природою самої системи (рис. 3.18, в). Незначне відхилення коефіцієнта а від оптимального

а = — не призводить до самознищення популяції, а 2

лише зменшує величину прибутку (інтенсивність вило- ву (?). Результати таких досліджень «м'якої» (гнучкої) моделі справедливі і для складніших «м'яких» моде- лей. Тому прості «м'які» моделі корисні для моделю- вання багатьох складних процесів і управління (регу- лювання) ними.