
- •Тема 8. Математичне моделювання і прогнозування..
- •6.1. Моделювання основних процесів життєдіяльності рослин
- •6.3. Математичне моделювання процесу поглинання важких металів ґрунтом і рослинами
- •6.4. Математичне моделювання впливу осолонцювання та засолення грунту на розвиток рослин
- •6.5. Визначення виносу
- •7.1. Загальний вигляд математичної моделі динамічної системи з розподіленими характеристиками
- •7.2. Побудова моделей масопереносу в нерухомому та рухомому середовищах
- •7.3. Одновимірні моделі розповсюдження речовини в нерухомому середовищі
- •1. Відомі значення концентрацій забруднення на ме- жах ділянки (озера), де воно розповсюджується:
- •Тема 10
- •3.1. Похідна, її застосування при вивченні законів природи. Операції диференціювання та інтегрування
- •3.3. Моделювання динаміки чисельності окремих популяцій
- •3.5. Динаміка біоценозів
- •3.6. Моделювання трофічного ланцюга
- •3.7. Моделювання динаміки риб і їх паразитів в умовах токсичного забруднення водного середовища
Тема 10
Застосування диференціальних рівнянь при моделюванні екологічних процесів
Метод теорії диференціальних рівнянь с найефек- тивнішим методом побудови математичних моделей, що описують динаміку екосистем, враховуючи взаємодію як між окремими елементами екосистеми, так і між еле- ментами екосистеми І зовнішніми факторами середови- ща, в якому функціонує кожен елемент екосистеми. Ці рівняння можуть описати різні види динаміки біологіч- них і екологічних процесів, побудувати математичні моделі розвитку окремих популяцій і біоценозів.
3.1. Похідна, її застосування при вивченні законів природи. Операції диференціювання та інтегрування
Задачі, що допомагають усвідомити роль похідної
Розумінню суті поняття «похідна» сприятиме розв'я- зування певних задач.
Задача про дотичну до кривої. В елементарній мате- матиці розглядають дотичну до кола як пряму, що має з
колом одну спільну точку. Якщо розглядати будь-яку криву, яка є графіком деякої заданої на відрізку [а. Ь] функції (рис. 3.1)
У-Г(х), (3.1.1)
то таке визначення дотичної не підходить. Справді, для параболи можна провести безліч прямих, що мають одну спільну точку з крипою (параболою), але вони не будуть дотичними. Отже, узагальнене визначення дотичної до кривої в даній точці має бути таким: дотич- ною до кривої в даній точці М0(х0, у0) називають гранич- не положення січної МдМ, коли точка М наближається до точки М0.
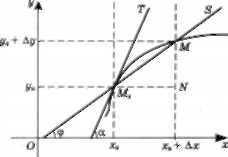
Рис, 3.1. Графік до визначення похідної через дотичну
Проведемо через точку М0(х0, у0) дотичну М0Т до перетину з віссю Ох. Позначимо кут нахилу до осі абс- цис через а, а кут нахилу січної М0М до осі абсцис — через <р (рис. 3.1). Використавши рисунок, визначимо кут ф, або ДОр:
Ау _ /(£±Д£Ь^£)_ (312)
Ах Ах
Якщо точка М, рухаючись по кривій, наближати- меться до точки Мй (Ах —> 0), то величина кута ф буде прямувати до кута а, а І£ф —* 1&а. Звідси випливає, що тангенс кута нахилу дотичної до осі Ох у точці М0(дг0, у0) визначають за такою рівністю:
і%а = Ііт ^ , (3.1.3)
ЛІ-.0 Ах
або
Іца = Ііт
Ді-*0
Г(х + Ах)-Пх) Ах
(3.1.4)
Як відомо, тангенс кута нахилу прямої до осі абсцис називають кутовим коефіцієнтом к (див. розділ 2.2).
Отже, щоб записати рівняння дотичної до кривої у = Цх)у точці М0(х0, у0), потрібно скористатися рівнян- ням прямої, що проходить через дану точку:
(3.1.5)
де кутовий коефіцієнт к = ї%<х визначають за рівністю (3.1.4).
Задача на визначення швидкості тіла, що рухається нерівномірно. Розглянемо спочатку тіло, що рухається рівномірно по прямій ОЗ (рис. 3.2). Швидкість руху тіла V у цьому разі дорівнює шляху 5, пройденому тілом за одиницю часу:
V =
8і 30 3 30
'і- 'о
= — = сопзЬ. (3.1.6) Аі
5. - 5(М
5 " $(')
5,-5(ї,)-5((+Д0
Рис. 3.2. До визначення поняття -похідна- {фізичний зміст)
Якщо тіло рухається нерівномірно, тобто за рівні проміжки часу проходить різні відстані, то відношення (3.1.6) характеризує середню швидкість руху тіла. Оче- видно, чим менший проміжок часу Аі ■ і ~ (0, а отже, і проміжок шляху Д5 = 5 - 50, тим більше середня швид- кість У^р наближатиметься до справжньої (реальної) швидкості, яку також називають миттєвою швидкістю у даний момент часу. Отже, якщо пройдений тілом шлях 5 задано як функцію від часу і, то середню швид- кість руху Ксер на проміжку часу від І до ( + Д( визнача- ють за відношенням (рис. 3.2)
у Д5 5,-5^ З(і + Аі)~8(і)
елр~ Аі' Аі Аі
а миттєву швидкість (швидкість) руху тіла в момент і встановлюють унаслідок граничного переходу:
хг Д§ ,. 5(г + Дї)-5(г)
V = Ііт — = Ііт —---—. (3.1.8)
&х->0 Д( лл-»0 Д/ '
Задача хімічної кінетики. Швидкість хімічних реакцій і проміжні та кінцеві продукти (речовини), утворені під час протікання цих реакцій, вивчає розділ фізичної хімії хімічна кінетика. Нехай у момент 10 про- тікання реакції перетворення речовини А на речовину В маса речовини, що прореагувала, становила т0, а через деякий час АІ маса речовини А стала дорівнювати т1. Отже, за час від і0 до („ + АІ прореагувала маса речови- ни, що дорівнює Ат = лі| — т0. Швидкістю хімічної реакції називають кількість (масу) речовини Ат, що вступила в реакцію або утворилась внаслідок реакції за одиницю часу в одиниці об'єму. Оскільки реакція відбу- вається нерівномірно, то справжню (дійсну) швидкість УА можна визначити тільки за допомогою вже відомої рівності
Ата ,. Де.
А
V = пт ^ІІІА. = ат І^А . (3.1.9)
Дї»0'И7дД/ &х-'0 АІ
Під концентрацією с речовини розуміють кількість (масу) речовини в одиниці об'єму, тобто:
с. = , св , (3.1.10)
де УГА — об'єм речовини А, що прореагувала; \¥в — об'єм речовини В, що утворилась.
Означення похідної та невизначеного інтеграла
Якщо на проміжку (а, Ь) задано функцію у = і(х), то границя відношення приросту функції Ау до приросту аргументу Ах, за умови, що приріст аргументу прямує до нуля, є похідною функції ((х) по аргументу дг.
Для похідної застосовують такі символічні позна- чення:
у- = №) - ІШ *± - Ііт А** (3.1.11)
&х-*0 Ду Дг-'О Ду
або
&-1ІЛ. І****-™. ,3.1.12)
(ІХ Лх-'О Ах
Позначення у' = і"(х) запровадив французький мате- матик Жозеф-Луї Лагранж (1736—1813), а позначення
— — німецький математик Готфрід-Вільгельм Лейбніц сіх
(1646—1716). Англійський математик і механік Ісаак Ньютон (1643—1727) позначив похідну, як у = і{х). Вживаються також позначки: у'„ (/,'тощо. Операцію зна- ходження похідної даної функції називають диференці- юванням.
Якщо дана функція г залежить від аргументів дг і у, то запроваджують поняття «частинний приріст функції».:
Ахг = /{х + Дх, у) - /(х, у); (3.1.13)
V " Л*. У + Пх, у), (3.1.14)
а також «частинні похідні»:
4 ■ І», и, + (3.1Л5) г. *1=1ітГ(х,У + &У)-Нх.у) (3116)
сіу Лу-»0 Ау
За допомогою формул (3.1.11)—(3.1.16) можна знай- ти похідну від будь-якої елементарної функції однієї змінної або частинну похідну функції двох незалежних змінних.
Якщо задано похідну:
Пх) = Г(х), (3.1.17)
а потрібно знайти функцію Р(х), то таку обернену до диференціювання операцію знаходження функції за її похідною називають інтегруванням. Функція Р(х) називається первісною, а сукупність Г(х) + С усіх первіс- них — невизначеним інтегралом від функції /(х);
Щх)сіх = Р(х) + С, (3.1.18)
де знак 1, який ввів Лейбніц, називається інтегралом, {(х) — підінтегральною функцією, /(х)<2х — підінте- гральними виразом, х — змінною інтегрування, С — сталою (С ■ сопзі). У табл. 3.1 приведені похідні Й інте- грали основних елементарних функцій.
Таблиця 3.1
Похідні та Інтеграли основних елементарних функцій
Функція |
Похідна |
Інтеграл |
у — а - С0П8І |
у' = 0 |
|оі(х = ах +С |
|
у' = лх" 1 |
(1.1 л -1-і |
|
і/" |
|е"<*х = е" +С |
у-а" |
у' - а'іпа |
-1 Іпа |
у ~ Іоках |
X |
|іпхо*х = ХІПХ-Х + С |
У " Іпх |
х |
Іт— |
у - зіпх |
І/' - соз* |
|8Іп.<Л: = -008л+С |
у - СОЗІ |
у' - -віпх |
|созхо*х = зіпх + С |
У = чг* |
*—*г- СОЗ X |
^ соз х |
у - сіеж |
31ІЇ*Х |
л зіігх |
У - «V |
о*' = и'и + ии' |
^иа~и = ио - ^йи |
N |
, и'о - ои' |
|хсова'х = хвіїїх »созх + С |
•/ - Я"(*)ї |
у' = Г(и)*іНх) |
{хе'гіх = хе" -е' *С |
Рівняння (3.1.17) з похідною невідомої функції у = /(аг) називають диференціальним рівнянням. Розв'я- зати диференціальне рівняння означає знайти невідому функцію у = /(дг) або сімейство функцій /(дг) + С, які задовольняють дане диференціальне рівняння, напри- клад рівняння (3.1.17).
Приклади застосування похідної при моделюванні біологічних, хімічних і фізичних процесів
Розглянемо кілька прикладів побудови простих математичних моделей за допомогою похідної і дифе- ренціального рівняння.
Приклад 1.
Деяка кількість бактерій АГ© перебуває у сприятли- вих умовах. Шляхом експериментальних досліджень установлено, що швидкість розмноження таких бакте- рій пропорціональна їх кількості. Знайдемо залежність кількості бактерій від часу, за умови, що швидкість
(Ш
розмноження визначається як похідна
Отже, можна записати рівняння:
Ц- = Ж, (3.1.19) аі
де коефіцієнт пропорціональності г залежить від виду бактерій і називається коефіцієнтом, або константою, швидкості розмноження бактерій.
Розділяючи змінні в (3.1.19) та інтегруючи, одержимо
N
(3.1.20)
або
Звідси
ІпА/ = п + 1па, А = \па. (3.1.21)
N(1) = ае", а = СОП8І. (3.1.22)
Скориставшись додатковою інформацією
*(0) = ^0, (3.1.23)
рівність (3.1.22) запишемо в такому вигляді:
Щі) = И0е". (3.1.24)
Щоб визначити сталу г, потрібно знати кількість бактерій у будь-який момент часу г — ї,. Нехай відомо
Щі\)~Ях. (3.1.25)
Підставивши (3.1.25) в (3.1.24), одержимо:
Л^А^е"' (3.1.26)
Прологарифмуємо ліву і праву частини рівності (3.1.26):
1піУ,-1п#0+г*,. (3.1.27) Звідси знаходимо шукане значення константи г:
, = (3.1.28, 'і
Отже, формулу (3.1.24) можна записати так:
У<гі = ЛГ0 ехр'"*■-"'*'> і, (3.1.29)
де символом ехр позначено експоненціальну залеж- ність — ехр = е = 2,72.
Приклад 2.
Згідно Із законом хімічної кінетики (законом дію- чих мас), швидкість протікання реакції пропорціональ- на масі або концентрації речовини, що вступає в реак- цію, тобто:
иА--ксА (3.1.30)
або
ов = ксА> (3.1.31)
де сА — концентрація речовини А, причому речовина А перетворюється на речовину В. Знак мінус у правій частині рівняння (3.1.30) означає, що кількість речови- ни А зменшується. Якщо використати поняття похід- ної, то швидкість протікання хімічної реакції є похід- ною від маси або концентрації за часом. Тому рівняння (3.1.30) і (3.1.31) можна записати у вигляді диферен- ціальних рівнянь:
^- = -ксА, (3.1.32) аі
^- = ксА, (3.1.33)
де А — коефіцієнт пропорціональності, який встановлю- ють для кожної речовини, що вступає в реакцію, на основі експериментальних даних; с„ — концентрація речовини В.
Розв'язуючи (інтегруючи) диференціальне рівняння (3.1.32), одержимо:
•-л
Щоб визначити постійні а і к, що входять до правої частини рівності (3.1.34), потрібно знати концентрацію речовин А і В до початку реакції. Нехай відомо
сА(0) = с(0) = сО. (3.1.35)
Враховуючи (3.1.35) і (3.1.34), маємо:
а = с0. (3.1.36)
Отже, ця реакція відбувається за таким законом:
сд(г) = с0е". (3.1.37)
Щоб знайти концентрацію речовини В, потрібно переписати рівняння (3.1.33) з урахуванням співвідно- шень (3.1.34) і (3.1.36):
^ = кс0еГ*. (3.1.38)
Після інтегрування (3.1.37) одержимо:
св(і) - с0е-*' + о. (3.1.39)
Враховуючи, що св(0) = 0, знайдемо:
св(0) = -с0 +■ Ь - 0; Ь - с0. (3.1.40)
Отже, формула (3.1.39) матиме такий вигляд:
св(і) = -с0(1-е"), (3.1.41)
де к — стала швидкості протікання реакції для даної речовини.
Приклад 3.
Похідну від похідної називають другою похідною, або похідною другого порядку, і позначають так:
у', Г(х), х(і), ухж; У&. (3.1.42)
Отже, друга похідна показує швидкість змінювання першої похідної. Зокрема, якщо розглядати рух тіла при вільному падінні, то другу похідну визначають як похідну від швидкості руху тіла, тобто друга похідна від шляху, пройденого тілом, по часу є прискоренням рухо- мого тіла. Оскільки експериментально встановлено, що прискорення тіл при вільному падінні є величиною ста-
лою і дорівнює £ = 982 см/сек2, то можна скласти рів- няння:
або
= 8- (3-1-44)
Інтегрування рівняння (3.1.44) один раз дає:
— = 8* + С., С.=соп5І. (3.1.45) йі
Після інтегрування рівняння (3.1.45) одержимо:
8(1) = ^- + С,* + С2. (3.1.46)
Щоб рівняння (3.1.46) описувало рух конкретного тіла, потрібно знати його початкове положення і почат- кову швидкість. Нехай відомо:
5(0) - 50, о(0) = о0. (3.1.47)
Враховуючи додаткові дані (3.1.47) та рівняння (3.1.32) і (3.1.33), знайдемо:
и(0) = С, = у0, 5(0) = Сг = 50. (3.1.48)
Отже, формула (3.1.46), за якою визначають поло- ження тіла при вільному падінні, матиме вигляд:
5(г) = ^- + [;пГ + 5п • (3.1.49)
Знаходження невідомих параметрів
під час верифікації математичних моделей
У процесі побудови математичних моделей виникає необхідність знаходження (визначення) невідомих параметрів (сталих) у складі цих математичних моде- лей. Причому ці параметри у фізичних моделях мають певний фізичний (екологічний) зміст, аут. зв. стати- стичних моделях не мають його. Процес встановлення числових значень параметрів математичної або імітацій- ної моделей називають верифікацією, або калібровкою
моделі. Завдання полягає в тому, щоб знайти числові значення параметрів моделі на основі даних натурних спостережень або лабораторних експериментів. Модель вважають верифікованою, якщо результати двох послі- довних розрахунків збігаються з необхідною для прак- тики точністю. Числові значення параметрів визнача- ють у такий спосіб, щоб різниця між даними натурних чи лабораторних експериментів і розрахунковими зна- ченнями змінних величин була мінімальною, тобто в більшості випадків для знаходження невідомих параме- трів моделі застосовують метод найменших квадратів або метод середніх.
Розглянемо деякі найпростіші способи визначення невідомих параметрів математичної моделі, записаної у вигляді функціональної залежності:
с(г) = /(а, р,у, (), (3.1.50)
де с — концентрація, чисельність або біомаса; і — час; а, (і, у — невідомі параметри з певним фізичним (еколо- гічним) змістом або без нього у статистичних моделях.
Математична модель може бути побудована у вигля- ді одної функціональної залежності типу (3.1.50) або у вигляді кількох функціональних залежностей типу (1.4.11), де о,, і>2, і>т — невідомі параметри, які пот- рібно визначити на основі даних натурного або лабора- торного експерименту.
Припустимо, що числові значення параметрів моде- лі відомі. Тоді за допомогою даної математичної моделі для будь-якого моменту часу і для кожної точки просто- ру (у випадку просторової математичної моделі) можна встановити значення невідомих функцій — компонен- тів певної екологічної системи або характеристик дослі- джуваного екологічного процесу. При невідомих число- вих параметрах необхідно знати значення функцій для певних значень часу І для координат точок у просторі. Ці значення можна отримати лише на основі експери- ментальних даних. Отже, у цьому разі слід розв'язати т. зв. обернену задачу: за даними значеннями аргумен- тів і функцій, що визначаються певним рівнянням або системою рівнянь, знайти невідомі параметри (констан- ти) у складі даного рівняння або системи рівнянь.
Пояснимо процедуру встановлення невідомих пара- метрів у разі, коли математичну модель представлено у
вигляді одного функціонального рівняння з трьома невідомими параметрами типу (3.1.50). Щоб визначити параметри а, р і у, необхідно мати три рівняння, які одержують, якщо для трьох будь-яких значень аргу- менту ї,, і2 і і3 на основі експерименту встановлено три значення функції С,, С2 і С3.
Підставивши ці значення аргументу і функції в рів- няння (3.1.50), отримаємо систему рівнянь:
С, «/(а, р, у,*,),
С2 = Г(а, Р,у, і2), (3.1.51) С3 - /(а, р, у, ї3),
де а, р і у є невідомими. Якщо система рівнянь має розв'язок, то, розв'язавши її, знайдемо невідомі пара- метри а, Р і у.
Експериментальні дані не можуть бути точними. їх похибка є різною для різних значень параметрів, причо- му заздалегідь ніколи не відомо, які з експерименталь- них даних визначені з більшою, а які з меншою точні- стю. Тому, якщо даних експерименту більше, ніж пара- метрів, то з них можна обрати будь-які три, щоб скласти три рівняння типу (3.1.51). Очевидно, якщо є п даних, а визначити потрібно т параметрів (т < п), то макси- мальна кількість різних систем 5т з т рівнянь дорівнює кількості комбінацій з п ПО ЛІ елементів:
5т = С = ^ = вї . (3.1.52)
Отже, розв'язавши 5т рівнянь для кожного з т параметрів, матимемо 5Ш значень. Зокрема, у разі трьох параметрів а, Р і у, якщо на основі експериментальних спостережень маємо чотири значення аргументу і чоти- ри значення функції, пов'язані рівнянням (2.8.46), то, згідно з формулою (3,1.52), кількість систем для визна- чення шуканих трьох параметрів становить:
Розв'язавши чотири системи рівнянь, знайдемо чотири значення кожного з параметрів
а„ а2, а3, а„ р„ р2, р3, р„ і у„ у2, у3, у«, (3.1.54)
причому невідомо, яке із значень знайдених параметрів є найточнішим. Тому доцільно шукані значення пара- метрів визначити як середні арифметичні значення одержаних чотирьох значень (3.1.54):
а, |
+ а: |
|
+ а4 |
|
|
4 |
|
Р,- |
►Р> |
+ РЯ- |
|
|
|
4 |
» |
Уі - |
|
+ ЇЯ-» |
"Ті |
(3.1.55)
4
Якщо кількість даних експерименту перевищує кількість параметрів, можна визначити невідомі пара- метри методом найменших квадратів або методом серед- ніх (пункт 2.8). У цьому разі бажано, щоб невідомі пара- метри входили до рівнянь (3.1.51) лінійно або рівняння можна було б звести до лінійного.
У разі, якщо математична модель побудована у вигляді диференціального рівняння або системи дифе- ренціальних рівнянь, перед визначенням невідомих параметрів слід розв'язати диференціальні рівняння, тобто представити математичну модель у вигляді функ- ціональної залежності між невідомими змінними вели- чинами — компонентами вектора стану досліджуваної системи або процесу.
Часто диференціальне рівняння або система дифе- ренціальних рівнянь не можуть бути розв'язані аналі- тичними методами, тобто їх розв'язок не виражається елементарними функціями. У цьому разі невідомі пара- метри у складі диференціальних рівнянь визначають за чисельними методами розв'язування диференціальних рівнянь, які дають змогу отримати розв'язок диферен- ціальних рівнянь у вигляді таблиці чисел, за яким можна визначити невідомі параметри (обернена задача).
Застосуємо для визначення параметрів найпрості- ший чисельний т. зв. різницевий метод.
Нехай математична модель представлена у вигляді одного диференціального рівняння з двома параметрами:
с/г
— = /(а,р,0- (3.1.56)
Щоб скористатися даними натурних або лаборатор- них експериментів, потрібно похідну в рівнянні (3.1.56) замінити різницевим відношенням
£«^.5*1^-0.2.8.....п. (8.1.67)
Отже, рівняння (3.1.56) перепишемо у такому вигляді:
^ = /(а,іи), (3.1.58)
або
Де, - і(а, Ь, г,)Дг(, і - 0, 2, 3.....п, (3.1.59)
де п — кількість експериментальних даних. Для визна- чення параметрів а і Р з рівняння (3.1.59) потрібно не менше трьох експериментальних даних /„, с0, і,, с}, 12, с2, які підставляють в рівняння (3.1.59) для одержання системи двох рівнянь з двома невідомими а і р. Якщо даних більше, ніж три, то для визначення параметрів а і р отримаємо більше трьох рівнянь.
Після визначення невідомих параметрів, наприклад параметрів а, Р і у математичної моделі (3.1.51), модель вважають верифікованою. При цьому слід зважати на те, що параметри визначені з певною похибкою, а тому за допомогою математичної моделі значення шуканої змінної величини обчислюється теж з певною похибкою щодо експериментальних даних.
Позначимо експериментальні дані через с,, с2, с~3, ...,с„. Тоді абсолютну середню похибку обчислюють за допо- могою рівності:
ДСд>г.І+КІ+КІ+---+КІі (ЗЛ.60)
п
а абсолютну середню квадратичну похибку — із засто- суванням рівності:
^=<^^Б^ІШ., (3.1.61)
де:
Де, =с, -с„ Дс2 - с2-с2.....Дс„ - с„ -с„. (3.1.62)
Середню арифметичну відносну похибку визнача- ють рівністю:
дос
середнє арифметичне експериментальних даних:
(3.1.64,
Середню квадратичну відносну похибку встановлю- ють за допомогою рівності:
8~ = ,7І^
і 1
Де,
або у відсотках
6. = юо% 1-Х
Де,
(3.1.65,
(3.1.66)
Найчастіше для визначення абсолютної і відносної похибок використовують відповідно формули (3.1.61) і (3.1.66).
Можна обчислювати абсолютну і відносну похибки не тільки як середні, а й у окремих точках, які при дос- лідженні представляють особливий інтерес, а також знаходити найбільші і найменші абсолютну і відносну похибки. Метод підбору дає змогу уточнювати значення невідомих параметрів.
3.2. Загальні принципи моделювання екологічних систем за допомогою диференціальних рівнянь, стаціонарні розв'язки та їх стійкість
Загальний вигляд математичної моделі
При побудові математичної моделі реальної еколо- гічної системи застосовують певні математичні символи для позначення змінних і постійних величин, що харак- геризують кількісні властивості цієї системи. Як прави-
ло, змінними величинами є скалярні функції часу, які описують чисельність, біомасу або густоту досліджува- ної популяції, біоценозу тощо. Математичну модель вважають побудованою, якщо знайдено функції Р — {^\, Р2, .... Рр), що визначають характер зміни в часі (дина- міку) основних компонентів екосистеми, числові харак- теристики яких позначимо через с,(і), ег{і), с3(1), ...£„(()• Вектор с(г) = (С|, с2, .... с„) називається вектором стану екосистеми. Невідомі функції С] ~ Рі(і), са ■ Ргі*)* с9 = Р&(1), ...» ся = Р„(і), знаходять з деякого співвідно- шення виду (1.4.10). Однак найчастіше таким співвід- ношенням є одне або кілька (система) диференціальних рівнянь, де невідома функція входить під знак похідної.
У загальному випадку математична модель, побудо- вана за допомогою звичайних диференціальних рів- нянь, має такий вигляд:
де с,(0> с2(і), Сь(1), ...с„(і) — невідомі функції часу, що описують показники (характеристики) компонентів
. .. 4с, . .
екологічної системи; —'- — швидкості зміни показників
41
екосистеми (концентрації речовини, чисельності або біо- маси організмів); [{ — функції, які залежать від зовніш- ніх і внутрішніх параметрів екосистеми (]= 1, 2, 3,п).
Функції /, можуть бути лінійними і нелінійними. Якщо функції Д не залежать явно від часу г, то систему рівнянь (модель) називають автономною (динамічною або консервативною) і записують так: 4с, , .
-^ = /І(с„с2,...,сі,)ї 4с2
Аі ~'Лсі'сг>(3.2.2)
ас
7 = ЇЛСі^2.....О-
Якщо правою частиною системи (3.2.1, є лінійні функції, то відповідну систему рівнянь називають лінійною і записують у такому вигляді:
^ = +аіг^2 +.» +
<^Є? , І.\
^ = ял|с,+ая2с2+...+аплсл + /я(г). аі
Лінійні диференціальні рівняння не завжди можуть детально описати складні екологічні процеси, що потре- бують глибокого дослідження та аналізу. Однак у багатьох випадках доцільність їх використання для вивчення екологічних систем і процесів не викликає жодних сумнівів. До того ж методи розв'язування лі- нійних диференціальних рівнянь розвинуті значно краще, ніж нелінійних.
За необхідності моделювання поведінки (стану, еко- системи або її окремих компонентів при змінних у часі зовнішніх умовах (наприклад, таких, що змінюються періодично або випадково, завдання полягає у вивченні неавтономних систем (3.2.1, або (3.2.3,. При цьому спо- чатку будують і досліджують автономну систему (мо- дель). Потім, з огляду на характер змінних зовнішніх умов, або додають до правої частини рівнянь (3.2.2) нові члени, залежні явно від часу, або постійні коефіцієнти замінюють змінними, залежними від часу.
Завдання моделювання полягає в тому, щоб розв'я- зати систему диференціальних рівнянь (3.2.1), (3.2.2) або (3.2.3), тобто знайти невідомі функції:
с, = Л(0. с2 = Р2(і),.... сп = Рп(1), (3.2.4)
які б задовольняли відповідні диференціальні рівняння і додаткові (початкові) умови:
*і(*о) = сю> с2(і0) = с20,сп(10) = сп0. (3.2.5)
Функції (3.2.4) називають розв'язками, або інте- гралами, диференціальних рівнянь, а їх графіки, побу- довані в (л + 1) просторі, називають інтегральними кривими.
У загальному випадку знайти аналітичні розв'язки нелінійних систем (3.2.1) або (3.2.2) не завжди можли- во. Однак наближені (чисельні) розв'язки можна зна- йти майже завжди за допомогою сучасних чисельних методів і ЕОМ. Водночас іноді доцільно не знаходити точний або наближений розв'язок, а обмежитись якіс- ним аналізом шуканих розв'язків і з'ясувати найцікаві- ші властивості динаміки системи, зокрема умови її рів- новаги і стійкості. Для цього застосовують спеціальну якісну теорію диференціальних рівнянь, на окремих положеннях якої слід зупинитися.
Основний підхід у якісній теорії диференціальних рівнянь полягає в тому, що стан динамічної системи (екосистеми) характеризується змінними сх, е2, с3,.... сЯУ які в кожний момент часу набувають певних значень відповідно до системи (3.2.2). Якщо в л-мірному просто- рі відкласти на осях координат значення змінних сх, сг, с3, .... с„, то стан системи характеризуватиме точка М(сх, с2, с3,.... с„), яка в просторі буде описувати деяку криву. Цю криву називають фазовою траєкторією системи (3.2.2), а простір, в якому вона проходить, — фазовим простором автономної системи (3.2.2).
Будь-яка фазова траєкторія належить до певного типу:
1) гладка крива без точок самоперетину;
2) замкнута крива (цикл), що описує періодичний процес;
3) точка, що відповідає положенню рівноваги системи. Якісна теорія диференціальних рівнянь дає змогу
описувати поведінку фазових траєкторій і досліджува- ти реальні системи (екосистеми). Сукупність фазових траєкторій, що вІдповідаюіь різним початковим умо- вам, називають фазовим портретом системи (3.2.2).
Фазові траєкторії, на відміну від інтегральних кри- вих, несуть неповну інформацію про досліджувану систему. Проте в багатьох випадках достатньо знати поведінку (структуру) фазових траєкторій. Фазова траєкторія для одного диференціального рівняння являє собою пряму, яка називається фазовою прямою.
Важлива властивість автономної системи (3.2.2) полягає в тому, що вона може мати стаціонарні розв'яз- ки, які визначають стан рівноваги реальної системи або процесу. У стані рівноваги псі показники екосистеми
С[, с'2, С3, с* не змінюються в часі, тобто не залежать від нього. Тому в стаціонарному стані всі похідні за часом у системі (3.2.2) дорівнюють нулю. Отже, прирів- нявши до нуля праві частини рівнянь (3.2.2), одержимо систему алгебраїчних рівнянь для визначення стаціо- нарних значень є], с'2, с'3,.... с*:
№*.<.<£.....<)-0:
Точку фазового простору М(с,\ ...» О називають стаціонарною (особливою) точкою, або точкою рівно- ваги системи.
Стійкість стаціонарних розв'язків
Після знаходження стаціонарних розв'язків авто- номної системи (3.2.2) постає питання про їх стійкість, а отже, про стійкість рівноважної реальної системи. Якщо при незначному початковому відхиленні від стану рівноваги система (розв'язок) ніколи не відхи- ляється далеко від цього положення, то стан рівноваги є стійким і відповідає стійкому стаціонарному режиму функціонування реальної системи. Виведення системи зі стану рівноваги з подальшим відхиленням від цього стану відповідно до рівняння (3.2.2) свідчить про нестійкий стан рівноваги.
Поняття стійкості легко пояснити на прикладі меха- нічної стійкості. Розглянемо металеву кульку, що котиться по хвилястій поверхні (рис. 3.5). Для кульки є два положення рівноваги: коли вона перебуває в най- нижчій точці поверхні (на дні впадини х = хх) і коли роз- міщується в найвищій точці поверхні (наприклад, на вершині гірки х = х2). Положення рівноваги кульки у найнижчій точці є стійким (невеликі відхилення куль- ки спричинять затухаючі коливання навколо положен- ня рівноваги), а в найвищій — нестійким (незначні від- хилення кульки призведуть до її великого зміщення, і вона або переміститься у найнижчу точку, перше поло- ження, або віддалятиметься на нескінченність).

о
і - х
X- X,
X
РИС. 3.5. МеханІЧНИЙ ЗМІСТ ПОНЯТТЯ -СТІЙКІСТЬ'
Значний інтерес представляють дослідження стійко- сті екологічних систем, які теж можуть мати стійкі і нестійкі положення рівноваги. Нестійкі положення рів- новаги з часом можуть переходити у стійкі або система може набути нереальних (критичних, форм або, нареш- ті, може загинути. Всі ці випадки описують точковими математичними моделями, побудованими за допомогою звичайних диференціальних рівнянь та їх систем. У разі, коли моделююча система описується одним дифе- ренціальним рівнянням виду:
питання про стійкість положення рівноваги системи можна розв'язати, досліджуючи поведінку функції {(с),
.. йс _
тобто характер зміни похідної —. За означенням, у
Аі
стаціонарній точці с = с похідна дорівнює нулю:
Дослідимо як змінюються розв'язки (інтегральні криві, с„ - Ф„(0 в околі точки с — с залежно від значень похідної /(с„) при с„ < с і с„ > с', і побудуємо фазові прямі. Для цього розглянемо три випадки.
1. Нехай відомо, що в околі положення рівноваги с похідна /(с) змінює знак з « + » на «-» при зростанні с.
![]()
(3.2.7)
Г(с') = 0.
(3.2.8)
Тоді при сп < с' маємо
> 0, а це означає, що всі значен-
ня с„, розміщені нижче від прямої с - с, збільшуються,
тобто прямують до с*. Якщо с„ > с, то —— < 0 , а цс озна-
аі
чає, що всі значення с„, розміщені вище від прямої с — с , зменшуються, тобто теж прямують до с* (рис. 3.6). Отже, всі інтегральні криві, що знаходяться на деякій відстані від положення рівноваги, прямують до нього при зростанні часу і. Очевидно, що йдеться про ситуа- цію, коли положення рівноваги є стійким.

Рис. 3.6. Стійке положення рівноваги
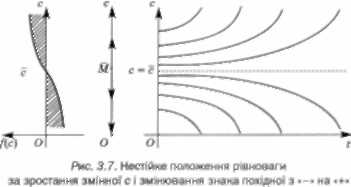
2. Нехай в околі положення рівноваги с* похідна Де)
змінює знак «-* на «+» при зростанні змінної с. Тоді
_ ■ Лса Л
при с„<с маємо —- < 0 , а це означає, що всі значення
с„, розміщені нижче прямої с = с\ зменшуються, тобто віддаляються від положення рівноваги с = с*. При сп > с
маємо > 0, а це означає, що всі значення с_, розмі- рі
щені вище від прямої с = с, збільшуються, тобто теж віддаляються від положення рівноваги с = с (рис. 3.7). У цьому разі очевидно, що положення рівноваги не- стійке.
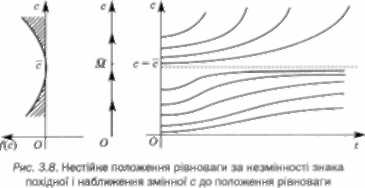
3. Якщо в околі точки с* похідна /(с) не змінює знака, то з одного боку від положення рівноваги с ■ с* значення с„ віддаляються від с', а з іншого від прямої с = с' значення сп наближаються до с* і навпаки (рис. 3.8 і 3.9). Отже, положення рівноваги є нестій- кими.
|
|
і |
|
|
г |
\ |
^^^^ |
с |
и і 1 |
с - с |
|
|
|
1 |
|
№ 0 |
о |
0 |
|
Рис. 3.9. Нестійке положення рівноваги за незмінності знака похідної і віддалення змінної с від положення рівноваги
Для дослідження стійкості положення рівноваги системи з двох і більше диференціальних рівнянь розро- блений спеціальний метод (О. Ляпунов).
Динамічні системи, що описуються системами зви- чайних диференціальних рівнянь типу ,3.2.1), (3.2.2) або ,3.2.3), називають точковими системами, або точ- ковими моделями. В усіх точках простору для такої системи значення концентрації однієї і тієї самої речо- вини ,або щільності популяції) однакові в кожен момент часу. Більш загальними є моделі, що описують зміну концентрації речовини не тільки в часі, а й у про- сторі, коли на розподіл речовин впливають дифузійні або інші процеси.
