7.1. Загальний вигляд математичної моделі динамічної системи з розподіленими характеристиками
Позначимо с(х, у, г, І) концентрацію речовини, що розповсюджується в просторі, або концентрацію (густи- ну) біомаси організмів, популяцій, угруповань. Змінна с(х, у, г, і) може також позначати кількість організмів певного виду популяції або угруповання.
Загальну математичну модель динаміки розподілу у просторі (або екосистемі) у'-ї (у = 1, 2, л) речовини (організмів у-го виду) описує диференціальне рівняння у частинних похідних:
де, (с?с} 6*е. ЛЛ
де Ух, У¥, Уг — складові швидкості переміщення середо- вища (наприклад, повітря або води), в якому перебуває досліджувана речовина (організми).
Якщо система (7.1.1) не автономна, її постійні пара- метри (коефіцієнти) стають змінними і залежними від часу, а простір може містити джерела та стоки із зміню- ваною у часі інтенсивністю.
Систему рівнянь: де,
-£ = Рі{сї,сл.....са,1), де / = 1,2.....п , (7.1.2)
називають точковою моделлю, що відповідає моделі з розподіленими параметрами (7.1.1). Функція І*\(с,, с2, ...» са, х, у, г, І) у загальному випадку може бути нелі- нійною або лінійною зі змінними коефіцієнтами, залеж- ними від часу і.
7.2. Побудова моделей масопереносу в нерухомому та рухомому середовищах
Виділимо в середовищі, яке розглядаємо, елемен- тарний (малий) простір у вигляді куба (або паралелепі- педа) з паралельними осям координат ребрами довжи- ною Ах, Ау, Аг (рис. 7.1).
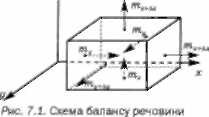
Позначимо кількість речовини, що дифундує через одиничну площину за одиницю часу в напрямку осі
абсцис (Ох), через тх, а кількість речовини, яка дифун- дує через такі самі площини у напрямках осі ординат (Оу) та осі аплікат (Ог), — відповідно, через т„ і тг. Тоді закон Фіна можна записати в такому вигляді:
тж=_2)|£, ттг=-В^-, (7.2.1) дх * ду дг
де с(х, у, г, І) — концентрація речовини, що розповсю- джується шляхом дифузії.
Величини тх, ту, тг називають густиною потоку речовини (організмів), що дифундує, а величину £> — коефіцієнтом молекулярної дифузії (коефіцієнтом дифузії).
Якщо речовина (мікроорганізми) розповсюджується в рухомому середовищі, швидкість якого У(У„ Уу, Уг), то виконується т. зв. узагальнювальний закон Фіка:
т'=сУ'' ° І • п>= сУ«' ° % •т-= сУ-_ ° І •(722)
де У,, У¥, У, — складові вектора швидкості руху середо- вища (повітря, води).
Складемо баланс дифундуючої речовини, що надхо- дить в елементарний куб (паралелепіпед) і виходить з нього (рис. 7.1). Кількість речовини, одо надходить у куб через ліву грань за час АІ, дорівнює:
т,АуАгАІ. (7.2.3)
Кількість речовини, що виходить з елементарного куба через праву грань за час АІ, дорівнює:
т^^уАгАї. (7.2.4)
Отже, при розповсюдженні речовини в напрямку осі абсцис в елементарному кубі накопичується така кіль- кість речовини:
тхГйхАуАгАІ - т^уАгАІ = (т,, д, - тх)АуАгАі. (7.2.5)
Скориставшись формулою Лагранжа:
І(х + Ах) - *\х) = /'(с)Ах, дех<с<х + Ах, (7.2.6)
вираз (7.2.5) перепишемо у такому вигляді (знак мінус перед похідною означає, що накопичення речовини в кубі відбувається за спадної функції тх):
-^-АхАуАгАі. (7.2.7) <Іх
Аналогічні вирази одержимо при підрахунку кіль- кості речовини, що накопичується в елементарному кубі при її розповсюдженні в напрямках осі Оу та осі Ог:
--^-АхАуАгАі, -^дяд^дгдї. (7.2.8)
Склавши вирази (7.2.7) і (7.2.8), обчислимо масу речовини, що накопичується в елементарному кубі об'є- мом &\У = АхАуАг за час Аі, тобто одержимо рівняння балансу (збереження маси) речовини, що дифундує:
Ш = -^ШАІ-^ША,-^ШМ. (7.2.9)
дх ду дг
Розділивши ліву і праву частини рівняння на ДИ'Дї і переходячи до границі при Аі —> 0 (ДМ —> 0), одержимо:
дс=_дт^_^К (7210) ді дх ду дг
У лівій частині рівняння (7.2.10) враховано, що
\М
АС =-.
А\¥
Із рівнянь (7.2.1) та (7.2.10) отримаємо рівняння, що описує розповсюдження речовини в нерухомому середо- вищі (рівняння молекулярної дифузії):
'д2с д2с ©V
ді
дх2 ду2 дг2
(7.2.11)
а з рівнянь (7.2.2) і (7.2.10) — рівняння, що описує роз- повсюдження речовини в рухомому середовищі (рівнян- ня конвективної дифузії):
д2с
дх ду * дг
Якщо в процесі розповсюдження речовини настала
де
рівновага — = 0, то з рівнянь (7.2.11) та (7.2.12) одер-
ді
жимо рівняння стаціонарного розподілу у просторі
дифундуючої речовини, відповідно, в нерухомому та рухомому середовищах:
д с д с д с л . - і.,.
^ГТ + ТТ + ТТ = 0' (7.2.13)
дх2 ду2 дгг
І)
дг2
оу2
дх ду " дг
(7.2.14)
Рівняння (7.2.13) називають рівнянням Лапласа і описують ним багато різних фізичних стаціонарних процесів (дифузію, теплопровідність тощо).
Якщо в області розповсюдження речовини О існують джерела цієї речовини або відбувається її розклад (хімічні або біологічні перетворення, описані функцією Р(с, х, у, 2, і)), то рівняння (7.2.11) і (7.2.12) набудуть, відповідно, вигляду:
(7.2.15)
ос „, _| а2с д*с д'с
^Щс,х,у,г,І) + В&е-У,^-У,^-У.^. (7.2.16)
Перейдемо в рівнянні стаціонарної конвективної дифу- зії у разі відсутніх джерел і хімічних (біологічних) пере- творень (7.2.14) до безрозмірних величин. Розділивши
його на У (V = ^У2 + V* + V2) і помноживши на Ь2 (Ь —
характерний розмір області розповсюдження речовини С), одержимо:
Ь*\п(&е д*с #с
_К —-V —-У —
х дх "ду 'дг
= 0
або
- Ь
|
|
д'с |
д2с |
У |
ІЇІ |
•В |
ЧіГ. |
|
де |
уу де |
Уг де |
"<!) |
"•{£ |
|
|
= 0.(7.2.17)
Позначивши безрозмірну швидкість і безрозмірні
V V V
(приведені) координати: К=-7Г* К = ~Ї7' ***=17'
X Хі я
х' = —, у' = —, г' = —, рівняння (7.2.17) перепишемо
ь ь ь
у вигляді:
П V
д2е
д{х)г 8(у)2 Ь\гУ
-ь[у;^-у;^-у;^)--о. <7.2лв>
\ дх ¥ ду дг ) Рівняння (7.2.18) можна переписати в такому вигляді:
Ь^е &с
д{х)£ д(у)2 д{г)
д2с
•\2
ЬУ „. де
г. де
. де"
В * дх' ду дг\
- V' — - V —
= 0. (7.2.19)
Величину називають числом Пекле і позначають
так:
Ре =
В
(7.2.20)
Із рівняння (7.2.19) видно: якщо Ре < 1, то перева- жає молекулярний перенос, що утворюється внаслідок неоднорідності концентрації речовини в просторі й опи- сується рівнянням Лапласа:
Л Л % = 0, (7.2.21)
дх2 ду2
дг
Якщо Ре > 1, то переважає конвективний перенос, що утворюється внаслідок руху середовища зі швидкі- стю V і описується рівнянням у частинних похідних першого порядку:
,.дс_
я дх
-У.
.де „.де
-У
дг
= 0,
(7.2.22)
де складові (компоненти) швидкості руху середовища У,, У'у, У: визначаються за допомогою натурних спостережень або спеціально розробленої гідродинамічної моделі.