3.7. Моделювання динаміки риб і їх паразитів в умовах токсичного забруднення водного середовища

Актуальність проблеми моделювання процесу захворювання популяції риб

Звичайні біологічні дослідження природних попу- ляцій риб та їх паразитів не охоплюють екологічно най- важливіших паразито-хазяїнних взаємовідносин, на які значний вплив має стан навколишнього водного середовища (довкілля), вивчаючи лише окремі етапи їх життєвого циклу. Для наукового обгрунтування досто- вірності цих біологічних та екологічних досліджень необхідно застосовувати сучасні методи обробки

інформації. Проте для вивчення гідробіонтів на популя- ційному і біоценотичному рівнях, коли основну увагу спрямовано на дослідження динаміки відносин і при- чинно-наслідкові зв'язки між популяціями, засто- сування лише методів біометрії недостатньо. У цьому випадку потрібно застосовувати методи математичного моделювання, враховуючи залежність життєвого циклу системи «паразит — хазяїн» від основних параметрів водного середовища, зокрема якості води. Важливим аспектом гідропаразитологічних досліджень є вплив токсичного забруднення водного середовища на зміни видового складу паразитофауни риб, кількісні характе- ристики паразитарних інвазій, структуру гідропарази- тоценозів та інші показники популяцій паразитів.

З огляду на недостатність і неоднорідність емпірич- ного матеріалу, що характеризує перебудову структур- но-функціональних особливостей організації паразито- цеиозів риб в умовах токсичного забруднення води, для розроблення конкретної математичної моделі доцільно застосовувати методологію побудови математичних моделей при відносинах типу «хижак — жертва». При цьому слід враховувати, що система «паразит — хазяїн», як і «хижак — жертва», досить динамічна, тобто шанси на виживання, збереження гомеостазу та репродукційні можливості у ній постійно змінюються або на користь «хазяїна», або «паразита». «Паразит» викликає у «хазяїна» певний патологічний стан, унаслідок якого можливе зниження темпів росту (розмноження) та репродукційних можливостей. За значного потенціалу опору (резистентності) «хазяїна» продуктивність істот- но не зміниться, тобто система може стабілізуватись. У протилежному разі «хазяїн» гине або патологія перехо- дить у стійку хронічну стадію з летальним кінцем, часто разом з інвазуючнми її паразитами. Якщо життєз- датність «хазяїна» підтримують зовнішніми засобами, наприклад за допомогою лікувальних препаратів або профілактичних заходів, то динамічна рівновага зміщу- ється у бік «хазяїна», а «паразит» гине або його пато- генність стрімко знижується.

Математичне моделювання дає змогу оцінити зміни в структурі і чисельності системи «паразит — хазяїн» у разі токсичного забруднення водного середовища, а в окремих випадках — визначити умови стійкості дина- мічної системи.

Побудова простих моделей

Математичні моделі системи «паразит — хазяїн» суттєво посприяли розвитку досліджень у галузі еколо- гії паразитів із застосуванням математичного апарату і кількісних методів. За допомогою цих моделей було вивчено окремі аспекти функціонування системи «паразит — хазяїн» у водному середовищі. Однак не враховували виливу антропогенних факторів, зокрема токсикантів.

Сучасні моделі системи «паразит — хазяїн» врахо- вують процеси народження, смертності, плодовитості, міграції і розподілу популяцій паразитів в умовах ток- сичного забруднення водного середовища. Розглянемо найпростіші лінійні моделі, що складаються з одного або двох диференціальних рівнянь. Якщо припустити, що популяція паразитів чисельністю Р перебуває в досить сприятливих умовах усередині «хазяїна» (риби), то динаміку популяції паразитів можна описати рів- нянням типу (3.3.3), а саме:

— = аЕ0-тР, а>0, (3.7.1)

де а — стала швидкості імміграції яєць паразитів в організм риби («хазяїна»); Е0 — кількість яєць парази- тів у водному середовищі; т — коефіцієнт природної смертності паразита (т > 0).

За несприятливих умов перебування популяції пара- зитів (при виділенні токсинів в організмі «хазяїна» або токсичному забрудненні зовнішнього середовища (води)) розмноження популяції паразитів уповільниться, а в деяких випадках зупиняється. Коли виділяються токси- ни в організмі «хазяїна», збільшується природна смерт- ність паразитів, тобто новий коефіцієнт смертності т буде більший, ніж попередній т (т* > т). За токсично- го забруднення водного середовища зменшується кіль- кість іммігруючих яєць паразита, оскільки в токсично- му водному середовищі частина яєць загине, а отже, зменшиться стала швидкості імміграції а (а < а).

Нехай у певний час і = і0 = 0 спостерігалась чисель- ність паразитів Р„. Тоді, розв'язавши рівняння (3.7.1, з урахуванням початкової умови

Р(10) - Р(0, - Р0, (3.7.2,

для знаходження чисельності популяції паразитів за сприятливих умов у будь-який час одержимо формулу:

р(г, = 2& + (р0 - 5& Vй'. (3.7.3)

т \ пг )

У разі несприятливого стану навколишнього середо- вища чисельність паразитів визначають за рівністю:

Р'(і) = ^ + (р0 ~ ^)ет''. (3.7.4)

Із співвідношень (3.7.3) і (3.7.4) випливає, що за значний відрізок часу (( -* оо) чисельність паразитів в умовах як чистого, так і токсично забрудненого водного середовища прямує до стійкого (рівноважного) стану і визначається, відповідно, такими величинами:

р„ = ^, р; = 4я„, (3-7.6)

пг т

причому

т т

Отже, при токсичному забрудненні чисельність

а'Е0

паразитів зменшується і прямує до величини —~ .

т

Вплив зменшення чисельності паразитів на динамі- ку чисельності популяції «хазяїна» ілюструє модель, розроблена з урахуванням взаємодії між популяціями паразита і «хазяїна». Якщо позначити чисельність або біомасу паразита через і\а «хазяїна» — черезН,то най- простіша модель системи «паразит — хазяїн» матиме такий вигляд:

^- = <хЕ0-тР , (3.7.6) Аі

— = гН-$Р, г = Ь-А, (3.7.7) Аі

де г — коефіцієнт розмноження популяції «хазяїна»; Ь — коефіцієнт народжуваності (Ь > 0); А — коефіцієнт смертності (А > 0); р — коефіцієнт шкідливої дії (приг- нічення) паразита щодо «хазяїна».

Стаціонарний (стійкий, або рівноважний) розв'язок системи (3.7.6)—(3.7.7) має вигляд:

т

тг

(3.7.8)

Нестаціонарні розв'язки системи (3.7.6)—(3.7.7) знаходять так само, як і системи (3.5.15)—(3.5.16):

Р(і) = к1Е0 + (Р0-к1Е0)е Н(і) = А,А2К0 -

+ Н0 кік2Е0 к2

1 + Ьа 1 +

де введено такі позначення: а

*і =

*з = ^ г

(3.7.9)

(3.7.10)

(3.7.11)

т г

Отримані розв'язки свідчать, що поведінка популя- цій паразитів і риб («хазяїна») залежить від їх початко- вої чисельності Р0 і Н0, а також від параметрів к1г к2, к3. Ці параметри, які визначаються коефіцієнтами швид- кості імміграції, народжуваності, смертності і пригні- ченості, впливають на динаміку популяцій риб та їх паразитів (рис. 3.26).

Р. н

р?

(г>0)

Р.Н к,Е0

" — (г < 0)

.........«-.«-ї-заоввв-

Рис. 3.26. Графіки сценаріів розвитку популяцій в системі -паразит — хазяїн-

Отже, навіть порівняно проста математична модель описує досить різні й цікаві випадки (сценарії) динамі- ки чисельності популяцій риб та їх паразитів за умов токсичного забруднення водного середовища, яке викликає зміну параметрів А1( А2, А3.

Побудова складних моделей

Проста математична модель (3.7.6)—(3.7.7) описує односторонній вплив паразита на «хазяїна». За допомо- гою моделей зі зворотними зв'язками можна описати процеси саморегулювання. Крім того, у простих моделях обумовлено, що чисельність яєць паразитів є сталою величиною (Е0 = сопзгу). Проте кількість яєць у водному середовищі істотно залежить від кількості дорослих паразитів в організмі «хазяїна», а також від кількості яєць, що гинуть внаслідок їх поїдання та природної смертності (її рівень підвищується зі збільшенням інтенсивності токсичного забруднення). Динаміка чисельності яєць паразитів була вперше описана в моде- лі системи «паразит — хазяїн» (Р. М. Андерсен), у якій враховано зворотний зв'язок при імміграції личинок паразитів. Зважаючи на викладене, запишемо лінійну модель системи «паразит — хазяїн» з рівнянням дина- міки яєць у водному середовищі:

— = аЕ-тР , (3.7.12) Аі

— = гН-$Р, г^Ь-Л, (3.7.13) аі

^ = аР - а,£ - у#\ аї=а + т1, (3.7.14)

де: а — коефіцієнт інтенсивності появи яєць паразитів у водному середовищі; Е — кількість яєць паразитів у водному середовищі; у — коефіцієнт поїдання яєць; Н* — кількість водних організмів, що знищують яйця паразитів Н' = В + УоН (В — кількість водних організ- мів, які не досліджуються); т, — коефіцієнт природної смертності яєць паразитів; а, — коефіцієнт смертності яєць паразитів з урахуванням імміграції в організм «хазяїна».

При підвищенні інтенсивності забруднення водного середовища токсикантами значно збільшаться коефіці- єнти а! і у та зменшаться коефіцієнти а і г.

Модель (3.7.12)—(3.7.14) враховує взаємовплив дорослих паразитів та їх яєць (личинок), але не врахо- вує впливу чисельності популяцій «хазяїна» на чисель- ність паразитів. Тому крім наведених вище моделей

доцільно розглянути кілька модифікованих лінійних моделей з додатковими зворотними зв'язками.

Враховуючи взаємний вплив паразита і «хазяїна» за постійної кількості яєць Е0, одержимо модель із саморе- гуляцією:

^ = аЕ0 - тР + р,Я, (3.7.15)

йі

= гЯ-р2Р

(3-7.16)

де і Рг — сталі взаємного впливу «хазяїна» на парази- та і паразита на «хазяїна». Якщо припустити, що вплив токсичного середовища змінюється в часі від наймен- шої інтенсивності Ктіп до найбільшої Ктах для паразита і від К'ти, до для «хазяїна», то відповідна математич- на модель матиме вигляд системи диференціальних рів- нянь зі змінними коефіцієнтами (неавтономна система):

аі

ан аі

= гЯ-р\

)е"*]я, (3.7.17) }Р, (3.7.18)

де А і А* — сталі верифікації; р,. = — — стала інтенсив-

ну; — с

ності дії токсиканта; скр — гранична (критична) концен- трація токсиканта у воді, за якої гине понад 50% пара- зитів і «хазяїв»; с — концентрація токсина у воді; р, і Рг — коефіцієнти інтенсивності взаємодії між «хазяї- ном» і паразитом.

Узагальнення лінійної моделі (3.7.17)—(3.7.18) дає змогу побудувати нелінійну модель і записати її в тако- му вигляді:

*£

Р,

ар

аі

= аЕ- тР'

аі

к'і

РН, (3.7.19)

ЯР. (3.7.20)

Щоб урахувати умови розвитку яєць паразитів та їх вплив на динаміку системи «паразит — хазяїн», достатньо

до систем рівнянь (3.7.15)—(3.7.16,, (3.7.17)—(3.7.18) або (3.7.19)—(3.7.20) додати лінійне рівняння (3.7.14) або нелінійне рівняння:

= аРН -О.Е- пцЕ2 - уН'. (3.7.21)

Система рівнянь (3.7.19)—(3.7.21) є достатньо пов- ною і враховує основні фактори впливу на динаміку «хазяїв» (риб), паразитів та їх яєць (личинок)у водному середовищі.

Урахування навіть досить простих відносин між популяціями «хазяїв» (риб), популяціями паразитів (гельмінтів, цестодозів та ін.) та їхніми яйцями (личин- ками) при застосуванні математичних методів призво- дить до складних, у т. ч. нелінійних, моделей, які опису- ють нелінійними диференціальними рівняннями. Водно- час використовуючи прості і складні математичні моделі для проведення імітаційного експерименту, можна вибра- ти практично ефективну модель, яка після верифікації дасть змогу розв'язати важливі екологічні питання під час дослідження системи «паразит — хазяїн».

3.8. Кількісна оцінка

екологічної ємності

і самоочисної здатності біосфери

Одним із найважливіших завдань сучасної екологіч- ної науки є оцінювання впливу людини на навколишнє середовище (ОВНС) і розроблення ефективної стратегії взаємодії людини з природою, що є необхідним для функ- ціонування всіх елементів біосфери, в т. ч. самої людини. Інакше кажучи, реалізація відповідних заходів має забезпечувати рівновагу, сталість і гнучкість природних систем, порушення яких може призвести до ненередба- чувалих негативних наслідків і екологічних катастроф.

Проблеми стійкості, рівноваги, гомеостазу екосисте- ми та біосфери є центральними в сучасній екології. Дос- лідження у цій галузі мають спиратися на закони розвитку біосфери, основні принципи і закони еволюції людини та біосфери, їхню взаємозалежність в еволю-

цінному розвитку. Згідно з цими законами причинами екологічної кризи є непродумані дії людини, внаслідок яких не лише гинуть біологічні види, а й руйнується здатність природних систем і комплексів до відновлен- ня І саморегуляції, більше того — система саморегуля- ції починає вдіяти» проти людства.

Розв'язання центральних екологічних проблем і розвиток основних положень теорії стійкості й гомеос- тазу екологічних систем стимулюють подальші дослі- дження фундаментальних екологічних понять, які сприяють глибшому розумінню механізмів еволюцій- них перетворень у природі та взаємозв'язків людини з навколишнім природним середовищем.

Основну властивість біосфери та її екосистем — здат- ність до адаптації в сучасних умовах інтенсивного антропогенного впливу і забруднення навколишнього середовища — відображає поняття «екологічна ємність природної системи» (екосистеми, ландшафту, біому, біосфери). Сучасна література з екології по-різному тлу- мачить і визначає поняття «ємність», а саме: кількість забруднювальних речовин, які приймає водойма без збіль- шення їхньої концентрації до рівня, що спричинює деформацію екосистеми і є неприйнятним для людини т. зв. «приймальна ємність водойми» (А. Константи- нов); «ємність геофізична», яка визначається за швид- кістю седиментації; «геохімічна ємність», зумовлена хімічними перетвореннями; «біологічна ємність», що залежить від темпу біоседиментації та біодетоксикації забруднень; «радіоємність», «кондиціонуюча ємність». Однак кожне із визначень розкриває лише частину ознак і властивостей, які відображають здатність екоси- стем, а отже, і біосфери, до самозбереження, саморегу- лювання і самовідновлення. Це фундаментальне еколо- гічне поняття пов'язане з проблемами стійкості й рівно- ваги екосистеми. Перед екологами постає важливе і складне питання: як і наскільки можуть бути змінені абіотичні умови, умови розвитку окремих видів і угру- повань рослинного і тваринного світів, щоб не було порушено стійкості екосистем. Незважаючи на достат- ню гнучкість (еластичність) екосистем, в одних випад- ках їх стійкість може не порушуватися при порівняно великих навантаженнях (змінах) навколишнього сере- довища (наприклад, середовища життя гідробіонтів), а

її інших — екосистеми не витримують порівняно неве- ликих антропогенних впливів. Очевидно, йдеться про велику і досить обмежену екологічну ємність екоси- стеми.

Екологічна ємність екосистеми — максимальна кількість енергії або речовини, яка може бути залученаекосистемою в колообіг за одиницю часу без істотних порушень її структури і стійкого функ- ціонування.

В основу визначення ємності екосистеми покладено речовинно-енергетичний підхід, у межах якого функ- ціонування екосистем розглядають як процес трансфор- мування енергії й речовин, які надходять із навколиш- нього середовища і повертаються у те саме навколишнє середовище. У процесі трансформації енергія і речови- ни переходять у форми, які забезпечують безперервний потік колообігу речовини в екосистемі, його рівновагу і усталений баланс речовини й енергії в біосфері. Такий колообіг є необхідним для підтримання стійкого функ- ціонування структур і зв'язків, що сформувалися в еко- системі. Види енергії й речовини, не здатні трансформо- вуватися в прийнятні для екосистеми форми, не будуть втягнуті в біологічний колообіг. Накопичуючись на певній ділянці складного шляху, на якому відбувається колообіг, вони можуть порушити усталений баланс речовин між біологічною системою і абіотичним навко- лишнім середовищем. Це може призвести до суттєвої зміни середовища проживання організмів, а отже, до зміни функціонування екосистеми і порушення стану її динамічної рівноваги. Якщо процес стане необоротним, екологічна стійкість системи буде порушена.

Отясе, екологічна ємність визначає (характеризує) можливість екосистеми перетворювати енергію і речо- вину, які надходять у неї, на форми, що здійснюють біо- логічний колообіг, проходячи в екосистемі історично сформований особливий шлях. Зокрема, такому коло- обігові сприяє послідовний перехід багатьох речовин із неорганічних форм в органічні і навпаки. Так, екоси- стема перебуватиме в стійкому динамічному стані, якщо притік біогенних елементів у систему врівноваже- ний їхнім відтоком із цієї системи і переходом в іншу суміжну екосистему. Екологічна ємність характеризує потужність екосистеми, в якій трансформуються, мігру- ють і накопичуються речовин, які здійснюють круго-

обіг, тобто вона визначає потенційні кількості речови- ни й енергії, що можуть бути втягнуті екосистемою в колообіг. Поняття «екологічна ємність» дає змогу от- римати (визначити) науково обґрунтовану кількісну оцінку впливів, які можуть порушити стійкість еколо- гічних систем. Визначення для екосистеми максималь- но допустимих навантажень (МДН) є найважливішим і досить складним завданням під час екологічного оціню- вання антропогенного виливу на екосистеми і безпосе- редньо стосується проблеми стійкості екосистем і біо- сфери загалом.

Нехай буде відома реальна кількість т) і-'і речовини (або енергії), яку екосистема втягує в колообіг за оди- ницю часу. Тоді, якщо екологічну ємність характеризу- вати величиною е(, легко визначити величину екологіч- ного резерву гу:

г, = егтг (3.8.1)

Якщо відомо величини і пг/ для Л' різних речовин, які беруть участь у колообігу, то величину сумарного (загального) екологічного резерву К визначають рівнян- ням:

Д-Е-М-=|>. • (3.8.2) /-і /-і і-і

Для того щоб практично визначити кількісні харак- теристики екологічної ємності й екологічного резерву досліджуваних екосистем і ландшафтів, необхідно врахувати здатність екосистем до гнучкості і стійкості, яка виявляється, зокрема, в самоочищенні. Здатність до самоочищення пов'язана з можливістю екосистем втягувати в колообіг дещо більшу кількість речовини, ніж та, яку вони втягували до антропогенних впливів.

Тому зайві кількості речовин, які надходять до еко- системи, можуть частково вводитись у колообіг, не за- бруднюючи навколишнього середовища, а отже, не порушуючи необхідного балансу речовин в екосистемі. Особливо зручно визначати самоочисну здатність вод- них екосистем — сукупність природних гідрологічних, хімічних і біологічних процесів, що відбуваються в заб- руднених водних об'єктах та спрямовані на відновлен- ня початкових властивостей і складу води. Отже, понят- тя «самоочисна здатність» тісно пов'язане з поняттями

«екологічнаємність», «стійкість», «рівновага» й «гнуч- кість» екосистем.

Використовуючи поняття «самоочисна здатність» і методи імітаційного математичного моделювання, можна кількісно охарактеризувати самоочисну здатність, а отже, оцінити екологічну ємність і екологічний резерв різних екосистем.

Самоочищення водних систем (річок, водосховищ, озер та ін.) зумовлює багато природних, а іноді і техно- генних факторів: гідрологічні, гідрохімічні й гідробіо- логічні процеси, зокрема розведення і водообмін; седи- ментація завислих частинок і скаламучування донних відкладів; хімічне перетворення речовини; біологічна трансформація органічних і неорганічних речовин; радіоактивний розпад. Здебільшого самоочисну здат- ність водної системи або водного об'єкта визначають за зміною концентрації речовини, яка надходить до двох або більше створів. Крім того, один створ розміщують вище від джерела забруднення (фоновий створ). У цьому разі самоочисну здатність (СЗ) водного об'єкта на його і-й ділянці відносно у-ї забруднювальної речови- ни обчислюють за допомогою формулами:

С3= 4 , Ч —, (3.8.3) (СГ*"+С^')АТі/

де Со 2-' — концентрація у-ї речовини в незабрудненому потоці (у фоновому створі); С{ ~ *•' — концентрація у-ї речовини в початковому (вхідному) створі і'-ї ділянки; Стч — концентрація у-ї речовини в кінцевому (вихідно- му) створі даної ділянки через час Ах = х,, - х1г причому С{ иіа С," 2 Со"**'" >0(СІ~ - Сі'2-' = сопзі).

Для кількісної характеристики сумарної (загальної) самоочисної здатності відносно декількох інгредієнтів (у= 1,2,3, ...,/У) на і-й ділянці водойми використовують формулу:

)=і 14 + гахц (3.8.4)

де сталі аі(}= 1,2,3, ..../У) приписують кожному з додан- ків певну вагу (показник шкідливості у'-'ї речовини).

Чим більша обчислена за формулами (3.8.3) або (3.8.4) величина СЗ г, тим вищою є здатність водної еко- системи до опору Й адаптації, її стійкість до впливу

негативних факторів, передусім забруднення водного середовища різними речовинами.

Отже, самоочисна здатність природної системи ха- рактеризує її екологічну ємність (ЕЄ), яку визначають як показник максимальної кількості енергії й речови- ни, втягненої екосистемою в колообіг без істотних пору- шень (змін) її структури й функціональних особливо- стей. Однак якщо за допомогою екологічної ємності характеризують потенціальну здатність екосистеми до адаптації і стійкості лід час антропогенних впливів, то самоочисна здатність є наслідком цієї можливості і характеризує результати функціонування екосистеми в певних конкретних умовах. Ці поняття характеризують екосистему лише на певній ділянці простору (ландшаф- ту), який вона займає, і тільки в певний проміжок часу.

Визначення кількісних характеристик екологічної ємності, зокрема вимірювання потоків енергії і речови- ни, що здійснюють колообіг в екосистемі, пов'язане із значними методичними труднощами. Встановлення кількісних показників самоочисної здатності екосисте- ми є нескладним, оскільки відомі концентрації різних інгредієнтів на вході й виході досліджуваної системи. Отже, СЗ є важливою і ефективною кількісною характе- ристикою ЕЄ природної системи.

Розглянемо одну з можливих математичних моделей, яка описує процеси самоочищення водойм і водотоків. Завдання полягає в тому, щоб скласти таке математичне рівняння, яке із застосуванням розрахункового методу допоможе визначити концентрацію на виході системи, при заданій концентрації на вході з урахуванням усіх основних факторів впливу на процеси самоочищення.

На процеси трансформації, міграції і накопичення речовин, які забруднюють воду, а отже, на самоочисну здатність водойм найбільше впливають такі фактори:

— річний стік, водообмін і динаміка водних мас;

— випаровування і опади;

— бічний притік, дренажний стік й інфільтрація підземних вод;

— промислові і побутові стоки;

— безповоротне водоспоживання;

— седиментація завислих частинок і скаламучуван- ня донних відкладів;

— сорбція, десорбцій та інші фізико-хімічні пере- творення;

— біохімічні процеси, пов'язані з продукуванням і деструкцією фіто- й зоопланктону;

— процеси взаємодії з вищими водними рослинами та іншими гідробіонтами (асиміляція біогенів. поглинання і накопичення речовин безхребетними та іхтіофауною);

— радіоактивний розпад.

У різних водних системах вони діють неоднаково. Самоочисна здатність водного об'єкта залежить від різ- номанітності й інтенсивності факторів впливу. Багато з них є, як правило, стабільними характеристиками, вла- стивими певній річці, водосховищу, басейнові річки, площі водозбору, ландшафтові. Антропогенний вплив на природу спричинює зміни більшості наявних факто- рів самоочищення і появу нових. Наприклад, під час зарегульовування річок і утворення водосховищ суттє- во збільшується екологічна ємність річок.

За допомогою імітаційної математичної моделі можна визначити самоочисну здатність річки до і після її зарегульовування і оцінити зміну екологічної ситуа- ції (екологічної ємності) при утворенні водосховищ і збільшенні антропогенного навантаження. Використо- вуючи математичне моделювання, можна також зміню- вати антропогенне навантаження в досить широких Інтервалах і оцінити реакцію екологічної системи на це навантаження. Оцінку реакції одержують, визначивши концентрацію С речовин, які забруднюють воду (орга- нічних і неорганічних речовин, хімічних і радіоактив- них елементів тощо).

Застосовуючи балансові методи, відомі закони збере- ження речовини і кінетичні рівняння, концентрацію у-го інгредієнта на їй ділянці річки (водосховища) виз- начають за допомогою диференціальних рівнянь:

" * + ^ + де -

аі

-у'/<[^т.х+ (1- Й«)е- ^РІЩУР. (3.8.5)

1

з:

(3.8.6)

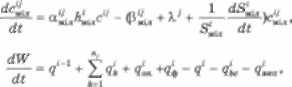
(3.8.7)

(3.8.8)

де: а1, с1' — загальна витрата води в річці (водосховищі) на і-й ділянці і концентрація у воді у-го інгредієнта (речовини) на цій ділянці; IV' — об'єм води на і-Й ділян- ці річки (водосховища); д'~1, с*~',у — витрата води і кон- центрація в ній у-го Інгредієнта на і-й ділянці річки (водосховища); а],, сЦ — витрата води к-го водотоку (при- току) і концентрація в ньому у-го інгредієнта; а^, с|' — підземний стік (фільтраційна витрата) і концентрація в ньому у'-го інгредієнта; а'оп, сЦа— кількість (потік) опадів і концентрація в них у'-ї речовини; о'^, с'аяа — величини водоспоживання і випаровування; д^я, сЦіл — концентра- ція у-ї речовини в донних відкладах глибоководних і мілководних ділянок водосховища; а'^, — сталі швидкості седиментації і скаламучування на глибоко- водних ділянках водосховища; а^,, Р&я — сталі швид- кості седиментації і скаламучування на мілководних ділянках водосховища; З'г'„, — площі глибоководних і мілководних ділянок; л'гл, ^,ія — середні глибини гли- боководних і мілководних ділянок; X', у'/, 8',', К$ — сталі радіоактивного розпаду й швидкості трансформації у-ї речовини; Ф\' — числова характеристика 1-го фактора, який впливає на самоочисну здатність унаслідок гідро- хімічних і гідробіологічних процесів; І — час у добах (місяцях).

Параметри й змінні величини рівнянь (3.8.5)— (3.8.8) із достатньою для практичних екологічних дос- ліджень точністю описують основні характеристики річкової екосистеми в процесі її функціонування, зміни і перетворення на екосистему водосховища. Для число- вої реалізації моделі необхідно надати конкретного вигляду останньому членові рівняння (3.8.5), який опи- сує гідрохімічні, біологічні і гідробіологічні перетворен- ня. Однак одним із найістотніших факторів, що впливає

на ці процеси, є швидкість Уі потоку водних мас у річці (водосховищі). Самоочисна здатність різко зростає при збільшенні швидкості течії, але до певної межі, а найпо- мітніше впливає на інтенсивність процесу самоочищен- ня збільшення швидкості течії від 0 до 0,2 м/с.

У цьому діапазоні зміни швидкості течії для рівнин- них річок, зокрема дніпровських водосховищ, встано- влено емпіричну залежність відношення динамічної складової коефіцієнта самоочищення К\л - - К'0 до коефіцієнта самоочищення К'0 у стоячій воді від швид- кості течії в річці або водосховищі:

кі-к>_ У'(і)

КІ 0,0031 + 0,0348К'(0 *

З рівняння (3.8.9) в результаті граничного переходу при V, > V визначимо максимальне значення коефіцієн- та динамічного самоочищення К'тиж:

кї-кі = ]іткІ-к<_

я ііш-^-= 28,7. (3.8.10)

0,0031 + 0,0348К'(ї)

Отже, кі

Ктмх = -^- = 29,7 • (3.8.11) К0

Тепер значення коефіцієнта динамічного самоочи- щення можна встановити за допомогою такого рівняння:

КІ = КІ[К'юах + (1 + КІ**)е*"у'], (3.8.12)

де параметр 6'' визначають при верифікації моделі, у якій використано залежність (3.8.12).

Враховуючи співвідношення (3.8.12), визначимо функцію самоочищення Ф' у правій частині рівняння (3.8.5):

Ф'> = у-'К^К^ + (1 + К'тлх)е-""у']с" щ (3.8.13)

де параметр у" дорівнює відношенню часу добігання частинки завислої або розчинної речовини т^, в і-й водоймі до періоду напіврозпаду (окислення) даної речовини т^р. Замість параметра у" можна ввести пара- метр у'', який визначимо як співвідношення швидкостей

5*-5-- <3-8-14>

де К;х — швидкість течії у водосховищі, Ур — швид- кість течії в річці.

Коли необхідно визначити не абсолютне значення концентрації забруднювальної у-ї речовини, а лише зміну концентрації цієї речовини залежно від умов функціону- вання водної екосистеми й динаміки гідрологічних і мор- фометричних параметрів, за величину К'0 можна взяти будь-яке число, наприклад 1 або 10. При з'ясуванні істинного значення концентрації с1' величину К{, встано- влюють у результаті експериментальних досліджень.

Параметр у'' можна також розглядати як величину, обернену до значення приведеної швидкості течії V:

= = (3.8.15,

де У0 — початкове значення швидкості течії в річці (або у водосховищі) на і-й ділянці.

Точніший вираз для параметра у1' можна знайти, якщо подати його у вигляді

у" = т;^-, (3.8.16)

де сталу уо' визначають у результаті натурних дослі- джень. Стала уо' враховує складний і довгий шлях руху частинки речовини залежно від морфометричних осо- бливостей водотоку або водойми, а також час повного розкладу (окислення) забруднювальної речовини.

Як видно з рівняння (3.8.13), інтенсивність процесів гідрохімічного, біохімічного і гідробіологічного пере- творень забруднювальних речовин залежить від багатьох факторів, оцінювання яких є досить складним. Збіль- шення швидкості течії в певному діапазоні зміни швид- костей сприяє перемішуванню водних мас і пришвид- шенню процесів самоочищення і зменшує час перебу- вання частинки забруднювальної речовини на певній ділянці річки або водосховища, а отже, в деяких випад- ках реакції перетворення речовини (окислення, нейтра- лізації тощо) не закінчаться, і тому самоочисна здат- ність на цих ділянках буде знижена. З огляду на великі

маси води і площі водосховищ, на забруднювальну частинку діє більше, ніж у річках, різноманітних фак- торів самоочищення (наприклад, поглинання вищою водною рослинністю). Тому величина параметра у§ для водосховищ завжди буде більшою, ніж для річок. Вод- ночас вираз у квадратних дужках у правій частині рів- няння (3.8.13) для річок набуває більших значень, ніж для водосховищ, де швидкість течії невелика. Отже, сумарний ефект самоочисної здатності можна оцінити тільки на основі математичного моделювання.

За допомогою описаної моделі (3.8.5) було проведено розрахунки зміни концентрації забруднювальної речо- вини в Кременчуцькому водосховищі і на ділянці Дні- пра, де воно утворене. Вивчали ситуації, коли концен- трація забруднювальної речовини у річці і водосховищі у початковий період часу дорівнювала нулю, тобто для чистої води (рис. 3.27), і коли початкова концентрація с0 дорівнювала концентрації речовини с, у воді на вхід- ному створі, тобто для забрудненої води (рис. 3.28). В обох випадках самоочисна здатність водосховища (суцільна лінія) значно вища, ніж відповідної ділянки річки (пунктирна лінія). За допомогою математичного моделювання підтверджено правильність цього виснов- ку і щодо інших ситуацій.

Будь-яка екосистема не є ізольованою елементарною одиницею біосфери. Між екосистемами існують певні взаємозв'язки, які виявляються в обміні енергією і речовиною. Хоча ці зв'язки та обмін у будь-якому разі менш важливі, ніж між компонентами однієї екосисте- ми, їх не можна не враховувати, бо вони істотно вплива- ють на біологічний колообіг речовини і енергії в дослі- джуваній екосистемі і, відповідно, на її стан.

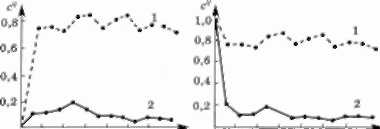
0 50 10О15О200 250 30О * 0 50 100 150 200 250 300 /

Рис. 3.27. Процес забруднення Рис. 3.28. Процес очищення

Розглянемо, наприклад, дві екосистеми: листяний ліс і ставок або озеро, розташовані в лісі або поблизу нього. Восени вітер заносить частину опалого листя у ставок, де воно, розкладаючись, стає їжею для деяких водних організмів. Личинки комах живуть у воді, а дорослі особини залишають водне середовище і оселя- ються в лісі або на сусідніх луках. Отже, між сусідніми екосистемами завжди існують взаємозв'язки, причому їх впливи одна на одну не рівнозначні. В одному разі, очевидно, істотніше впливатиме листяний ліс на ста- вок, а в іншому — ставок на ліс. Інтенсивність односто- роннього впливу однієї із сусідніх екосистем на інші визначається їхнім геоморфологічним положенням у ландшафті і відіграє важливу роль у зв'язку із забруд- ненням навколишнього середовища та антропогенним впливом на екосистеми.

Екосистеми не мають чітких меж, між сусідніми екосистемами існує територія, де їх особливості й характеристики перетинаються.

Екотон — перехідна зона між зовнішньо різними сусідніми екосистемами (біоценозами), яка має більше біорізноманіття порівняно з граничними екосистемами. Так, між лісом і ставком є перехідна зона, де рослини і тварини однієї екосистеми (лісу) постійно зникають і з'являються рослини і тварини другої екосистеми (став- ка). Крім того, види, що адаптувались, роблять екотони важливими для взаємодії сусідніх екосистем, які вони розділяють.

У зв'язку з цим необхідно разом із поняттям «еколо- гічна ємність екосистеми» розглянути сутність поняття «екологічна ємність сусідньої екосистеми», яка істотно впливає на першу, яку називають основною, або базис- ною, а сусідні екосистеми — буферними. Наприклад, базисною екосистемою є ставок (озеро або річка), а буферною щодо ставка — розміщені на площі водозбору ліс або лук. Чим значніша роль буферної екосистеми в здійснюваному базисною екосистемою колообігу речо- вини й енергії, тим більше буферна екосистема вплива- тиме на здатність базисної протистояти антропогенному навантаженню. Інакше кажучи, здатність буферної еко- системи брати на себе частину антропогенного наванта- ження, яке негативно впливає на базисну екосистему,

доцільно пов'язати з поняттям «буферно ємність роз- глядуваної (базисної) екосистеми».

Буферною ємністю базисної (основної) екосистеми називають показник кількості енергії й речовини, які втягуються в біологічний колообіг зо одиницю часу сус- ідніми (буферними) екосистемами. Отже, буферну ємність базисної екосистеми визначає сума екологічних ємностей усіх сусідніх екосистем, що взаємодіють із базисною.

Залежно від розміщення екосистеми в ландшафті і від умов перенесення енергії й речовини в процесі їхньо- го екологічного колообігу розрізняють автономні, тран- зитні й акумулятивні екосистеми, а також проміжні між ними. Буферна ємність автономних екосистем дорівнює нулю. Акумулятивні екосистеми за однакових ландшафтних умов мають більшу буферну ємність, ніж транзитні, які посідають проміжне місце міяс автоном- ними й акумулятивними екосистемами.

Отже, структура розташування різних екосистем на розглянутій ділянці ландшафту або на площі водозбору із розміщеними на ній річками і ділянкою головної річки, яка становить акумулятивну водну екосистему, їхня еко- логічна, а отже, й буферна ємності відіграють важливу роль у підтриманні сприятливої екологічної ситуації як на площі водозбору, так і в басейні малих і великих річок. Оскільки сума екологічних ємностей різних наземних екосистем, розташованих на площі водозбору, визначає буферну ємність водної екосистеми, стан річки і якість води в ній значною мірою залежать від співвідношення різних видів екосистем на площі водозбору.

Розглядаючи схему річкового басейну, доцільно буферну ємність ділянки головної річки розбити на буферну ємність водних екосистем, яка складається із екологічних ємностей приток, і буферну ємність площі водозбору, що складається із екологічних ємностей різ- них видів наземних екосистем. Деякі з наземних екоси- стем басейну впливають на водну екосистему головної річки, яка є базовою акумулятивною екосистемою, через екосистеми приток. Інші екосистеми площі водозбору впливають на базову екосистему безпосередньо.

Імітаційну математичну модель самоочисної здатно- сті водної (наземної) екосистеми можна значно вдоско- налити, доповнивши її рівняннями, що враховують

поняття «буферна ємність». У цьому разі окремі змінні й постійні величини у складі вихідної математичної моделі слід визначати за спеціально складеною систе- мою рівнянь, що описує самоочисну здатність сусідніх (буферних) екосистем.