3.6. Моделювання трофічного ланцюга
Концептуальна модель трофічного ланцюга
У реально існуючих природних екосистемах налічу- ють десятки видів (популяцій, угруповань), що взаємо- діють між собою. Незважаючи на певні математичні труднощі при формалізації складних екосистем і побу- дові математичних моделей взаємодії популяцій, досяг- нуто значних успіхів у питанні математичного моделю- вання популяцій (угруповань), що є ланками єдиного трофічного ланцюга.
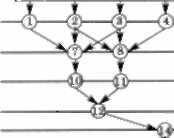
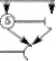
Розглянувши деякий орієнтований граф (схему) озерної екосистеми, вершини якого відповідають ви- дам, включеним до водної екосистеми, а орієнтовані дуги (відрізки) з'єднують види, один із яких є кормом для інших (стрілки на дугах показують шлях руху речо- вини й енергії), легко переконатись, що в структурі цього графа відокремлюються трофічні рівні (рис. 3.22), зокрема: 1, 2, 3, 4 — зелені, синьо-зелені і діато- мові водорості, 5, 6 — зелені водорості (1-й рівень); 7, 8, 9 — рослиноїдний зоопланктон (2-й рівень); 10, 11 — хижий зоопланктон (3-й рівень); 12 — риби, що живляться хижим зоопланктоном, 13 — риби, що живляться рослиноїдним зоопланктоном (4-й рівень); 14 — хижі риби (5-й рівень).
Види, що належать до одного й того самого трофіч- ного рівня, перебувають або в стані конкуренції за кор- мові ресурси (симбіоз), або в коаліції при використанні
цих ресурсів (коменсалізм). і ому представлена на рис. 3.22 трофічна сітка (мережа) відображає взає- мозв'язки тільки між видами різних трофічних рівнів, тобто відтворює тип взаємовідносин «хижак — жертва» («паразит — хазяїн», «споживач — ресурс») і не формує уявлення про взаємодії між видами одного трофічного рівня. У зв'язку із цим виникає необхідність створення математичної моделі таких структур (систем), у яких види послідовно утворюють пари «хижак — жертва». Сформовані цими послідовними парами видів структури (системи) називають трофічними ланцюгами. їх в екоси- стемі може бути кілька. Наприклад, на рис. 3.22 трофіч- ні ланцюги утворюють послідовності видів 1—7—10— 12—14, або 6—9—13—14, або 4—8—11—12—14 і т. д.
Є.
Ям
Ресурс
(сонячне світло та біогенні елементи)
6}— 1-Й рівень
2'й рівень
- 3-й рівень
- -Гй рівень
- 5-й рівень
Рис. 3.22. Схема трофічної мережі
:0
N.
ьлу,
^1 у,.,(*„-,>.
N.
5
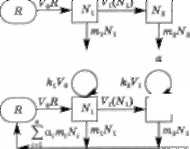
Рис. 3.23. Схема незамкненого(а) і замкненого (б) трофічних ланцюгів
Усі види, що належать до одного й того самого трофіч- ного рівня, можна об'єднати в один псевдовид або виділи- ти з множини можливих ланцюгів т. зв. домінуючий лан- цюг, у якому потік речовини та енергії набагато переви- щує потоки в інших ланцюгах, тобто згорнути трофічну мережу в трофічний ланцюг. У цьому разі трофічну мере- жу агрегованого угруповання описуватиме відповідний незамкнутий або замкнутий трофічний ланцюг (рис. 3.23), у якому на кожному трофічному рівні буде розмі- щений один вид або псевдовид. Наприклад, щодо соняч- ного світла (сонячної радіації) екосистема є незамкне- ною, а стосовно біогенних елементів (вуглець, азот, фос- фор та ін.) екосистеми можуть частково замикатися за рахунок діяльності т. зв. деструкторів (мікроорганізми, гриби, черв'яки), які розкладають органіку до мінераль- них компонентів, що стають кормом для первинного тро- фічного рівня (біогенні елементи).
Математична модель трофічного ланцюга
Використовуючи схему трофічного ланцюга (рис. 3.23) та враховуючи описані раніше математичні моделі, можна записати систему диференціальних рівнянь від- носно біомас різних видів або псевдовидів, що утворю- ють цей трофічний ланцюг:
* = Я0 - той - К0ЛГ, + І І.
: 1-і......і
—1 = ЬіУ0М1-тї^-У1М2, аі
4& = кгУ^2 - щЩ - У2М3 , <3,6Л)
аі
де (?0 — зовнішній потік ресурсу (світло); й — первин- ний ресурс, що належить до екосистеми; Л', — біомаса і-го виду; т, — коефіцієнт природної смертності; А, — коефіцієнт засвоєння і-м видом біомаси (ї - 1)-го виду; ^і(^і) ~~ трофічна функція, що свідчить про інтенсив-
ність взаємозв'язків типу «хижак — жертва»; а, < 1 — частка відновленого деструкторами ресурсу, що містив- ся у відмерлій біомасі і-го виду (характеризує замкну- тість трофічного ланцюга).
У разі незамкнутого трофічного ланцюга останній член правої частини першого рівняння системи (3.6.1), який виражає масу біогенних елементів, що надходять унаслідок розкладання органічних речовин відмерлої біомаси, буде відсутнім (обведений пунктиром).
Математичні моделі спрощеного трофічного ланцюга водної екосистеми
Розглянувши випадок, коли зовнішнім ресурсом є маса біогенних елементів (азот, фосфор та ін.) з потоком <?«,■ Д — біомаса продуцентів, призначених для харчуван- ня організмів наступного трофічного рівня зі швидкістю Л7Х — трофічна функція, К0Л'1, У0— біомаса організмів другого трофічного рівня, наприклад тварин-фітофагів (рослиноїдних), з урахуванням третього трофічного рівня — хижаків з біомасою И2, одержимо систему трьох диференціальних рівнянь:
^г = Яі-У*Нх, (3-6.2) аі
^ = А^ЛГ, - т,*! - У^2, (3.6.3) аі
— = - ЩІЇ2 - У&. (3.6.4)
аі
Система рівнянь (3.6.2)—(3.6.4) є спрощеною мате- матичною моделлю, яка описує трофічний незамкнений ланцюг, що охоплює рослини, тварин-фітофагів і хижа- ків. Якщо хижаками вважати рибу, що систематично виловлюється, то в праву частину останнього рівняння системи (3.6.1) потрібно додати член (-У2Я), який характеризує швидкість (інтенсивність) вилову.
Використовуючи розв'язки системи (3.5.2), (3.5.3) та позначення
гі = *і^о ~ ті> г2 32 АгК, - т2, (3.6.5) NI = В, *2 = Р, Д(0) = і?0, В(0) - В0, Р(0) = Р0, (3.6.6)
запишемо розв'язок даної системи в такому вигляді:
г, г,2г2 г,г2г
---2-+--^- Є +
1 ТГЯ Г1Г2<Г2 - Гі) )
п _ШЩі + УоУ.ЬРо-УМ^ (3.6.7,
ГІГ2 , ГЛГ2-Гі) )
_ущ^Ш9* (3.6.8)
г2(г3 -Л)
Р(0 = М + (р0_М]е^ (3.6.9,
Одержані розв'язки (3.6.7,—(3.6.9, виражаються через показникові функції (експоненти,, які можуть мати додатні (рис. 3.24, і від'ємні (рис. 3.25, показники залежно від значень коефіцієнтів кх, т,, к2, т2. Для полегшення побудови графіків розв'язків системи рів- нянь (3.6.2,—(3.6.4, доцільно знайти стаціонарні розв'язки, тобто розв'язки при усталеному (стаціонар- ному, режимі описуваного моделлю процесу взаємодії фітопланктону, зоопланктону і риби. При стаціонарно- му режимі біомаси гідробіонтів не змінюються, тобто швидкості їх зміни дорівнюють нулю.
Отже, прирівнявши до нуля праві частини системи (3.6.2,—(3.6.4,, одержимо модель стаціонарного проце- су (якщо він існує,:
<?0 - У0В = 0,
гхВ-УхР = 0, (В = N^, Р = іУ2). (3.6.10,
[г2Р-У2Я = 0,
Розв'язавши систему лінійних алгебраїчних рів- нянь (3.6.10,, отримаємо
Р--^. ВОТ=Щ^. Д.-&. (3.6.11,
Рівність (3.6.11, може бути умовою стаціонарності лише у випадку, коли
Вя « В^, 4 = УЖ, Г[ = ^ - щ, г2=к2У1-т2. (3.6.12,
^0 Г1Г2
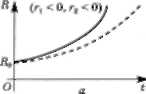
Стаціонарні розв'язки на рис. 3.24 і 3.25 зображено у вигляді горизонтальних пунктирних прямих, що є асимптотами нестаціонарних розв'язків. Перейдемо до короткого аналізу зображених на рис. 3.24 і 3.25 дея- ких кривих, які являють собою графіки нестаціонарних розв'язків (3.6.7)—(3.6.9). Форма і розташування пер- шої групи графіків, побудованих за формулами (3.6.5)—(3.6.9) за умови, що гх > г2 > 0 (рис. 3.24), пока- зують динаміку біомас (чисельності) фітопланктону, зоопланктону і риби у разі, коли народжуваність (швид- кість розмноження популяції) перевищує природну смертність. Однак і за таких ситуацій динаміка біомаси риб (рис. 3.24, в) залежить від співвідношення
_ '2*0
V**
(3.6.13)
що характеризує інтенсивність вилову риби.
V, < г„ гЛ < Уг9
Ч (г,<г8<0)
Вї
рк\ (г8>0)
(г. < 0)
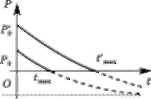
в в Рис. 3.24. Графіки при г, > 0, г, > 0 Рис. 3.25. Графіки при г, < 0. г, < 0
Графік показує, що при Ь < 1 (/"гР0 < У2Я) функція Р(() є монотонно спадною і в точці (= перетинає вісь Оі, тобто при такому вилові риби через гтвх років риба у водоймищі зникне. Якщо величину вилову У2Я зменши- ти, то рік г'т„, коли риба у водоймищі буде ПОВНІСТЮ виловлена, настане пізніше (на рис. 3.24, в точка пере- тину ( - ('„,„, пунктирної лінії з віссю 01).
За перевищення народжуваністю вилову (Ь > 1) іхтіомаса (кількість риби) з кожним роком збільшуєть- ся, відповідно до графіка, розташованого на рис. 3.24, в над асимптотою Р = Рсг
На рис. 3.24, а, б зображено графіки динаміки фіто- планктону та зоопланктону для випадків г, < Ух та г, > Ух. Рівняння (3.6.2)—(3.6.4) описують інші можли- ві випадки (сценарії) розвитку популяцій гідробіонтів. Зокрема, на рис. 3.25, а, б, в зображено графіки розв'яз- ків даної системи рівнянь за умови, що народжуваність (розмноження) менша за смертність гх < г2 < 0. Графік на рис. 3.25 свідчить, що біомаса (чисельність) зоо- планктону і риб, які ним живляться, швидко зменшу- ється, а біомаса фітопланктону — стрімко зростає. Динаміка біомас гідробіонтів В, В і Р залежить не тіль- ки від параметрів (?0, кх, тх, кг, т2, а й від початкових умов В0, В0 і Р0.