42.Бас параметрлердің сенімділік шектерін сипаттаңыз.

Әрьір тәжірбиенің түпкілікті мақсаты зерттелуші тәжірбие варианттарының арасында сенерліктей айырмашылықтардың бар немесе жоқ екендігін дәлелдеу болып табылады.Екіорта шама арасындағы айырымның сенімділігін сол айырымның өз қатесіне қатынасы арқылы анықтайды. md=

Қазіргі таңда айырымның сенімділігі стьюдент критериі Т-мен анықталады.

Сенімділіктің 3түрін өндірістік,биологиялық,экономикалық қолданамыз. Егер 0,95 ықтималдылығы тәжірбие мәліметтерінің 95%ы дәлелденген,ал 5%ы қате болуы мүмкін. Ал 0,99 ықтималдылықта 99%дәлелденген ,ал 1%ы әртүрлі қателіктер нәтижесінде болуы мүмкін .

43. Бас параметрлерді бағалау. Стьюдент шегінің стандартты кестесімен жұмыс жүргізіңіз. Әрбір тәжірибенің түпкілікті мақсаты зерттелуші тәжірибе варианттарының арасында сенерліктей айырмашылықтардың бар немесе жоқ екендігін дәлелдеу болып табылады. (Өндірісте егіліп жүрген сорттармен селекционердің жаңадан алған сорттарының өнімділіктері арасындағы айырмашылық, ерілген тыңайтқыштар әсерінен дақылдар өнімділігінің өзгеру айырмашылығы, өсімдіктер мен жануарлар түрлерінің арасындағы сандық көрсеткіштер, т.б)

Жоғырыдағы іріктеулер үшін табылған арифметикалық орта шамаларының өзгеріп отыратындығы соншалық, оның қанша мөлшерге өзгеретіндігін көрсету үшін, әрбір орта шамамен оның қатесін де көрсетіп жазу керек: Х±m=25,0±2,2

Орта шама 22,8-ден 27,2-ге дейін өзгеретіндігі көрінеді. Қате (m) квадраттық ауықтқудың негізінде есептелетін болғандықтан, орта шаманың мүмкін боларлықтай барлық мөлшері немесе дәліректеу шекарасында жатады, яғни вариациялық қатардың барлық варианттары х±3б немесе х±3,5б шекарасына сиятындықтары сияқты. Осыдан 3m немесе 3,5m мағыналары арифметикалық орта шаманың шегіне жеткен қатесі деп аталады.

Екі орта шама арасындағы айырманың сенімділігін сол айрманың өз қатесін қатынасы арқылы анықтайды. Айырманың қатесі қателіктер квадраттарының қосындысынан табылатын квадраттық түбірге тең:md=√m²+m²

Мысалы, ылғалдың жетіспеушілігі жағдайларында жаздық бидай өнімділігіне фосфор тыңайтқыштарының әсерін зерттеу тәжірибесінен мынадай мәліметтер алынды (тәжірибе 4 рет қайталанумен жүргізілді):

Бақылау (тыңайтқышсыз) –11,5±0,2 ц/га

Суперфосфатпен өңдегенде-13,1±0,3 ц/га

Алынған артық өнім серліктей ме? Орта шамалар арасындғы айырма:13,1-11,5=1,6ц/га.

Айырманың қатесі: md=√0,2²+0,3²=√0,13=0,36

Биометрия бойынаша ескі оқу құралдарында, егер бұл қатынас 3-ке немесе одан де көбірекке тең болса, айырма сенімді деп көрсетіледі. Ал қазір одан да дәлірек, айырманың сенімділігі стьюдент критериі-t-мен анықталады; t айырманың өз қатесі қатынасына тең.

Қарастырылған тәжірибеде қайталанулар саны төрттен. Демек, ерікті дәрежелер саны 4+4-2=6. Ерікті дәрежелер 6 санына 0,95 ықтималдылықта (5% деңгейде) t-ның сенімділігі 2,45 болса, ал 0,99 ықтималдылықта (1% деңгейде) t-ның сенімділігі 3,71-ге тең. Демек, бақылау және тәжірибе варианттары өнімдері арасындағы айырма 0,99 ықтималдықтан да жоғары деңгейде сенімді.

44.Жеке жиынтық бойынша жалпы көрсеткішті бағалауды және тәжірибенің дәлдігін есептеңіз. Тәжірибенің дәлдігі. Белгілер әртүрлілігінің көрсеткіштері қызметін лимиттер өзгергіштіктің шайқалу шегі,орташа квадраттық ауытқу б –сигма варианса б² және варияция коэффициенті С.v атқарады. Америка генетигі Дж. Л. Брюйбекер өзінің «Ауылшаруашылығы генетикасы» деген кітабында мысал ретінде екі баскетбол командасы ойыншыларының футпен және дюймамен келтірілген бойларының биіктігін келтіреді ( фут = 0,3м дюйм = 2,54см)Өгіздердің тірі салмағы екі совхозда да орта есеппен бірдей – 650 кг-нан; бірақ өгіздердің салмақтарының әртүрлілігі екінші совхозда бірінші совхозға қарағанда 5 есе көп. Осы әртүрлілік лимиттер мен өзгергіштіктің шайқалу шегі арқылы көрсету қолайлы болып шығады. Lim1 = 640 – 660 кг (20кг)Lim2 = 600 – 700 кг (100 кг) Бірталай жағдайларда топтардың әртүрлілігін лимиттер мен өзгергіштіктің шайқалу шегі арқылы көрсетудің үлкен өндірістік маңызы бар, олар белгілі бір продукцияға ақша төлеу үшін негіз етіп алынады. Вариация коэффициенті С.v. атқарады. Әртүрлілік көрсеткіштерінің бәріне тән жалпы қасиет олар осы саналуан әртүрлілік ерекшеліктерінің қандай дәрежесі болса да нақты белгілей алады. Әртүрлі белгілер бойынша өзгергіштік дәрежесін, сол сияқты жекелеген обьектілердің өзгергіштік дәрежесін салыстыру үшін өзгергіштік коэффициенті қолданылады. Өзгергіштік коэффициенті орта шамадан проценттер мен көрсетілген квадраттық ауытқу болып табылады, өзгергіштік коэффициенті C*v – мен белгіленеді және төмендегі формула бойынша табылады:

cv= ;Өзгергіштік коэффициенті әр уақытта процентпен көрсетіледі. Оның көмегімен өзгергіштігі сан алуан обьектілерді олардың әртүрлі көрсеткіштері бойынша бір бірімен салыстыруға болады. Көптеген биологиялық зерттеулер арқылы өзгергіштік коэффициенттерін табудың үлкен маңызы бар. Мысалы, өсімдіктің жаңа сортын шығаруды өз алдына мақсат етіп қойған селекционер ең алдымен бастапқы материалдағы әртүрлі белгілердің өзгергіштік коэффициентін зерттейді. Себебі, сұрыптау үлкен өзгергіштіктері бар белгілер бойынша жүргізілсе ғана жақсы нәтиже бере алады. Өндіріске беруге дайын сортта үлкен өзгергіштік коэффициенті болуы мүмкін емес – өйткені басты белгілермен көрсеткіштерінен сорт тұрақты болуы керек. Өзгергіштік коэффициентін зерттеуге әсіресе жануарлар мен өсімдіктердің морфологиясын, систематикасын немесе оларды аклиматизациялау жұмыстарымен шұғылданып жүрген адамдар үлкен маңыз береді.Белгілі математик Гаусс әртүрлілік дәрежесінің көрсеткіші ретінде негізгі ауытқуды пайдалану керектігін ұсынды. Ол орта шамадан ауытқулар квадраттарымен жиіліктердің көбейтінділерінің қосындысын бақылаулар санына бөліп квадрат түбірін тапқанда шыңатын санға тең. . Өзгергіштіктің шайқалу шегі неғұрлым аз болса, сигманың мәні де соғұрлым аз болады. Егер өзгергіштік жоқ болса сигма=0.Зерттеу үшін алынған әрбір жеке жиынтықтардың жекелеген даналары орта мөлшерден әр дәрежеде ауытқиды, сондықтан зерттеулерге тиісті іріктеуді сипаттау үшін тек арифметикалық орта шаманы табу жеткіліксіз. Мұндайда осы әртүрлілік дәрежесін сипаттай алатындай көрсеткіштер келтіру керек.

Тәжірибенің дәлдігін анықтаудың үлкен маңызы бар. Өйткені тәжірибе арқылы алынған мәліметтердің сенімділік дәрежесі анықталады.Тәжірибенің дәлдігі Р арқылы белгіленеді және мына формуламен анықталады: Р= m x 100/X, яғни, қатенің арифметикалық орта шамаға пайыздан алған қатынасын есептеу арқылы табылады.Егер Р-нің мәні 3 % - тен кем болса, тәжірибе жеткілікті мөлшерде дәл есептелін

еді,егер Р-нің мәне 5 % болса – қанағаттанарлық деп есептелінеді, Егер Р-нің мәні 6-7%-ға тең немесе одан артық болса, алынған қорытындыларға сақтықпен қарауға тура келеді. Тәжірибені методиканың барлық шарттарын сақтай отырып, қайталау керек.

45. Орта арифметикалық шаманың қатесін аз мөлшердегі іріктемелерде есептеу және тәжірибенің дәлдігін табыңыз.

Варианттары көп, ал қайталанылу саны азырақтау  тәжірибе 

мәліметтерін өңдеген кезде арифметикалық орта шаманың  қатесін 

жеңілдеу жолмен де есептеп шығаруға болады. Ол үшін Молденгауэр

 факторын (констант К) пайдалана отырып мына формула бойынша 

есептейді: m =  ║ a║ * K. Мұнда ║ a║   таңбадан тәуелсіз ауытқулардың

 қосындысы, ал К-мына 

формула:                                                        К = 1/ 0.79788*√n–1 бойынша есептеп 

шығарылған, қайталанулардың санына қарай өзгеріп отыратын 

константа. П.Н. Константиновтың ‘‘Дала тәжірибелер методикасы’’  

кітабында орта шамалардың қателер үшін  К-константалары кестесі 

келтірілген. 

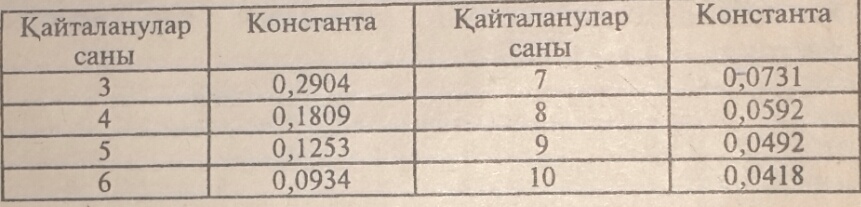
Қайталанулар саны көп болған жағдайда қателіктерді жеңілдеу жолмен 

есептеу көп уақыт үнемдеуге көмектеспейді. Мысалы әртүрлі микроэлементтердің әртүрлі дозасының бидай өнімділігіне тигізетін әсерін зерттедік дейік. Бізде тәжірибенің 40 варианты болды. Әр варианта 4 рет қайталану арқылы сыналды. Тәжірибенің бірінші  вариантының мынадай өнім алынды. 

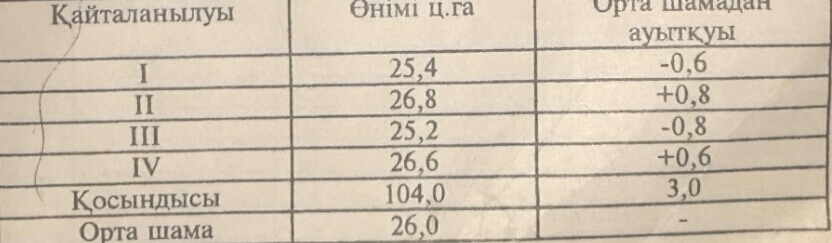Орта шаманың және ауытқулардың дұрыс есептелгендігін тексеру үшін 

біз алдымен оң және теріс ауытқулардың қосындысын табамыз: -0,6 + (-

0,8)=-1,4     +0,8+0,6=+1,4. Бұл есептеулер тек тексеру үшін ғана керек 

және келешектегі есептеулерге ешқанда қатыспайды. Оң және теріс 

ауытқулардың қосындысы бір-біріне тең, демек есептеулер дұрыс 

жасалған. Ауытқулардың таңбасына қарамай қосындысын табамыз, 

сосын 4 қайталану үшін берілген 0,1809 тең константаға көбейтеміз. 3,0 

* 0,1809 = 0,5427 Орта шама  26±0,54 ц. Тәжірибенің дәлдігі.Тәжірибенің дәлдігін анықтаудың үлкен маңызы бар. Өйткені тәжірибе арқылы алынған мәліметтердің сенімділік дәрежесі анықталады.Тәжірибенің дәлдігі Р арқылы белгіленеді және мына формуламен анықталады: Р= m x 100/X, яғни, қатенің арифметикалық орта шамаға пайыздан алған қатынасын есептеу арқылы табылады.Егер Р-нің мәні 3 % - тен кем болса, тәжірибе жеткілікті мөлшерде дәл есептелін

еді,егер Р-нің мәне 5 % болса – қанағаттанарлық деп есептелінеді, Егер Р-нің мәні 6-7%-ға тең немесе одан артық болса, алынған қорытындыларға сақтықпен қарауға тура келеді. Тәжірибені методиканың барлық шарттарын сақтай отырып, қайталау керек.

46. Негізгі статистикалық көрсеткіштерді «Момент тәсілі» арқылы есептеуді көрсетіңіз.

Варианттарының саны көп күрделі вариациялық қатарларды өңдеген кезде арифметикалық орта шаманы есептеу үшін «моменттер әдісі» қолданылады.Жай вариациялық қатарды мысал етіп алып, осы әдіс бойынша қалай есептеу керектігін қарастырайық.

Варианттар х	Кез келген орта шамадан ауытқулар х-х0
10 11 12	-3 -2 -1
13	-6
14 15 16 17	1 2 3 4 10

Алынған кездейсоқ орта шамадан ауытқулар а немесе х арқылы белгіленеді. Кездейсоқ алынған орта шама ретінде вариациялық қатардың дәл ортасында немесе ортасына жақын жатқан , кез келген вариантаны аламыз және оны қос түзу сызықпен белгілеп шектейміз.Келтірілген мысалда, кездейсоқ орта шама ретінде 13 вариантын алдық. Әрбір варианттың кездейсоқ, шартты орта шамадан жоғары жатқан варианттар (-) белгісімен, төмен жатқан варианттар (+) белгісімен белгіленеді. Осы ауытқулардың алгебралық қосындысы: -6+10=+4 санға тең болады. Әдетте, орта шамадан оң және теріс ауытқулардың қосындысы нөлге тең болады. Сондықтан, варианттардың орта шамадан ауытқу (х-х0) мәнін бақылаулар санына (8-ге бөліп,в әрпімен белгіленген түзетпені табады: в=4/8=0,5. Түзетудің формуласы: ; ал нақты орта шама кездейсоқ шартты орта шамамен (М0) түзетпенің (в) қосындысына тең, яғни M=M₀±(-b).Тапқан (в) алгебралық қосынды екенін және ол түзету оң (+) немесе (-) таңбалы болуы мүмкін екенін әрине естен шығармау керек.Егер теріс таңбалы түзету алынса, онда M=M₀+(-b), ал оң таңбалы түзету алсақ ,M=M₀+b.Біздің мысалымызда түзетпе мәні (в) оң таңбалы сан болғандықтан ,М=13+0.5=13.5.Есебімізді тексеріп көрейік: n=8, яғни кездейсоқ шартты орта шамамен есептеп шығарғандағыдай нәтиже алынды.Арифметикалық орта шаманы варианттары бірнешеу болып келетін күрделі вариациялық қатардан тапқан кезде де, осы сияқты ортада жатқан бір вариантты кездейсоқ шартты орта шама ретінде алады да ауытқуларын есептейді.Онан соң ауытқуларды өзінің тиісті жиіліктеріне көбейту арқылы оң және теріс ауытқулардың алгебралық қосындысын табады да, оны бақылау санына бөледі.Осылайша табылған түзетуді өзінің таңбасына қарай кездейсоқ шартты орта шамаға қосады немесе одан алып тастайды.