17 Өзгергіштік көрсеткіштері және оларды статистикада қолдану жолдарын көрсетіңіз:
Белгілер әртүрлілігінің көрсеткіштері қызметін лимиттер өзгергіштіктің шайқалу шегі,орташа квадраттық ауытқу б –сигма варианса б2 және варияция коэффициенті С.v атқарады. Америка генетигі Дж. Л. Брюйбекер өзінің «Ауылшаруашылығы генетикасы» деген кітабында мысал ретінде екі баскетбол командасы ойыншыларының футпен және дюймамен келтірілген бойларының биіктігін келтіреді ( фут = 0,3м дюйм = 2,54см)Өгіздердің тірі салмағы екі совхозда да орта есеппен бірдей – 650 кг-нан; бірақ өгіздердің салмақтарының әртүрлілігі екінші совхозда бірінші совхозға қарағанда 5 есе көп. Осы әртүрлілік лимиттер мен өзгергіштіктің шайқалу шегі арқылы көрсету қолайлы болып шығады. Lim1 = 640 – 660 кг (20кг)Lim2 = 600 – 700 кг (100 кг) Бірталай жағдайларда топтардың әртүрлілігін лимиттер мен өзгергіштіктің шайқалу шегі арқылы көрсетудің үлкен өндірістік маңызы бар, олар белгілі бір продукцияға ақша төлеу үшін негіз етіп алынады. Мысалы, қақталып тұздалған тұтас еттің бір партиясының М1 = 90 кг, lim1 = 88-92 (4кг), ал екіншісінің М2 = 90 кг, lim2 = 80-100 (20) кг болсын делік. Әрине, бірінші партияның еттері екіншісіне қарағанда стандарт ретінде жоғары бағаланады.Орташа квадраттық ауытқу.Белгілі математик Гаусс әртүрлілік дәрежесінің көрсеткіші ретінде негізгі ауытқуды пайдалану керектігін ұсынды. Ол орта шамадан ауытқулар квадраттарымен жиіліктердің көбейтінділерінің қосындысын бақылаулар санына бөліп квадрат түбірін тапқанда шыңатын санға тең,σ – орташа квадраттық ауытқу; Өзгергіштік коэффициенті әр уақытта процентпен көрсетіледі. Оның көмегімен біз өзгергіштігі сан алуан объектілерді олардың әртүрлі көрсеткіштері бойынша бір-бірімен салыстыра аламыз. Өзгергіштік коэффициенттерін табудың үлкен маңызы бар. Сұрыптау үлкен өзгергіштіктері бар белгілер бойынша жүргізілсе ғана жақсы нәтиже бере алады.Әртүрлі белгілер бойынша өзгергіштік дәрежесін, сол сияқты жекелеген объектілердің өзгергіштік дәрежесін салыстыру үшін өзгергіштік коэффициенті қолданылады. Өзгергіштік коэффициенті орта шамадан проценттермен көрсетілген квадраттық ауытқу болып табылады, өзгергіштік коэффициенті C●v –мен белгіленеді және төмендегі формула бойынша табылады:C●v=(𝑏●100)/𝑥%;b– орташа квадраттық ауытқу;M – арифметикалық орта шама;
18 Варияциялық қатардың анықтамасы, оны құрудың тәсілдерін және график арқылы өрнектеуді көрсетіңіз Варианттардың төменнен жоғарыға,жоғарыдан төменге кеміп орналасу тәртібі варияциялық қатарды құрайды.Варияциялық қатар құру ∑максимал және минимал варианттар табылады да, олар белгіленеді.Варияциялық қатар құру үшін варианттарды өсу тәртібімен орналастырамыз.Онан соң варианттарды тарата отырып алынған іріктеуде әрбәр варианта қанша рет кездесетіндігін анықтаймыз.Белгілі бір іріктеуде әрбір варианттың неше рет кездесетіндігін көрсететін сан жиілік деп аталады және оны f әрпімен белгілейміз
х |
F |
12 |
2 |
13 |
6 |
14 |
8 |
15 |
13 |
16 |
8 |
17 |
7 |
18 |
3 |
19 |
2 |
20 |
1 |
∑f=50 Мысалы:Біздің мысалымызда минимал варианта мен максимал вариантаның арасындағы айырма өзгерудің тербелу өрісі немесе өзгергіштіктің шайқалу шегі деп аталады. Жиілікті анықтау үшін варианттарға тарату жүргізіледі.1 кестеде масақшалар санын көрсететін бірінші цифр 18-ді сызып тастаймыз да варияциялық қатардағы 18-ші вариантаның қасына нүкте қоямыз.Варианттарды осылайша таратып біткен соң нүктелер мен сызықтарды цифрлармен ауыстырамыз да f әрпімен белгіленген жиілікті табамыз.Біздің мысалымызда жиіліктердің қосындысы 2+6+8+12+8,,,+=50 ге тің, демек тарату дұрыс жүргізілген.Таратудың дұрыс жүргізілгенін міндетті түрде тексеру керек,әйтпесе тарату кезінде жіберілген және байқалмаған қате одан әрі жасалатын жұмыстың бәрін қате етеді.Варияциялық статистикада қосынды грек алфавитінің бас әрпі сигма -∑ мен белгіленеді.Зерттелген обьектілердің саны латын n-мен белгіленеді.Сонымен бірінші формула былай жазылады:∑f=n Өзіміз жасаған варияциялық қатарды енді график арқылы бейнелейік горизанталь оське варианттарды, вертикаль оске жиіліктерді саламыз. Варияциялық қатарды графика арқылы бейнелеу варияциялық қисық деп аталады.Варияциялық қатарда ең көп кездесетін вариантаны мода деп атайды.Варияциялық қатардың қақ ортасында орналасқан варианта медиана деп аталады.Мода Мо ал медиана Ме белгілерімен белгіленеді.Cандық сапалықӨзгергіштік деп –туыстас бір топқа жататын особьтардың арасындағы айырмашылықты айтады.Өзгергіштік барлық тірі организмдерге тән қасиет.Табиғатта сандық және сапалық өзгергіштіктер байқалады.Сандық өзгергіштікке:масақтағы дәндердің әртүрлі саны,өсімдіктердегі жемістің саны, тауық жұмыртқаларының саны мысал бола алады.Сапалық өзгергіштіктерге:өсімдік гүлдерінің сан алуан түстері,формалары,жемістердің дәмі,өсімдік жапырақтарының түсі жатады.Сандық өзгергіштік санаулармен,өлшеулермен немесе химиялық талдаумен зерттеледі.Өзгергіштікті үзілісті немесе үзіліссіз деп бөледі.Үзілісті өзгергіштіктер санау жолымен зерттеледі және осылайша аталу себебі зерттелетін особьтардың арасындағы айырмашылық әр уақытта 1 ден кем болмайтын бүтінсандар арқылы белгіленеді.Мысалы: Бидайдың масағында 10, 15 ,20 ,25 т.б дәндер болуы ммкін бірақ 10,5 дән болуы мүмкін емес.Үзілісті өзгергіштіктер: өлшеулер,химиялық талдаулар жасау жолымен анықталады.Мұндай жағдайда зерттелетін сандық белгілер бүтін сандар арқылы да және бөлшек сандар арқылы да беріле алады.
19) Сандық және сапалық, үзілісті және үзіліссіз өзгергіштіктерге сипаттама? Өзгергіштік деп-туыстас бір топқа жататын особьтардың арасындағы айырмашылықты айтады. Өзгергіштік барлық тірі организмдерге тән қасиет. Ол сыртқы орта жағдайларның әсерінен (модификациялық өзгергіштік) н/е организмнің тұқым қуалаушылық қасиеттерінің өзгеруі әсерінің (мутациялық ж/е комбинативтік өзгергіштіктер) пайда болады. Табиғаттан сандық және сапалық өзгергіштіктер байқалады. Сандық өзгергіштіктерге: масақтағы дәндердің әртүрлі саны, өсімдіктегі жемістердің саны, тауықтың жұмыртқаларының саны, сиырдың сүттілігі саны, тұқымдағы белоктар мен майлардың әртүрлі мөлшері т.б. мысал бола алады. Сапалық өзгергіштіктерге: өсімдік гүлдерінің сан алуан түстері, формалары, жемістердің дәмі, өсімдік жапырақтарының н/е жануарлар терілерінің сан алуан түстері т.б. мысал бола алды. Көпшілік жағдайда сапалық өзгергіштікті сандық өзгергіштіктерге айналдыруға болады, мысалы, гүлдердің түсі ондағы белгілі пигменттің мөлшеріне ж/е клетка шырынының қышқылдық дәрежесіне тәуелді, ал жемістердің дәмі олардағы қанттардың, қышқылдардың ж/е пектин заттарының мөлшеріне байланысты т.б. Сандық өзгергіштік санауларымен, өлшеулермен н/е химиялық талдаумен зерттелінеді. Өзгергіштіктерді үзілісті ж/е үзіліссіз деп ажыратады. Үзілісті өзгергіштіктер санау жолымен зерттеледі ж/е осылайша аталу себебі зерттелетін особьтардың арасындағы айырмашылық әр уақытта 1-ден кем болмайтын бүтін сандар арқылы белгіленеді. Мыс: бидайдың масағында 10, 15, 46 ж/е т.б. дәндер болуы мүмкін, бірақ 10,5 дән болуы мүмкін емес. Үзіліссіз өзгергіштіктер өлшеулер, химиялық талдаулар жасау жолымен анықталады. Мұндай жағдайдарда зерттелінетін сандық белгілер бүтін сандар арқылы да ж/е бөлшек сандар арқылыда беріле алады. Өлшеу неғұрлым дәліректеу болса, зерттелген обьектілердің арасындағы айырмашылық та соғұрлым аз болады. Мыс: екі нүктенің арасындағы қашықтықты біз километрмен, метрмен, сантиметрмен, милиметрмен өлшей аламыз ж/е өлшеуіміз неғұрлым дәлірек болса екі көрші өлшемдердің арасындағы айырмашылық соғұрлым аз болды.
20) Іріктеме алу тәсілдерін сипаттап, механикалық сұрыптау жолын сипаттаңыз? Механикалық іріктеу – жиынтық бірліктері белгілі бір тәртіппен орналасып, іріктемелі пайызға керісінше топтарға интевалдармен бөлінетін іріктеу тәсілі. Біркелкі шамалардың біраз саны статистикалық жиынтық деп аталады. Статистикалық жиынтық жалпы және жекелеген жиынтықтар болуы мүмкін. Егін даласында бірдей жағдайда өсірілген бір сорттың өсімдіктері жалпы статистикалық жиынтық болып табылады. Біз қанша талпынсақ та, осы сортқа жататын барлық өсімдіктертің биіктігін өлшеп шығуға, олардың масағындағы дәндерінің санын н/е басқа көрсеткіштерін тегіс есептеп шығуға шамамыз келмейді. Сондықтан бұларды зерттеу үшін жеке жиынтықты н/е іріктеуді, яғни егін даласының бөліктерінен алынған өсімдіктердің белгілі санын пайдаланамыз. Дұрыс алынған іріктеу жалры статистикалық жиынтықтың қасиеттері жөнінде пікір айтуға мүмкіндік береді. Іріктеуді қалайша жүргізгенде дұрыс нәтиже беретіндігіне мысал келтірейік. Ротамштет тәжірибе станциясында мынандй тәжірибе жасалды. Сол станцияның егін даласында кездесетін тастардың орташа мөлщерін анықтау керек болды. Бір топ қызметкерлер көз мөлшерімен ірілі-ұсақ тастардың орташа мөлшерін анықтады ж/е толық зерттеу үшін тек осы орташа тастарды ғана алады. Екінші топтың қызметкерлері зерттеу үшін егін даласының диагоналы бойымен жүре отырып, әрбір белгілі қашықтықта кездескен ірілі-ұсақ тастарды таңдамай ала берді. Математикалық өңдеу мынаны көрсетті. Бірінші топтың қызметкерлері тапқан тастардың орташа мөлшері әрбір қызметкерлердің жеке ерекшеліктеріне қарай әртүрлі болып шықты. Екінші топ қызметкерлері есептеп шығарған тастардың орташа мөлшері бәрінде бірдей болып шықты. Әдейі емес, іріктеулерді кездейсоқ сұрыптау рендомиздік сұрыптау деп аталады. Іріктеулерді сұрыптаудың бұл категориясына талдау жүргізу үшін заттың әрбір 10-шы, 20-шы, 30-шы т.б. даналарын алу жатады, мысалы, балықтардың өзгергіштігін зерттегенде н/е жүгерінің собықтарына талдау жасағанда ж/е басқа да көптеген жағдайларда.
21) Жеке жиынтық (іріктеме) оның қасиеттері, алу тәсілдерімен таныстыру? Біркелкі шамалардың біраз саны статистикалық жиынтық деп аталады. Статистикалық жиынтық жалпы және жекелеген жиынтықтар болуы мүмкін. Егін даласында бірдей жағдайда өсірілген бір сорттың өсімдіктері жалпы статистикалық жиынтық болып табылады. Біз қанша талпынсақ та, осы сортқа жататын барлық өсімдіктертің биіктігін өлшеп шығуға, олардың масағындағы дәндерінің санын н/е басқа көрсеткіштерін тегіс есептеп шығуға шамамыз келмейді. Сондықтан бұларды зерттеу үшін жеке жиынтықты н/е іріктеуді, яғни егін даласының бөліктерінен алынған өсімдіктердің белгілі санын пайдаланамыз. Дұрыс алынған іріктеу жалры статистикалық жиынтықтың қасиеттері жөнінде пікір айтуға мүмкіндік береді. Іріктеуді қалайша жүргізгенде дұрыс нәтиже беретіндігіне мысал келтірейік. Ротамштет тәжірибе станциясында мынандй тәжірибе жасалды. Сол станцияның егін даласында кездесетін тастардың орташа мөлщерін анықтау керек болды. Бір топ қызметкерлер көз мөлшерімен ірілі-ұсақ тастардың орташа мөлшерін анықтады ж/е толық зерттеу үшін тек осы орташа тастарды ғана алады. Екінші топтың қызметкерлері зерттеу үшін егін даласының диагоналы бойымен жүре отырып, әрбір белгілі қашықтықта кездескен ірілі-ұсақ тастарды таңдамай ала берді. Математикалық өңдеу мынаны көрсетті. Бірінші топтың қызметкерлері тапқан тастардың орташа мөлшері әрбір қызметкерлердің жеке ерекшеліктеріне қарай әртүрлі болып шықты. Екінші топ қызметкерлері есептеп шығарған тастардың орташа мөлшері бәрінде бірдей болып шықты. Әдейі емес, іріктеулерді кездейсоқ сұрыптау рендомиздік сұрыптау деп аталады. Іріктеулерді сұрыптаудың бұл категориясына талдау жүргізу үшін заттың әрбір 10-шы, 20-шы, 30-шы т.б. даналарын алу жатады, мысалы, балықтардың өзгергіштігін зерттегенде н/е жүгерінің собықтарына талдау жасағанда ж/е басқа да көптеген жағдайларда.
22) Таралу полигоның сызыңыз. Вариациялық қатардан гистограмма сызу жолын көрсетіңіз? Кластарға жіктелген вариациялық қатарды график арқылы бейнелеу гистограмма деп атайды. Гистограмма жасаған кезде горизонталь осьтің бойына кластардың мөлшерін, ал вертикаль осьтің бойына жиіліктерді орналастырады. Гистограмманы вариациялық қисыққа айналдыруға болады. Ол үшін кластардың ортасын түзу сызықтармен қосу керек. Жүгері өсімдігінің биіктігі бойынша алынған өзіміздің мәліметтерімізді гистограммамен бейнелейік.
Талдау кезінде әдетте зерттеуші көп санды мәліметтер алады. Гистограммалар мен вариациялық қисықтар құру сол алынған көп санды мәліметтердің мәнін түсінуге ж\е олардан қандай да болмасын белгілі заңдылық табуға көмектеседі. Графиктер көбінесе баспа жұмыстарында ж/е ғылыми зерттеу жұмыстары бойынша жазылатын отчеттарда жиі орын алады. Салыстыруға ыңғайлы болу үшін бір чертежде кейде бірнеше қисықтар беріледі. Жұмыс чертеждарында бұл қисықтарды әртүсті туштармен н/е қарындаштармен сызған ыңғайлы. Баспаға беру үшін дайындалған қисықтарды әдетте қара тушьпен, бірақ әртүрлі шрифтармен сызады. Әрбір чертежде тәжірибенің варианттары қалай бейнеленгенін көрсететін экспликация болуы қажет. Бір чертежда тәжірибенің 5-6 вариантынан артық орналастыру ыңғайсыз болады. Сондықтан, егер тәжірибенің салыстырылатын варианттары көп болса бірнеше графиктер сызу керек, ж/е әрбір чертежде контроль қызметін атқаратын варианта орналастырылады. Бір чертежге кейде бірнеше қисықтар сыйғызу керек болады. Ол үшін варианттарды кластарға жіктеу кезінде кластардың шекараларын әр тәжірибенің варианты бойынша емес, барлық варианттар үшін жалпы бірдей боларлықтай кластар шекарасын алу керек. Мысалы егер өсімдіктің минимал биіктігі тәжірибенің бір вариантында 98см, екіншісі 100, үшіншісі 113см болып, алкластың мөлшері =10см деп алсақ, онда кластардың шекаралары мынадай болуы қажет: 90-99, 100-119, 110-119 т.б. Бірінші кластың мүлде болмауы ешқандай роль атқармайды. Көптеген ауылшаруашылық ж/е биологиялық обьектілердің белгілері үшін ол белгілердің қалыпты таралуы тән, яғни белгілердің жекелеген варианттары мөлшері неғұрлым орта шамадан алшақтаған сайын, ол вариант соғұрлым сирек кездесетін болады. Мысалы көпшілік адамдар орта бойлы. Алып адамдар (биіктігі 200 см-ден артық болатын) ж/е өте аласа адамдар (биіктігі 100 см-ден кем) өте сирек кездеседі.
23) Басты ж/е жеке жиынтық (іріктеме) олардың қасиеттерін сипаттаңыз? Біркелкі шамалардың біраз саны статистикалық жиынтық деп аталады. Статистикалық жиынтық жалпы және жекелеген жиынтықтар болуы мүмкін. Егін даласында бірдей жағдайда өсірілген бір сорттың өсімдіктері жалпы статистикалық жиынтық болып табылады. Біз қанша талпынсақ та, осы сортқа жататын барлық өсімдіктертің биіктігін өлшеп шығуға, олардың масағындағы дәндерінің санын н/е басқа көрсеткіштерін тегіс есептеп шығуға шамамыз келмейді. Сондықтан бұларды зерттеу үшін жеке жиынтықты н/е іріктеуді, яғни егін даласының бөліктерінен алынған өсімдіктердің белгілі санын пайдаланамыз. Дұрыс алынған іріктеу жалры статистикалық жиынтықтың қасиеттері жөнінде пікір айтуға мүмкіндік береді. Іріктеуді қалайша жүргізгенде дұрыс нәтиже беретіндігіне мысал келтірейік. Ротамштет тәжірибе станциясында мынандй тәжірибе жасалды. Сол станцияның егін даласында кездесетін тастардың орташа мөлщерін анықтау керек болды. Бір топ қызметкерлер көз мөлшерімен ірілі-ұсақ тастардың орташа мөлшерін анықтады ж/е толық зерттеу үшін тек осы орташа тастарды ғана алады. Екінші топтың қызметкерлері зерттеу үшін егін даласының диагоналы бойымен жүре отырып, әрбір белгілі қашықтықта кездескен ірілі-ұсақ тастарды таңдамай ала берді. Математикалық өңдеу мынаны көрсетті. Бірінші топтың қызметкерлері тапқан тастардың орташа мөлшері әрбір қызметкерлердің жеке ерекшеліктеріне қарай әртүрлі болып шықты. Екінші топ қызметкерлері есептеп шығарған тастардың орташа мөлшері бәрінде бірдей болып шықты. Әдейі емес, іріктеулерді кездейсоқ сұрыптау рендомиздік сұрыптау деп аталады. Іріктеулерді сұрыптаудың бұл категориясына талдау жүргізу үшін заттың әрбір 10-шы, 20-шы, 30-шы т.б. даналарын алу жатады, мысалы, балықтардың өзгергіштігін зерттегенде н/е жүгерінің собықтарына талдау жасағанда ж/е басқа да көптеген жағдайларда.
24) Вариациялық қатар құрудың тәсілдерін сипаттаңыз. Вариациялық қатарды график арқылы өрнектеу тәсілін сипаттаңыз? Белгінің сандық көрсеткіші варианта немесе дата деп аталады ж/е v н/е x-пен белгіленеді. Варианттардың төменнен жоғарыға өсіп немесе жоғарыдан төменге кеміп орналасу тәртібі вариациялық қатар құрайды. Вариациялық қатар құру үшін максимал ж/е минимал варианттар табылады да, олар белгіленеді. Біздің мысалымызда минимал варианта 12, максимал вариант 20. Минимал варианта мен максимал вариантаның арасындағы айырма өзгерудің тербелу өрісі н/е өзгергіштіктің шайқалу шегі деп аталады. Вариациялық қатар құру үшін варианттарды өсу тәртібімен орналастырамыз. Онан соң варианттарды тарата отырып алынған іріктеуде әрбір варианта қанша рет кездесетіндігін анықтаймыз. Белгілі бір іріктеуде әрбір вариантаның неше рет кездесетіндігін сан жиілік деп аталады ж/е f әрпімен белгіленеді.
X |
Г |
12: |
2 |
13 |
6 |
14 |
8 |
15 |
13 |
16 |
8 |
17 |
7 |
18 |
3 |
19: |
2 |
20. |
1 |
Жиілікті анықтау үшін вапианттарға тарату жүргізіледі: масақшалар санын көрсететін бірінші цифр 18ді сызып тастаймыз да вариациялық қатардағы 18ші вариантаның қарсысына нүкте қоямыз.Онан соң екінші цифр 13ті сызып тастаймыз да 13ші вариантаның қарсысына нүкте қоямыз,үшінші цифрды сызамыз және 20шы вариантаның қарсысына нүкте қоямыз т.б 1,2,3,4 сандары тиісті нүктелер арқылы 5 ЖӘНЕ 6сандары диагоналдармен (х) 7,8,9,10 сандары квадраттың қабырғалары мен (х) белгіленеді.Варианттарды осылайша таратып біткен соң нүктелермен сызықтарды цифрлармен ауыстырамыз да f әрпімен белгіленген жиілікті табамыз.Жиіліктердің қосындысы зерттеу үшін алынған объектілердің санына тең болады.Біздің мысалымызда жиіліктердің қосындысы 2+6+8+12+8....+1=50ге тең,демек тарату дұрыс жүргізілген.Таратудың дұрыс жүргізілгендігін міндетті түрде тексеру керек,әйтпесе тарату кезінде жіберілген және байқалмаған қате одан әрі жасалатын жұмыстың бәрін қате етеді.Вариациялық статистикада қосынды грек алфавитінің бас әрпі сигма ∑-мен белгіленеді. Зерттелген объектілердің саны латын әрпі n-мен белгіленеді. Сонымен бірінші формула былай жазылады: ∑ḟ=n. Өзіміз жасаған вариациялық қатарды енді график арқылы бейнелейік горизонталь оське варианттарды, вертикаль оське жиіліктерді саламыз.
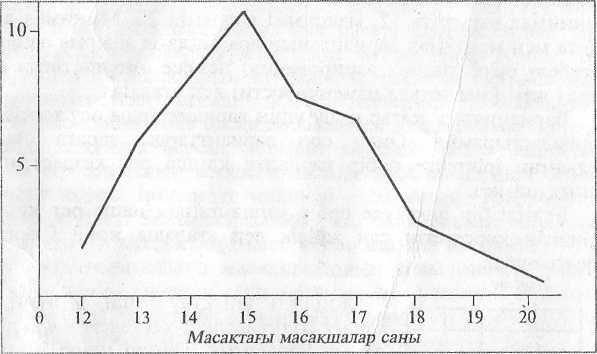
Жұмыс
графиктерін клеткалық н/е миллиметрлік
қағазда жасаған ыңғайлы. Вариациялық
қатарды график арқылы бейнелеу вариациялық
қисық деп аталады. Вариациялық қатардағы
ең көп кездесетін варианттаны мода деп
атайды. Біздің мысалымызда мода -15-ке
тең. Вариациялық қатардың ортасында
орналасқан варианта медиана деп аталады.
Мода Мо, ао медиана Ме белгілерімен
белгіленеді. Биологиялық зерттеулерде
моданың үлкен маңызы бар. Мысалы,
жоңышқалардың арасында көп рет шабылатын
және бір рет шабылатын формалары бар.
Олар бір-бірінен буын аралықтарының
саны арқылтарының саны арқылы ажыратылады.
Жоңышқаға апробция жүргізген кезде
бізге оның буынаралықтарының орташа
саны тұрақты болып келетін өсімдіктердің
саны керек, яғни көп шабылатын н/е бір
рет шабылатын формаларға жататын
өсімдіктер керек. Мода бізге қажетті
көрсеткіштерді бере алады.Вариациялық
қатардың құрылымдық сипаттамасына:
мода, медиана, децили, квартили, перцентили
жатады.Мода деп – зерттелетін жиынтықта
басқаларына қарағанда жиі кездесетін
вариантаны айтады. Дискреттік қатарда
мода деп – көп рет кездесетін белгіні
айтады. Мода мысалы, сатып алушыларда
үлкен сұранысқа ие киім мен аяқ киімінің
размерін анықтау үшін жиі
қолданылады.Интервалды вариацияның
қатарда моданы есептеу үшін алдымен
мода орналасқан модальді интервалды
анықтау керек, ал одан кейін белгінің
модальді шамасының мәнін анықтау керек.
Медиана (Ме)- белгілі бір тәртіппен
орналасқан, өсуі бойынша немесе азаюы
бойынша реттелген қатардың варианттарының
бірінің орташасы. Ол мұндай қатарды
ортасынан бөледі. Медиананы табу үшін
реттелген қатардың ортасында орналасқан
белгінің мәнін табу керек. Тақ қатардағы
реттелген қатардың медианасы деп
ортасында тұрған белгінің шамасын
айтады. Тақ қатардағы реттелген қатардың
медианасы номері келесі формуламен
есептеледі: NMe=
,
мұнда
–
қатардың мүшесі саны; Жұп сандағы
реттелген қатардың медианасы деп
қатардың ортасында орналасқан екі
варианттың бірінің орташа арифметикалығын
айтады. Дискретті вариациялық қатардың
медианасы жиынтық көлемінің ортасынан
асатын жинақталған жиілігін сомасымен
табылады. Вариациялық қатардағы моданы
және медиананы тапқаннан кейін қатарды
4 бірдей, 10 және 100 бөлікке бөлетін
бірліктердің белгісі мәнің табуға
болады. Бұл шамаларды «децили», «квартили»,
«перцентили» деп атайды.
25.
Арифметикалық және өлшенген орта
шамалар, олардың қасиеттеріне тоқталыңыз.
Арифметикалық орта шама. Биологиялық
және ауылшаруашылық ғылыми – зерттеу
жұмыстарында көбінесе арифметикалық
орта шаманы табудың үлкен маңызы бар.
Өзінен оң және теріс ауытқуларының
қосындысы нөлге тең шама – арифметикалық
орта шама деп аталады. Мысалы 3 өсімдіктің
жемістерінің саны 4,5,6 болсын делік. Осы
3 өсімдіктердің жемістерінің орта шамасы
(4+5+6):3=6 болады. Осы орта шамадан 4=(-2)
,5=(-1) ,9=3 болып ауытқиды. Яғни оң және
теріс ауытқулардың қосындысы (-2)+ (-1)+3 =
0. Арифметикалық орта шаманы табу үшін
барлық вариантты қосады және оларды
бақылаулар санына бөледі. Вариациялық
статистикада арифметикалық орта шама
М немесе Х(икс покрытое ) арқылы
белгілейміз. Ариметикалық орта шаманы
табу үшін мына формуланы қолданамыз:
х=
немесе
М
=
.
Арифметикалық
орта шаманы осылайша есептеу тек
бақылаулар саны аз болғанда ғана немесе
электрондық есептеу машиналарын
пайдаланған кезде ғана қолданылады.
Варианттардың саны көп күрделі вариациялық
қатарларды өңдеген кезде арифметикалық
орта шаманы осылайша есептеу көп еңбек
сіңіруді қажет етеді. Сондықтан орта
шаманы есептеу үшін моменттер әдісі
немес кез келген бастама әдісі қолданылады.
Өлшенген орта шама. Практикалық және
ғылыми мақсаттар кейде біркелкі
материалды зерттеуден алынған бірнеше
орта шамаларды біріктіруді және осылайша
біріктіру негізінде зерттелген
материалдың бардығын сипаттай алатын
бір жалпы орта шама табуды қажет етеді.
Әрбір жеке орта шаманы табуға себепкер
болған бақылаулар санын оның салмағы
деп атайды. Алынған орташа өнім туралы
дұрыс түсінігіміз болу үшін біз өлшенген
орта шаманы есептеп шығаруымыз керек.
Яғни әрбір орта шаманы өзінің салмағына
көбейтіп,ол көбейтінділердің қосындысын
салмақтарын қосындысына бөлу керек.
26. Биометрияда мәліметтерді жазу ережелерін сипаттап, вариациялық қатарды құрыңыз. Биологиялық зерттеу зерзатын бірден бірнеше белгілері бойынша бақылау, олар жөнінде толық мағлұмат алып, жүргізілетін тәжірибе жұмыстарынын нәтижелігін арттыруға мүмкіндік береді. Зерттеу жүмыстарын жүргізу барысында алынған нақты мәліметтер күнделіктерге, протоколдарға, анкеталарға, дәптерлерге, бланкаларға және де басқа арнаулы құжаттарға тіркелеп отырылады. Бұлар нақты мәліметтер деп аталады. Мысалы, дала жағдайындағы зоологиялық, ботаникалық немесе мал шаруашылығы саласында жүргізілетін зерттеулерде алынатын нақты мәліметтерді, күнделіктер мен арнайы дайындалған қойын дәптерлеріне жазу ыңғайлы болса, зертхана жағдайында алынатын мәліметтер протоколдарға, журналдар мен бланкаларға толтырылады. Зерттеу барысында алынатын мәліметтерді есепке алу әдістері көп. Олар арнайы белгіленген әдістемелер бойынша алынып, рет-ретімен жазылып отырылуы тиіс. Биологиялық немесе ауыл шаруашылығы саласында жүргізілетін зерттеу жүмыстарында жинақталатын алғашқы мәліметтер, кездейсоқтық жолымен не¬месе арнайы қолданылатын әдістемелерге сай, қандайда бір заңдылықты сақтау арқылы алынуы қажет. Мысалы, белгілі бір мал тобын құрайтын жалпы жиынтықтан зерттеулерге қажетті шағын тобын кездейсоқ іріктеу жолымен бөліп алу, яғни шетінен кажетті мал санын бөліп алу немесе әрбір 10, 15, 20 малдан кейін бір бөлігін бөліп қалып отыру жолымен алынса, дала отының қүрамы мен құнарлығын анықтау жүмыстары өзіндік әдістемелерге сай келісілген шаршы метр көлемін кездейсоқ тандап алып, сол жерде өсетін барлық шөптердің түрлері мен масса қүрамын анықтау арқылы атқарылады. Мұнда зерттеу жүмыстарында қолданылатын әдістемелердің дүрыс таңдап алы¬нуы басты назарда болуы қажет.
27. Вариациялық қатар түрлері мен оларды құрудың жолдарын көрсетіңіз. Вариациялық қатардың екі түрі болады: жай және күрделі. Жай вариациялық қатар – деп әр вариантасы тек біреуден ғана болып келетін вариациялық қатард айтамыз, ал күрделі вариациялық қатар – деп әр вариантасы бірнешеу болып келетін вариациялық қатарды айтамыз. Вариациялық қатар құру үшін варианттарды өсу тәртібімен орналастырамыз. Онан соң варианттарды тарта отырып алнған іріктеуде әр бір варианта қанша рет кездесетіндігін анықтаймыз. Вариациялық қатар туралы түсінік Сапалық белгілерді зерт- тегенде әдетте әр түрлі белгілері бар өкілдерді санап, олардың жалпы топтағы үлесін пайыз арқылы көрсетеді. Мысалы жылқы үйіріндегі қара, торы, күрең түсті биелер немесе сары, жасыл түсті бұршақтар үлесі және т.б. Бүған керісінше, сандық белгілері арқылы бір топ малды сипаттау қиындау, себебі ол белгілердің мәндері әр түрлі болып келеді. Сондықтан оларды шартты түрде белгі мөлшеріне (өлшемдеріне) қарап топтарға (кластарға) бөледі, яғни вариациялық қатар қүрады. Мұнда әрбір топта неше өкілдің бар екендігі қөрсетіледі. Вариациялық қатар деп белгілердің мөлшеріне қарай олардың өкілдерінің топтарға ретті түрде орналасуы айтылады. Ва- риациялық қатар екі көрсеткіштерден тұрады; біріншісі топтар (кластар) аралықтары, екіншісі олардың сәйкес жиілігі (саны). Вариациялық катар ең кішкене шамадан ең көп санды белгілерге дейінгі мәндердің құбылуын, әрбір топтағы вариант жиілігін (са- нын) көрсетеді. Вариант саны ең көп кездесетін топ модалъдық деп аталады. Басқаша айтқанда, ең жиі кездесетін белгілер бар топ модалъдық класс деп аталады. Вариациялық қатар құру тәртібі. Зерттеулер нәтижесінде алынған көрсеткіштерді биометриялық жолмен өңдеу жұмыстары жинақталған мәліметтерді екшелеп, вариациялық қатар құрудан басталады.
28. Вариациалық қатардың санын және класс көлемін анықтаудың ережелерін атаңыз. Күрделі вариациялық қатар құрумен қатар, гистограмма сызыңыз. Зерттеуден алынған мәліметтерді талдау кезінде, егер өзгергіштіктің шайқалу шегі үлкен болса варианттарды кластарға жіктеу керек. Мысалы, бір түрге жататын балықтардың уылдырықтарының саны олардың жас ерекшеліктеріне қарай бір-бірінен 500-ден аса данаға дейін айырмашылық беруі мүмкін. Бұл варианттардың барлығын бір бағана етіп жазу мүмкін емес.
Үзіліссіз өзгергіштіктерде варианттар көп жағдайда аралас сандар болып келеді, мысалы өсімдіктің биіктігі: 1,25; 2,15; 3,45; м т.б. Бидай дәніндегі белоктың мөлшері - 15,2; 16,1; 16,5% т.б. Екі бүтін сандар арасында 0,01 немесе 0,01%-ке өзгешеленетін 100 варианттар орналаса алады.
Осы сияқты жағдайларда варианттар кластарға жіктеледі, ол үшін мынадай ережелерді ескеру керек:
Кластардың шекарасын аиықтаған кезде, эр варианта бір ғана класқа кіретін болуы керек: мысалы 5-9, 10-14, 15-19 т.б. Кластарды ешуақытта 5-10, 10-15, 15-20 деп бөлуге болмайды.
Барлық кластардың мөлшері бірдей болуы керек.
Бірінші жөне ақырғы кластар толық болмауы мүмкін. Мысалы, егер кластың мөлшері 10, ал өзгергіштіктің шайқалу шегі 76 болса, 77-79 варианттарының жоқтығына қарамастан ақырғы кластың мөлшері 70-79 болады.
Кластардың саны 6-7-ден кем, 10 -15-тен артық болмауы керек.
Кластардың мөлшерін анықтау үшін максимум жене минимум варианттарды табады, одан соң өзгергіштіктің шайқалу шегін анықтайды жөне оны белгіленген кластардың санына бөледі, алынған санды бүтін санға дейін дөңгелектейді. Мысалы, жүгері сабақтарының биіктігі өлшенді:
Рет тік № |
Биік тігі |
Рет тік № |
Биік тігі |
Рет тік № |
Биік тігі |
Рет тік № |
Биік тігі |
Рет тік № |
Биік ТІІІ |
1 |
132 |
14 |
131 |
27 |
131 |
40 |
103 |
53 |
128 |
2 |
160 |
15 |
128 |
28 |
173 |
41 |
126 |
54 |
124 |
3 |
100 |
16 |
136 |
29 |
133 |
42 |
143 |
55 |
108 |
4 |
155 |
17 |
125 |
30 |
110 |
43 |
141 |
56 |
132 |
5 |
126 |
18 |
144 |
31 |
152 |
44 |
125 |
57 |
143 |
6 |
129 |
19 |
118 |
32 |
144 |
45 |
154 |
58 |
147 |
7 |
125 |
20 |
138 |
33 |
147 |
46 |
116 |
59 |
131 |
8 |
106 |
21 |
123 |
34 |
138 |
47 |
105 |
60 |
154 |
9 |
164 |
22 |
134 |
35 |
131 |
48 |
133 |
61 |
102 |
10 |
114 |
23 |
118 |
36 |
166 |
49 |
142 |
62 |
157 |
11 |
127 |
24 |
179 |
37 |
132 |
50 |
141 |
63 |
113 |
12 |
163 |
25 |
153 |
38 |
114 |
51 |
115 |
64 |
123 |
13 |
111 |
26 |
116 |
39 |
133 |
52 |
144 |
|
|
Бақылау саны n= 64.
Өзгергіштіктердің шайқалу шегі 179-100=79 см. Егер біз класс мөлшерін 10 деп алсақ, онда 79: 10=8 класс болады. Енді осы кластардың шекараларын белгілейміз және вариациялық қатар құрамыз.
Кластар |
Жиілік |
Ғ |
100-109 |
|
6 |
110-119 |
|
10 |
120-129 |
|
12 |
130-139 |
|
14 |
140-149 |
|
10 |
150-159 |
|
6 |
160-169 |
|
4 |
170-179 |
|
2 |
Кластарға жіктелген вариациялық қатарды график арқылы бейнелсу гистограмма деп аталады. Гистограмма жасаған кезде горизонталь осьтің бойына кластардың мөлшерін, ал вертикаль осьтің бойына жиіліктерді орналастырады. Гистограмманы вариациялық қисыққа айналдыруға болады. Ол үшін кластардың ортасын түзу сызықтармен қосу керек.
29. Биологиядағы математикалық - статистикалық тәсілдердің рөлін сипаттап, жиынтықты статистикалық талдаудан өткізіңіз. Материалды статистикалық өңдеудіңнегізгі мақсаттарының бірі- тәжірбиеден алынған жиынтықтардың өздеріне тән ерекшеліктерін сипаттайтын көрсеткіштіктерін табу және оларды бір бірімен салыстыру болып табылады. Статистикалық жиынтықтарды екі көрсеткіш жеткілікті, толығырақ сипаттай алады:1. Белгінің орташа мөлшері; 2. Өзгергіштік немесе шашырап бытырау дәрежесі. Жекелеген элементтердің сипаттық құрамы негізінде тұтас бір түр немесе популяцияған тән ортақ белгілер жөнінде белгілі бір тұжыымға келуге болады. Популяция шеңберінде белгілер көрсеткіштері ауытқығанымен, олар белгілі дәрежеде зерттелетін обьектінің ортақ заңдылықтарына бағынады. Зацдылық белгілі бір көлемдегі (сандағы, мөлшердегі, өлшемдегі т.б.) белгілердің ортақ көрсеткіштеріне негізделеді. Қандай да бір құбылыс жөнінде пікірге келіп, оның тұрақты түрде қайталанатынына көз жеткізетін болсақ - заңдылық деп қарастыруға негіз болады. Көлемі (саны) неғұрлым үлкен жиынтықтарды зерттеу нәтижесінен анықталған заңдылықтың, мәні солғұрлым шынайырақ келеді.
Заңдылықты жекелеген құбылысты ғана емес, көптеген құбылыс жиынтықтарын сараптау нәтижесінде анықтауға болады. Биометриялық статистикадағы зерттелетін белгілердің нысаны - жалпы сапалық негізбен бірлескен, біртектес, бір-бірінен тәуелсіз жеке бірліктері, яғни өзгермелі көптеген бірліктерден тұратын жиынтықтардан құралады. Жиынтық жеке бірліктерден немесе мүшелерден түрады. Жиынтық деп мысалы, бір тұқымға жататын мал тобын, бір атадан немесе анадан тараған топты немесе зерт¬теу жүргізілетін өсімдіктер тобын (түқым, сүрып) айтуға болады. Бір үйір жылқы үшін бірлік мүшесі әрбір жекеленген жылқы болып табылады. Жиынтық бірлігі белгілерімен сипатталады.
Егер бір немесе бірнеше мәнді белгілер барлық белгілер үшін бірдей болса, онда зерттелетін жиынтық біртекті болып саналады. Әр түрлі типтегі құбылыстардан тұратын жиынтық - әр текті болып табылады. Зерттеу үшін алынған белгілі бір жиын- тықтардың қүрастырушы бөліктерін жиынтың бірліктері деп атайды.
Белгілерді зерттеу белгілі бір көлемдегі жиынтықта жүзеге асырылады. Биометриялық статистикада есептеулер жүргізу үшін популяция көлемінде алынатын жалпы жиынтық және іріктелген жиынтық деп бөледі.
Жалпы жиынтық деп зерттелуге алынған зерзатының барлық көлемі, мысалға алғанда бір тұқымға жататын барлық жылқылар немесе қойлар жиынтығы айтылады. Жалпы жиынтыққа мәселен бір мал тұқымынан алынған қанның қызыл не ақ түйіршіктерінің жалпы саны да жатады. Жалпы жиынтыққа кейде бірнеше мыңға дейін мал басы кіруі мүмкін. Түқым көптеген жиынтыққа ажырайды, популяциялық топтарға, жеке мал отарларына, аталық желілерге (линия), аналық ұяларға (семейство) және т.б.
Жалпы жиынтықты тұтастай есепке алып, сипаттау өте көп әрі күрделі жүмыс болғандықтан, биометриялық есетеулер барысында одан ішінара іріктелген бір бөлігін (тобын) ғана зерттейді. Көптеген тәжірибелер көрсеткендей ішінара іріктелген жиынтық нәтижелері жалпы жиынтықтың құрылымына сәйкес келіп, оны сипаттауға мүмкіндік бере алады. Бірақта, алынған мәліметердің жалпы жиынтықтың мәндеріне толықтай дәл келуі мүмкін емес. Іріктеу нәтижелері жалпы жиынтықтың көрсеткіштеріне мейлінше сәйкес келуі үшін, зерттеу мақсатында белгілі бір жиынтықтан іріктелетін әрбір мүше кездейсоқ алынуы керек. Тек сонда ғана ішінара іріктеу жалпы жиынтық жөнінде дұрыс мағлұмат алуға мүмкіндік береді, яғни ол - репрезентативті болады. Егер іріктеуге 30 мүшеге дейін кірсе (п<30) ол кіші іріктелген жиынтық, ал 30-дан көп болса (п >30) үлкен жиынтық деп аталады.
30. Белгілердің әртүрлілік көрсеткіштеріндің сипаттамасын беріңіз. Зерттеу үшін алынған әрбір жеке жиынтықтардың жекелеген даналары орта мөлшерден әр дәрежеде ауытқиды, сондықтан зерттелуге тиісті іріктеуді сипаттау үшін тек арифметикалық орта шаманы табу жеткіліксіз. Мүндайда осы әртүрлілік дәрежесін сипаттай алатындай көрсеткіштер келтіру керек. (Бірсыпыра оқулықтарда “белгілердің әртүрлілігі” деген сөздің орнына “бытырау”, “өзгеру” деген терминдер қолданылады).
Белгілер әртүрлілігінің керсеткіштері қызметін лимиттер өзгергіштіктің шайқалу шегі, орташа квадраттық ауытқу б (сигма), варианта б2 жөне вариация коэффициенті С.v. атқарады. Әртүрлілік көрсеткіштерінің бәріне тән жалпы қасиет олар осы саналуан әртүрлілік ерекшеліктерінің қандай дәрежесі болса да нақты белгілей алады.
Н.А.Плохинский мынадай мысал келтіреді. Екі совхоздағы огіздердің салмағын зерттеуден мынандай мәліметтер алынды.
Өгіздердің реттік № |
1 – совхоз |
2 – совхоз |
|
Тірі салмағы кг |
|
1 |
640 |
600 |
2 |
645 |
630 |
3 |
650 |
650 |
4 |
655 |
680 |
5 |
660 |
700 |
Өгіздердің тірі салмағы екі совхозда да орта есеппен бірдей – 650 кг-нан; бірақ өгіздердің салмақтарының әртүрлілігі екінін совхозда бірінші совхозға қарағанда 5 есе көп. Осы әртүрлілік лимиттер мен өзгергіштіктің шайқалу шегі арқылы көрсету қолайлы болып шығады.
Lim1 = 640 – 660 кг (20кг)
Lim2 = 600 – 700 кг (100 кг)
Бірталай жағдайларда топтардың әртүрлілігін лимиттер мен өзгергіштіктің шайқалу шегі арқылы көрсетудің үлкен өндірістік маңызы бар, олар белгілі бір продукцияға ақша төлеу үшін негіз етіп алынады. Мысалы, қақталып тұздалған тұтас еттің бір партиясының М1 = 90 кг, lim1 = 88-92 (4кг), ал екіншісінің М2 = 90 кг, lim2 = 80-100 (20) кг болсын делік. Әрине, бірінші партияның еттері екіншісіне қарағанда стандарт ретінде жоғары бағаланады.