54.Белгілердің корреляциялық байланысын сипаттап, салыстырмалы талдау жүргізіңіз.

Корреляция латынның correlation деген сөзінен шыққан. Ол өзара бір бірімен байланыстылық,қатынастылық,тәуелділікті көрсетеді. Биологиялық зерттеулер кезінде бір организмнің белгілері арасындағы байланыстарды немесе организнің белгілермен сыртқы орта жағдайларының арасындағы тәуелділікті тексеру қажеттігі жиі кездеседі. Тірі обьектілерді – өсімдіктерді ,жануарларды,микроорганизмдердізерттеген кезде ,олардың белгілері арасындағы байланыс тек корреляция немесе корреляциялық байланыс ретінде ғана байқалады. Онда бір белгінің әрбір мәнінде басқа белгінің бірнеше мәндері ,яғни оның таралуы дәл келеді.Мысалы адамның биіктігі мен салмағы арасында байланыс бары белгілі. Бірақ биіктігі бірдей адамдардың салмағы бірдей болмай,55; 60; 65 кг шегінде өзгере алады. Сондықтан корреляциялық байланысты зерттеудәі мәнісі жекелеген белгілер арасындағы немесе белгілердің дамуымен орта жағдайлары арасындағы байланыстың сипатын және байланыстың қаншалықты тығыз екендігін анықтау болып табылады. Корреляциялық байланыстарды зерттеу үшін зерттелетін материалға жан –жақты сапалық анализ жасаудың шешуші маңызы бар. Мысалы , тұқымдағы белоктың мөлшері мен өсімдіктердің өсу жағдайларының арасындағы тәуелділікті зерттеу керек болсын деп есептелік дедік. Ол үшін бір сорттың үлгілерін әртүрлі,бірақ белгілі жағдайларда өсіріп,олардың әрқайсысынан белгілі бір көрсеткіштер алу керек те,сол көрсеткіштерді бір бірімен салыстыру керек. Мысалы, егер біз Безостая –І қыстық бидайды тұқымындағы белоктың мөлшерін азот тыңайтқыштарын қолдануға тәуелді екенін анықтағымыз келсе, онда тек азот тыңайтқыштарының берілу дозасын ғана өзгерту керек те басқа жағдайлардың бәрі бірдей болу керек. Корреляциялық тәуелділікті есептеуге кіріспестен бұрын зерттелетін құбылыстар арасында байланыстың болу немесе болмау мүмкіндігін талдап қарастыру керек,олай болмаған жағдайда қате нәтижелер алынуы мүмкін.

55. Күрделі корреляциялық байланыстың сызба - нұсқасын көрсетіңіз.Корреляция латынның correlation деген сөзінен шыққан. Ол өзара бір бірімен байланыстылық, қатынастылық, тәуелділікті көрсетеді. Биологиялық зерттеулер кезінде бір организмнің белгілері арасындағы байланыстарды немесе организнің белгілермен сыртқы орта жағдайларының арасындағы тәуелділікті тексеру қажеттігі жиі кездеседі.Тірі обьектілерді–өсімдіктерді, жануарларды, микроорганизмдерді зерттеген кезде, олардың белгілері арасындағы байланыс тек корреляция немесе корреляциялық байланыс ретінде ғана байқалады. Онда бір белгінің әрбір мәнінде басқа белгінің бірнеше мәндері, яғни оның таралуы дәл келеді. Корреляциялық тор жасау үшін зерттелмекші болып отқан әрбір обьект бойынша көрсеткіштер белгілі тәртіппен жазылуы қажет. Мысалы, өсімдік жапырақтарының санымен оның биіктігі арасындағы байланысты зерттеу керек болса. Біз екі көрсеткіш бойынша (Жапырақтарының саны-у , және өсімдік биіктігі -х) мәліметтер жинадық.Вариациялық қатарлар құрамыз : оның біреуін горизонталь , екіншісін вертикаль бағытта орналастырамыз. Өсімдік биіктігінің (х-қатары) ең кіші көрсеткіші 9, ең үлкені 18. Жапырақтар санының (у-қатары) ең кіші көрсеткіші 3 , ең үлкені 12. Өзгергіштіктің шайқалу шегі екі қатарда да бірдей 9 –ға тең , демек, варианттарды кластарға жіктеудің қажеттілігі жоқ.Корреляциялық тор құрамыз. Варианттарды тор ішіне таратамыз. Ол үшін жиілікті статистикада қолданылатын нүктелеер арқылы белгілейміз.Бірінші өсімдіктің биіктігі 15 cм, ал жапырақтарының саны 9 болғандықтан 15 –ші графамен 9 –шы графаның қиылысқан жеріне нүкте қоямыз. Екінші өсімдіктің биіктігі 10 см , жапырақтарының саны 6. Сондықтан келесі нүктені 10 –шы графамен 6 – шы графаның қиылысқан жеріне қоямыз т.б. Тарату аяқталған соң нүктелерді цифрлармен ауыстырамыз. Горизонталь және вертикаль бағаналары бойынша бақылаулар саны қосындысын, одан соң олардың жалпы қосындысын табамыз. Мысалда, қосынды вертикаль бағана бойынша да, горизонталь бағана бойынша да 30 – ға тең, яғни тәжірибе үшін алынған өсімдіктер санына дәл келеді. Шартты орта шамалар етіп х қатары 14 – ті, ал у қатары үшін 7 – ні аламыз. Шартты орта шамадан ауытқуларды есептейміз де оларды a_x және a_y деген тарауларға жазамыз. Шартты орта шамаларды қоршап шектейтін сызықтар арқылы тор төрт квадрантқа бөлінген. Оларды І, ІІ, ІІІ, ІV рим цифрларымен белгілейміз. Бірінші Х катары бойынша, сосын У қатары бойынша түзетпе мен ауытқуды тауып аламыз. Сосын корреляция коэффициенті мен корреляция қатесін табамыз.в= ;

r = m_r = .

56. Мода және медиана көрсеткіштері. Орташа квадраттық ауытқуды (сигма) Гаусс ұсынған формуламен есептеңіз. Белгінің сандық көрсеткіші варианта немесе дата деп аталады және vнемесе x– пен белгіленеді. Варианттардың төменнен жоғарыға өсіп немесе жоғарыдан төменге кеміп орналасу тәртібі вариациялық қатар құрайды. Вариациялық қатар құру үшін максимал жіне минимал варианттар табылады да, олар белгіленеді. Біздің мысалымызда минимал варианта 12, максимал варианта 20. Минимал варианта мен максимал вариантаның арасындағы айырма өзгерудің тербелу өрісі немесе өзгергіштіктің шайқалу шегі деп аталады. Вариациялық қатарды графика арқылы бейнелеу вариациялық қисық деп аталады. Вариациялық қатардағы ең көп кездесетін вариантаны мода деп атайды. Біздің анықтауымызда мода 15 – тең. Вариациялық қатардың ортасында орналасқан варианта медиана(лат. орталық)деп аталады. Мода Мо, ал медиана Ме белгілерімен белгіленеді. Белгілі математик Гаусс әртүрлілік дәрежесінің көрсеткіші ретінде негізгі ауытқуды пайдалану керектігін ұсынды. Ол орта шамадан ауытқулар квадраттарымен жиіліктердің көбейтінділерінің қосындысын бақылаулар санына бөліп квадрат түбірін тапқанда шыңатын санға тең, яғни,

  .   Оң және теріс ауытқулардың (орта шамадан ) қосындысы нөлге тең болатыны белгілі. Ауытқуларды квадратқа дәрежелегенде барлық таңбалар оң, демек олардың қосындылары да оң шама болып шығады. Кейбір жекелеген жиынтықтар шамаларының әсерін жоғалту үшін ауытқулар квадраттарымен жиіліктер көбейтінділерінің қосындысын бақылаулар санына бөледі. Кейінірек Гаусстың формуласы азырақ өзгертілді: жоғарыда келтірілген формуладағыдай ауытқулар квадраттармен жиіліктерінің көбейтіндісінің қосындысын бақылаулар санына (п) емес, ерікті дәрежелер санына (п-1) бөлу керек деп табылды. Ерікті дәрежелер саны тәуелсіз шамалар санына тең болады. Мысалы, егер екі санның қосындысы 10, ал қосылғыштардың біреуі 3-ке тең болған жағдайда, екінші сан тек 7 болуы ғана керек. Егер қосынды үш саннан тұрса, онда оның екеуі тәуелсіз болады да, үшіншісі бірінші екі санның қосындысымен анықталады.Сондықтан ерікті дәрежелер саны п-1 –ге тең болады. Сонымен Гаусстың формуласы енді былайша өрнектеледі: . Ерікті дәрежелер саны v деген грек алфавиті мен немесе df деген екі латын алфавитімен белгіленеді. Квадраттық немесе негізгі ауытқуды есептеу үшін вариациялық қатар құрылады. Вариациялық қатардың ортасында орналасқан бір вариантты шартты орта шама етіп алады да,сол орта шамадан ауытқуларды табады және ауытқуларды өзінің жиіліктеріне көбейтеді; онан соң ауытқулармен жиіліктердің көбейтіндісінің алгебралық қосындысын табады да ол қосындыны бақылаулар санына бөлу арқылы түзетуді табады. Сонан соң ауытқулардың квадратын жиіліктерге көбейтіп, оларды қосады және ауытқу квадраттары мен жиіліктер көбейтіндісінің қосындысын ерікті дәрежелер санына бөледі және одан түзетудің квадратын алып тастайды да, шыққан санның квадрат түбірін табады. Орта шама қандай бірліктермен белгіленсе негізгі немесе квадраттық ауытқуда сол бірліктермен белгіленеді. Сондықтан да ол әр уақытта атаулы сан болып табылады. Өзгергіштіктің шайқалу шегі неғұрлым аз болса, сигманың мәні де соғұрлым аз болады. Егер өзгергіштік жоқ болса сигма=0. Тірі организмдер салмағы, биіктігі және басқа көрсеткіштері бойынша айтарлықтай әртүрлі, сондықтан сигманың абсолюттік мәні кең көлемде өзгере алады.

57. Молденгауэр факторын қолданып арифметикалық орташа шаманың қателігін есептеуді көрсетіңіз. Варианттары көп, ал қайталанылу саны азырақтау тәжірибе мәліметтерін өңдеген кезде арифметикалық орта шаманың қатесңн жеңілдеу жолмен де есептеп шығаруға болады. Ол үшін Молденгауэр факторын (констант К) пайдалана отырып мына формула бойынша есептейді: m = ║ a║ * K.Мұнда ║ a║ - таңбадан тәуелсіз ауытқулардың қосындысы, ал К-мына формула: К = 1/ 0.79788*√n–1 бойынша есептеп шығарылған, қайталанулардың санына қарай өзгеріп отыратын константа. П.Н. Константиновтың ‘‘Дала тәжірибелер методикасы’’ кітабында орта шамалардың қателер үшін К-константалары кестесі келтірілген. Қайталанулар саны көп болған жағдайда қателіктерді жеңілдеу жолмен есептеу көп уақыт үнемдеуге көмектеспейді. Мысалы әртүрлі микроэлементтердің әртүрлі дозасының бидай өнімділігіне тигізетін әсерін зерттедік дейік. Бізде тәжірибенің 40 варианты болды. Әр варианта 4 рет қайталану арқылы сыналды.Тәжірибенің бірінші вариантының мынадай өнім алынды.

Орта шаманың және ауытқулардың дұрыс есептелгендігін тексеру үшін біз алдымен оң және теріс ауытқулардың қосындысын табамыз: -0,6 + (-0,8)=-1,4 +0,8+0,6=+1,4. Бұл есептеулер тек тексеру үшін ғана керек және келешектегі есептеулерге ешқанда қатыспайды. Оң және теріс ауытқулардың қосындысы бір-біріне тең, демек есептеулер дұрыс жасалған. Ауытқулардың таңбасына қарамай қосындысын табамыз, сосын 4 қайталану үшін берілген 0,1809 тең константаға көбейтеміз. 3,0 * 0,1809 = 0,5427 Орта шама 26±0,54 ц.

58. Арифметикалық орта шамалар арасындағы айырманың сенімділігін және нөлдік гипотезаны сипаттаңыз.Әрбір тәжірибенің түпкілікті мақсаты зерттелуші тәжірибе варианттарының арасында сенерліктей айырмашылықтардың бар немесе жоқ екендігін дәлелдеу болып табылады. Мысалы: өндірісте егіліп жүрген сорттармен селекционердің жаңадан алған саорттарының өнімділіктері арасындағы айырмашылық, берілген тыңайтқыштар әсерінен дақылдар өнімділігінің өзгеру айырмашылығы, өсімдіктер мен жануарлар түрлерінің арасындағы сандық көрсеткіштер т.б. Іріктеулер үшін табылған арифметикалық орта шамалардың өзгеріп отыратындығы соншалық, оның қанша мөлшерге өзгеретіндігін көрсету үшін, әрбәр отра шамамен оның қатесін де табу керек: m. Екі орта шама арасындағы айырманың сенімділігін сол айырманың өз қатесіне қатынасы арқылы анықтайды. Айырманың қатесі қателіктер квадраттарының қосындысынан табылатын квадраттық түбірге тең: . Мысалы, ылғалдың жетіспеушілігі жағдайларында жаздық бидай өнімділігіне фосфор тыңайтқыштарының әсерін зерттеу тәжірибесінен мынадай мәліметтер алынды. Контроль (тыңайтқышсыз) -11,5 ± 0,2 ц/га. Суперфосфатпен өңдегенде -13,1±0,3 ц/га. Орта шамалар арасындағы айырманы анықтаймыз: 13,1-11,5 = 1,6 ц/га. Айырманың қатесін есептейміз: Айырманың өз қатесіне қатынасын табамыз: 1,6:0,36 = 4,4. Биометрия бойынша ескі оқу құралдарында, егер бұл қатынас 3-ке немесе одан да көбірекке тең болса, айырма сенімді деп көрсетіледі. Ал, қазір одан да ділірек, айырманың сенімділігі стьюдент критериі t-мен анықталады; t-айырманың өз қатесі қатынасына тең,t = . Демек, ерікті дәрежелер саны υ = 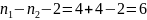. Ерікті дәрежелер саны 6, 0,95 ықтималдылықта t-ның сенімділігі 2,45-ке тең, 0,99 ықтималдылықта t-ның сенімділігі 3,71 тең. Демек, контроль және тәжірибе варианттары өнімдері арасындағы айырма 0,99 ықтималдылықтан да жоғары деңгейде сенімді.

59.Белгінің қалыпты таралу заңдылықтарын, қисық сызықты талдаңыз.Талдау кезінде әдетте зерттеуші көп санды мәліметтер алады. Гистограммалар мен вариациялық қисықтар құру сол алынған көп санды мәліметтердің мәнін түсінуге және олардан қандай да болмасын бедгеле заңдылық табуға көмектеседі. Графиктер көбінесе баспа жұмыстарында және ғылыми зерттеу жұмыстарында және ғылыми зерттеу жұмыстары бойынша жазылатын отчеттарда жиі орын алады. Салыстыруға ыңғайлы болу үшін бір чертежда кейде бірнеше сызықтар беріледі. Әрбір чертежде тәжірибенің варианттары қалай бейнеленгенін көрсететін экспликация болуы керек. Көптеген ауылшаруашылық және биологиялық обьектілердің белгілері үшін ол белгілердің қалыпты таралуы тән, яғни белгілердің жекелеген варианттары мөлшері неғұрлым орта шамадан алшақтаған сайын, ол вариант соғұрлым сирек кездесетін болады. Мысалы, көпшілік адамдар орта бойлы. Алып адамдар (биіктігі 200 см-ден артық болатын) және өте аласа адамдар (биіктігі 100 см-ден кем) өте сирек кездеседі. Бірқалыпты тарап бөліну белгілерге тән қасиет болғанымен кейде одан ауытқулар да кездеспей қоймайды. Жиі кездесетін осындай ауытқымалы таралуларға қисаю (ассиметрия), тіп-тіке шыңды (эксцесс), екі шыңды және көпшыңды тарап бөлінулер жатады. Екі және көпшыңды қисықтардың пайда болуының ең басты себебеі – зерттеу үшін алынған материалдың біркелкі болмауы. Биометрия ғылымы жаңадан пайда бола бастаған кезде Голландия ғалымы Гуго де-Фриз алқа тұқымдастарына жататын Энотера ламаркина өсімдіктерінің күлте және тостағанша жапырақтарының ұзындығын өлшеп биометриялық зерттеу жасады. Осы зерттеулердің нәтижесінде Ф. Гальтон жұмыстарындағыдай біршыңды қалыпты қисықтар күтілген еді, бірақ оның орнына екі жағдайда да екі шыңды немесе бимодальді қисықтар алынды. Тәжірибе үшін алынған өсімдіктерді толық зерттей келіп, ол Энотера Ламаркиана түрінің бір–бірінен жақсы өзгешеленетін екі түрден – кәдімгі энотера ламаркиана мен энотера Гиганстан тұратындығын тапты. Парктикалық жұмыстарда кейде жекелеген варианттардың жиілігі кенет көтеріоіп немесе төмендеп кететін жағдайлары байқалады. Қисықтың осындай шығыңқы жері қателіктер протуберанциясы деп аталады. Олардың пайда болу себептері: зерттелуші обьектілердің санының жетіспеуі; зеттелуші белгілердің тым ұсақ градациялануы; санағанда немесе өлшеген кезде жіберілген қателіктер.

60.Корреляция туралы ұғымды және корреляция коэффициентін есептеңіз. Корреляция латынның correlation деген сөзінен шыққан. Ол өзара бір бірімен байланыстылық, қатынастылық, тәуелділікті көрсетеді. Биологиялық зерттеулер кезінде бір организмнің белгілері арасындағы байланыстарды немесе организнің белгілермен сыртқы орта жағдайларының арасындағы тәуелділікті тексеру қажеттігі жиі кездеседі. Тірі обьектілерді – өсімдіктерді, жануарларды, микроорганизмдерді зерттеген кезде, олардың белгілері арасындағы байланыс тек корреляция немесе корреляциялық байланыс ретінде ғана байқалады. Онда бір белгінің әрбір мәнінде басқа белгінің бірнеше мәндері, яғни оның таралуы дәл келеді. Мысалы адамның биіктігі мен салмағы арасында байланыс бары белгілі. Бірақ биіктігі бірдей адамдардың салмағы бірдей болмай, 55; 60; 65 кг шегінде өзгере алады. Сондықтан корреляциялық байланысты зерттеудің мәнісі жекелеген белгілер арасындағы немесе белгілердің дамуымен орта жағдайлары арасындағы байланыстың сипатын және байланыстың қаншалықты тығыз екендігін анықтау болып табылады. Корреляцияда бір көрсеткіш өскен сайын екінші көрсеткіш те өсіп отырса немесе керісінше, бір көрсеткіш кеміген сайын екінші көрсеткіш те кеміп отырса, ондай коореляция түзу немесе оң деп аталады. Егер бір көрсеткіш өскен сайын екінші көрсеткіш азайса немесе бір көрсеткіш азайған сайын екінші көрсеткіш көбейсе ондай коррреляция кері немесе теріс деп аталады. Мысалы бір ұядағы жүгері өсімдігінің саны көп болған сайын собықтары кішкентай болады. Егер бір көрсеткіштің өсуіне қарай екінші көрсеткіште бірқалыпты өсіп немесе кеміп отырса, онда екі корреляция да түзу сызықты деп есептеледі. Егер бір көрсеткіш белгілі бір шекті мөлшерге дейін өскенде екінші көрсеткіште өсіп, соңынан кеми бастаса онда екі корреляцияда қисық сызықты корреляция деп саналады. Мысалы, белгілі жағдайда себі нормасын белгілі мөлшерге дейін көбейту егін өнімділігін арттырады,ал,себу нормасын одан әрі өсіру өсімдік аралығын жиілетеді де, егін өнімділігін кемітеді.Корреляция коэффициенті. Жоғарыда көрсетілген өсімдіктердің шоқ түптенуі мен салмағының арасындағы тәуелділіктің жеңілдетілген мысалдарын қарастырайық. Екі қатар бойынша да орта шамадан ауытқуларды есептейміз. Ауытқулар а_х және а_у арқылы белгіленеді. Әртүрлі қатарларды салыстырған кезде жұптанған ауытқулар көбейтінділері қосындысының сандық мәні орта шамаға қарағанда өзгеріп отырады. Сондықтан бұл тәуелділік өзін салыстырмалы сандар арқылы көрсетуді қажет етеді; ол үшін алынған қосындысы тұрақты және ең көп санға бөлу керек. Ал сан геометриялық орта шама (G) болып табылады, яғни ол түбір астындағы n санды даталар көбейтінділердің n дәрежелі түбірін тапқанға тең. Бірінші мысал. Екі қатар бойынша орта шамадан ауытқуларды квадратқа өсіреміз және оларды қосамыз. Х қатары: х 16; 4; 4; 16; 40. У қатары: у 64; 16; 16; 64; 160. Геометриялық орта шама G= = = 80. Корреляция коэффициенті r = = = 1. Теріс корреляция кезінде r = =-1. Корреляция жоқ кезде (3-ші мысал) r= = 0 т.б. Бұл формула шағын қатарлардан корреляция коэффициентін есептеу үшін пайдаланылады. Корреляция коэффициентін үлкен қатарлардан табу үшін осы формула басқаша түсіндіріледі. Квадраттық ауытқу (б) квадрат түбір астындағы ауытқулар квадраттарының қосындысын бақылаулар санына бөлгеннен кейін шығатын түбірге тең екенін біз бұрыннан білеміз: осыдан, және . Демек, *x= және *у= . Енді *x және *у мәндерін өз орындарына қойсақ мынадай формула аламыз: r = = . Күрделі вариациялық қатарлар үшін бұл формулаға жиілік мәні f кіргізіледі. Бұл белгілі Браве формуласы: r = . Шартты түрде алынған орта шамадан ауытқуларды есептеген кезде бұл формула мынадай болып өзгереді r =  b- түзету. Бақылаулар саны көп болған жағдайда корреляция коэффициентін осы формула бойынша тікелей есептеу бір сыпыра қиындық келтіреді және ол корреляциялық тор жасауды қажет етеді.Корреляциялық тор жасау үшін зерттелмекші болып отқан әрбір обьект бойынша көрсеткіштер белгілі тәртіппен жазылуы қажет.Мысалы, өсімдік жапырақтарының санымен оның биіктігі арасындағы байланысты зерттегіміз келсе, жазылу тәртібі төмендегідей болған жөн.