53.Биологияда бөліктер және хи – квадрат көрсеткіштерінің есептеу жолын мысалмен көрсет

К.Пирсон хи- квадрат әдісінің негізін қалады. Бұл әдіс арқылы түрлі

материалдар мен мақсаттарға сәйкес, белгілі бір сандық және үлестік мәнде көрсетілген қандай да бір гипотезалардың дұрыстығын тексеруге болады. Хи квадрат әдісі арқылы нақты тәжірибелер нәтижесінде алынған белгілер жиіліктерінің , гипотеза бой/ша болуы тиіс жиіліктерінен ауытқуларының шынайылық дәрежелері анықталады да , яғни генетикалық заңдылықтарды немесе жорамалдарды тексергенде оларға статистикалық дұрыс қорытындылар жасау үшін пайдаланылады.

Ол үшінкелесі формулалар қолданылады :

Статистикалық болжамдарды тексеру үшін келісім критерийлер

қолданылады, яғни ұсынылған болжамдарды қабылдап алу немесе қабыл

алмауға мүмкіндік беретін ережелер қолданылады. Нормальдық үлестірімнің

таңдама үлестірімге сәйкестігін ең жиі тексереді, өйткені нормальдық

үлестірім жиі кездеседі. Үлестірім туралы келісім критерийлерінің

жиынынаң ең қуатты деп саналатын (хи квадрат) Пирсон критериін

қарастырайық.

(хи квадрат) критерийін пайдалану эмпирикалық үлестірудің теориялық үлестіруге жуықтау дәрежесін бағалауға мүмкіндік береді. Сөйтіп тәжірибелік үлестірудің нормаль үлестіру болуы туралы болжамды не қабылдау, не қабылдамауға мүмкіндік береді. Пирсон критерийін пайдалану

мына ережемен орындалады:

1) Таңдамалы орта және σТ табу керек.

2) Теоретикалық жиіліктерді есептеу: =

Мұндағы, n – таңдама көлемі;

h – қадам (көрші варианталардың айырымы h)

Ui = - шарттық варианта ;

= ; ; - шарттық сәттер;

- Лаплас функциясы (мәндері 1-ші қосымшадан алынады)

3) бақылау мәндерін мына формула арқылы есептеуге болады:

4) Еркіндік дәреже санын есептеу К= S-3;

S – таңдаманың бөлінген топтар саны

5) Мәнділік деңгейі α-ны таңдау

6) Х2 үлестірімнің кризистік нүктелер кестесінен мәнін табамыз

(6-шы қосымшадан)

7) Егер > болса, онда мәні критеришілік облыста болып

Но болжамы қабылданады, яғни тәжірибелік үлестіру мен теориялық үлестіру

айырмасы маңызды емес, демек Пирсон критерийінің мәні қабылдау

облысында жатыр дейміз.

8) Егер < болса, онда мәні критери ішілік облыста болып

Но болжамы қабылданбайды, яғни тәжірибелік үлестіру мен теориялық

үлестіру айырмасы маңызды делінеді.

(хи - квадрат) үлестіруі. - тәуелсіз қалыпты үлестірілген кездейсоқ шамалар. және сәйкесінше математикалық үміттер, орташа квадраттық ауытқулар, яғни Онда , тәуелсіз қалыпты үлестірілген стандартты кездейсоқ шамалар болады, . Кездейсоқ шама , n еркіндік дәрежелі хи – квадрат үлестіруі болады, егер

Еркіндік дәрежесін деп белгілейміз, қосындылар құрамына кіретін кездейсоқ шамалар саны, ал кездейсоқ шамаларды байланыстыратын сызықтық теңдеулер саны. ( хи – квадрат) кездейсоқ шаманың еркіндік дәрежесі санымен анықталады. Олай болса, Хи – квадрат үлестіруінің математикалық үміті және дисперсиясы:

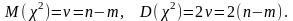
Егер 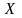және тәуелсіз үлестірілген еркіндік дәрежелері және кездейсоқ шамалар болса , онда олардың қосындысы да еркіндік дәрежесі -ға тең үлестірілген кездейсоқ шама болады. үлестіруі статистикалық болжамдарды тексеруде интервалдық бағаларды табу үшін қолданылады.