1.Статистика туралы ұғым оның маңызы мен қолдану аймақтарын түсінік. Статистика кең мағынада, табиғат пен қоғамның көптеген құбылыстарының сапалық ерекшеліктерін айқындау үшін сол құбылыстарға жүргізілетін сандық талдау туралы ғылым. Статистика жекеленген бірліктерді емес, сол жеке бірліктердің жиыны болып табылатын жиынтықтарды зерттеу үшін пайданылады. Статистика әдістерін дұрыс қолдану үшін басты шарт ол зерттелетін материалдың сапалық біркелкілігі болып табылады. 1889 жылы ағылшын ғалымы Ф. Гальтон математикалық статистика әдістерін бірінші рет биологиялық құблыстарды- өзгергіштік және тұқым қуалаушылықты зерттеу үшін пайдаланды. Ф. Гальтон тірі табиғатты зерттеу үшін статистикалық әдістерді пайдалану жолдарын үйрететін жаңа ғылым- биометрияның

( биос- тіршілік, метрейн- өлшеу) негізін салушы юолып табылады.

2.Биологиядағы математика статистикалық тәсілдердің рөлін және жиынтықтың статистикалық сипаттаңыз. Тірі организмдердің даму процестері өте күрделі, оларды қоршаған орта жағдайлары мен олардың тұқым қуалаушылық қасиеттері әртүрлі болғандықтан, ең алдымен сол обьектілердің өзіне биологиялық зерттеу жүргізу керек. Тек сонан соң ғана оларды сапа жағынан біркелкі топтарға бөліп, математикалық талдауға салу керек. Вариациялық статистика терминін ғылымға 1899 ж Дункер кіргізді. Ол термин биологиялық құблыстарды математикалық статистика әдістері арқылы зерттеу керектігін білдірді. ХХ ғасырдың 30- шы жылдарында математикалық статистика әдістері еліміздің әртүрлі тәжірбие жұмыстарында және биологияда кең түрде қолданыла бастады. Отанымыздың белгілі ғалымдары Ю. А. Филипченко, А.А. Сапегин, П. Н. Константинов, Н. Ф. Деревицкий тб вариациялық статистиканы кең түрде түсіндіріп таратумен қатар оның дамуына өздерінің үлкен үлесін қосты.

3.Қателіктердің протуберанциясы деген ұғымға түсініктеме беріңіз, гистограммалардың құрылуы және оны сипаттаңыз.

Практикалық жұмыстарда кейде жекеленген варианттардың жиілігі кенет көтеріліп немесе төмендеп кететін жағдайлары байқалады. Қисықтың осындай шығыңқы жері қателіктер протуберанцасы деп аталады. Олардың пайда болу себептері; Зерттелуші обьектілер санының жетіспеуі ; Зерттелуші белгілердің тым ұсақ градациялануы; Санағанда немесе өлшегенде жіберілген қателіктер. Дәндер санының әрқайсысын жеке варианта етіп алсақ, онда қателіктер протуберанцасын аламыз. Осы дәндердің әрқайсысын жеке варианта жасамай әрбір екі дәнді бір класқабіріктірсек, онда біздің қисығымыз бірқалыпты дұрыс болып шығады. Ал екі көрші жатқан дәндер санын біріктіріп класс жасау гистограмма алуға мүмкіндік берді. Кластардың ортасын түзу сызықпен қосу арқылы осы гистограммадан дәндер саны бірқалыпты тарап бөлінетін қалыпты вариациялық қисық алуға болады. Кластарға жіктелген вариациялық қатарды график арқылы бейнелеу гистограмма деп аталады. Гистограмма жасаган кезде горизонталь осьтіңтбойына жиіліктерді орналастырады. Гистограмманы вариациялық қисыққа айналдыруға болады. Ол үшін кластардың ортасын түзу сызықтармен қосу керек. Талдау кезінде әдетте зерттеуші көп санды мәліметтер алады. Гистограммалар мен вариациялық қисықтар құру сол алынған көп санды мәліметтердің мәнін түсінуге және олардан қандай да болмасын белгілі заңдылық табуға көмектеседі.

4.Арифметикалық орта шама және оның қасиеті Түзетпе, орташа шама, ауытқу түсініктеріне анықтама беріңіз.

Биологиялық және ауылшаруашылық ғылыми-зерттеу жұмыстарында көбнесе арифметикалық орта шаманы табудың үлкен маңызы бар. Өзінен оң және теріс ауытқуларының қосындысы нөлге тең шама- арифметикалықторта шама деп аталады. . Арифметикалық орта шаманы табу үшін барлық варианттарды қосады және оларды бақылаулар санына бөледі. Вариациялық статистикада арифметикалық орта шама М немесе х^- ( икс покрытое деп оқылады.) арқылы белгіленеді және төмендегі екі формуламен кез келгені бойынша белгіленеді. Мысалы 3 өсімдіктің жемістерінің саны 4,5,6 болсын делік. Осы 3 өсімдіктердің жемістерінің орта шамасы (4+5+6):3=6 болады. Осы орта шамадан 4=(-2) ,5=(-1) ,9=3 болып ауытқиды. Яғни оң және теріс ауытқулардың қосындысы (-2)+ (-1)+3 = 0. Арифметикалық орта шаманы табу үшін мына формуланы қолданамыз.

х немесе M=∑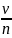

Алынған кездейсоқ орта шамадан ауытқулар а немесе х-х^- (икс покрытое) арқылы белғіленеді. Кездесоқ алынған орта шама (немесе шартты орта шама) ретінде вариациялық қатардың дәл ортасында немесе ортасында жақын жатқан кез келген вариантаны аламыз және оны қос түзу сызықпен белгілеп шектейміз. Біз келтірілген осы мысалмызда кездейсоқ орта шама 13 вариантын алдық. Енді әрбір вариантынтың осы өзіміз алған кездейсоқ шартты орта шамадан ауытқуларын есептейміз. Біз орта шамадан оң және теріс ауытқулардың қосындысы нөлге тең болатынын білеміз. Сондықтан алынған ауытқулардың қосындысын бақылаулар санына бөліп түзетуді табамыз. Түзетудің формуласы в=∑

Кластарға жіктелген вариациялық қатарлардан орта шама тапқан кезде әр кластың кездесоқ алынған шартты орта кластан ауытқу бірге тең деп есептелінеді. Сонан соң табылған түзетуді k немесе i әріптерімен белғіленетін класс мөлшеріне көбейтеді де таңбасына қарай кездесоқ шартты орта кластың шамасына не қосады не одан алып тастайды. Кездесоқ кластың орталық мәні W немесе х арқылы белгіленеді.

5. Қандай жағдайда арифметикалық орта шаманы есептеуде маманттер тәсәлін қолдану керектігін түсіндіріңіз. Арифметикалық орта шаманы х есептеп шығаруға тек бақылаулар саны аз болғанда қолданылады. Арифметикалық орта шаманы осылайша есептеу тек бақылаулар саны аз болғанда ғана немесе электрондық есептеу машиналарын пайдаланған кезде ғана қолданылады. Варианттардың саны көп күрделі вариациялық қатарларды өңдеген кезде арифметикалық орта шаманы осылайша есептеу көп еңбек сіңіруді қажет етеді. Сондықтан орта шаманы есептеу үшін моменттер әдісі немесе кез келген бастама әдісі қолданылады.