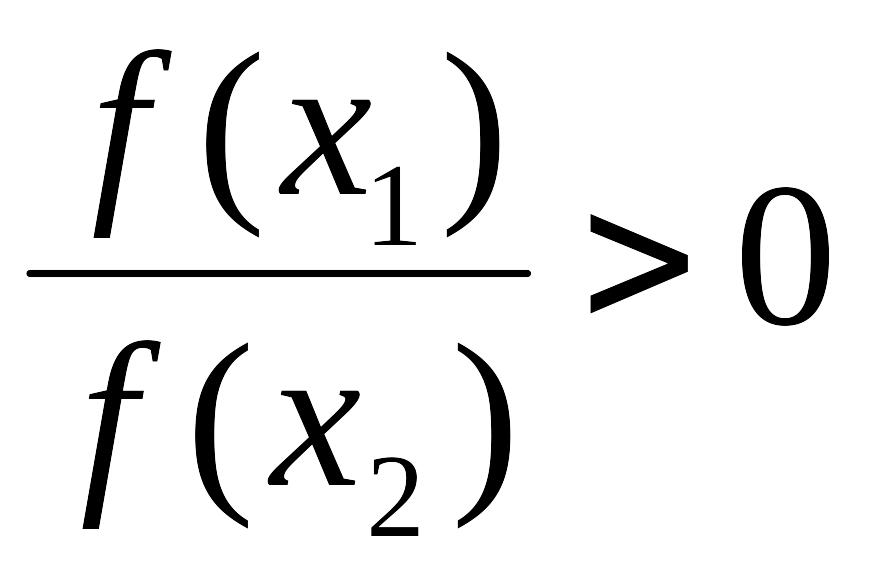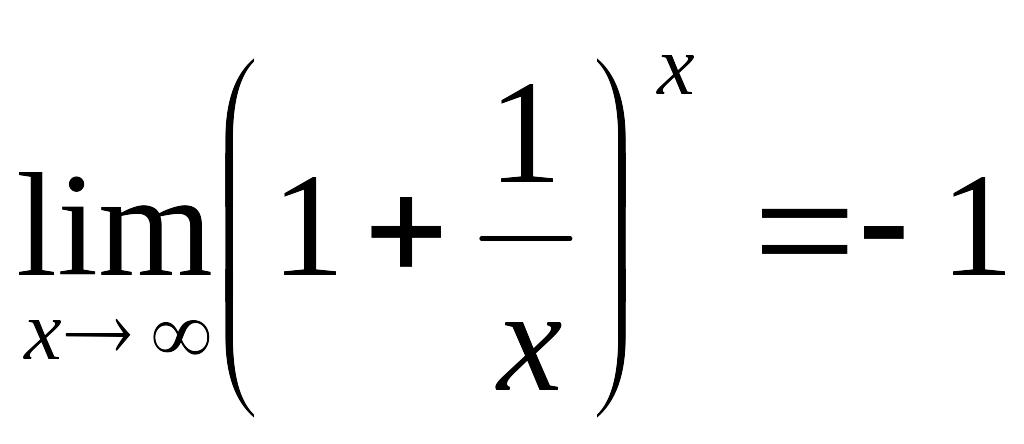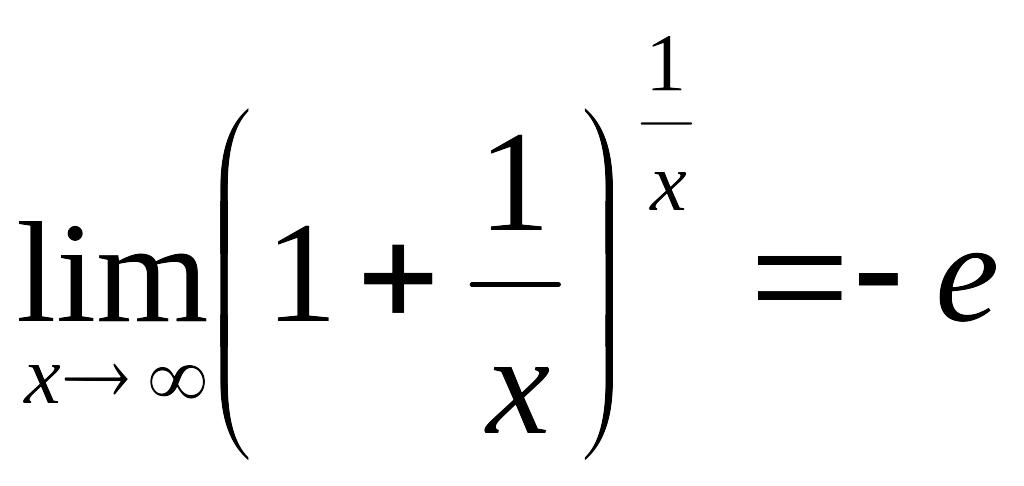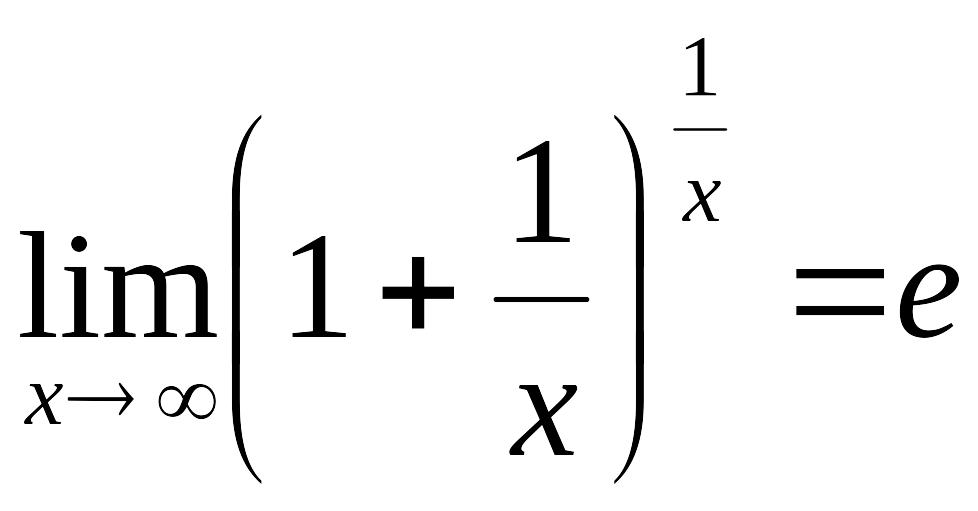1 Раздел
1. Бесконечно малые
функции
![]() и
и
![]() при
при
![]() называются эквивалентными, если:
называются эквивалентными, если:
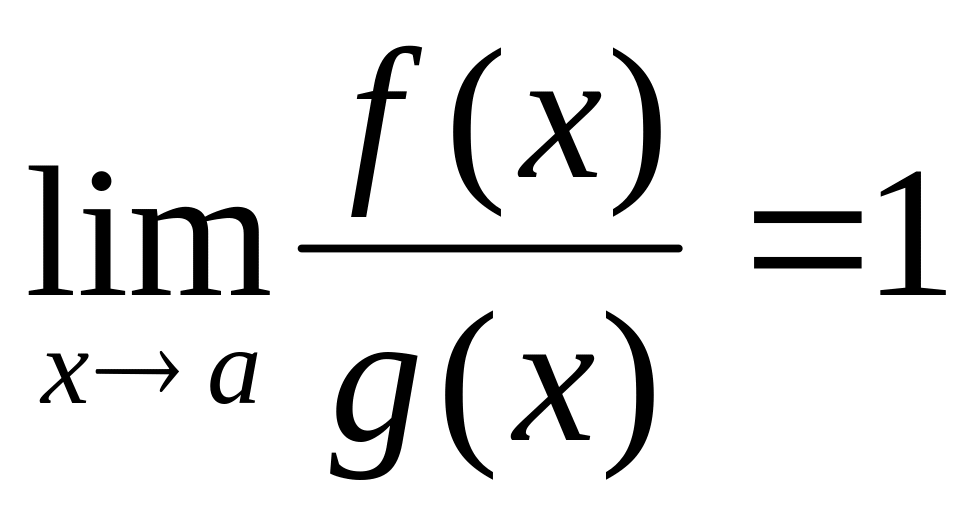 !!!!!
!!!!!
2. Число
![]() называется пределом последовательности
называется пределом последовательности
![]() ,
если для любого
,
если для любого
![]() найдется такой номер
найдется такой номер
![]() ,
что для:
,
что для:
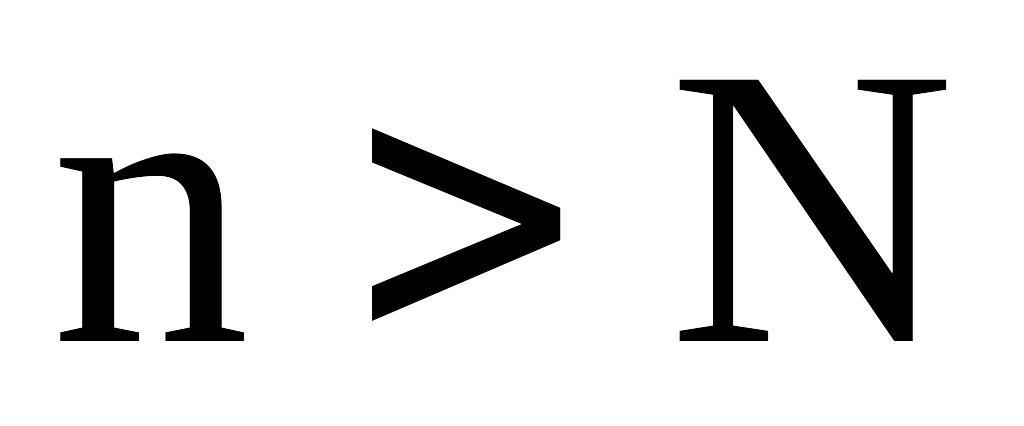 выполняется
выполняется
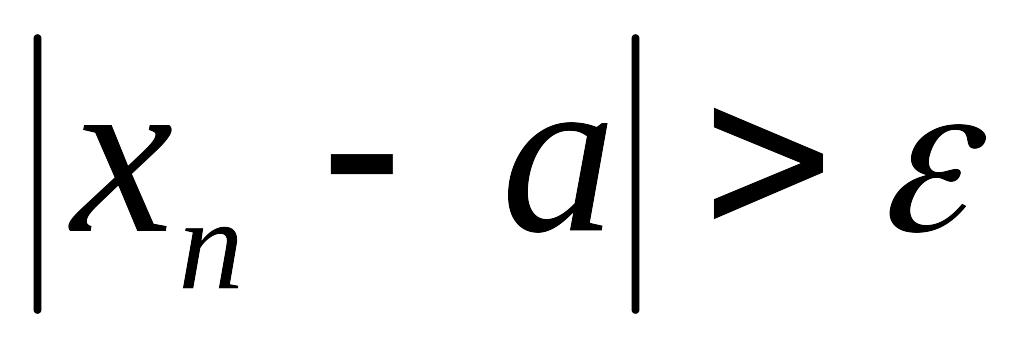
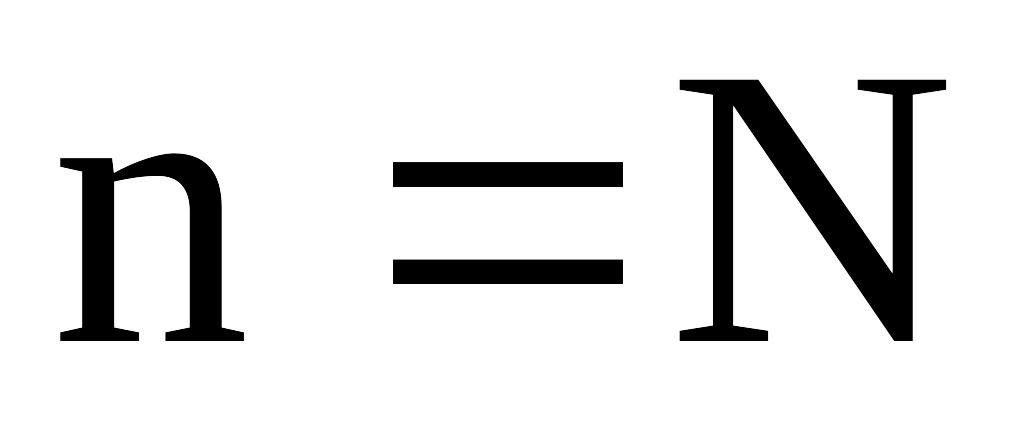 выполняется
выполняется
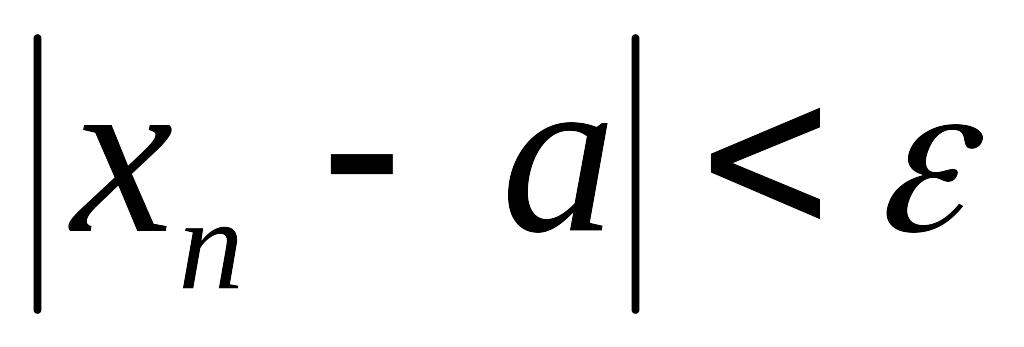
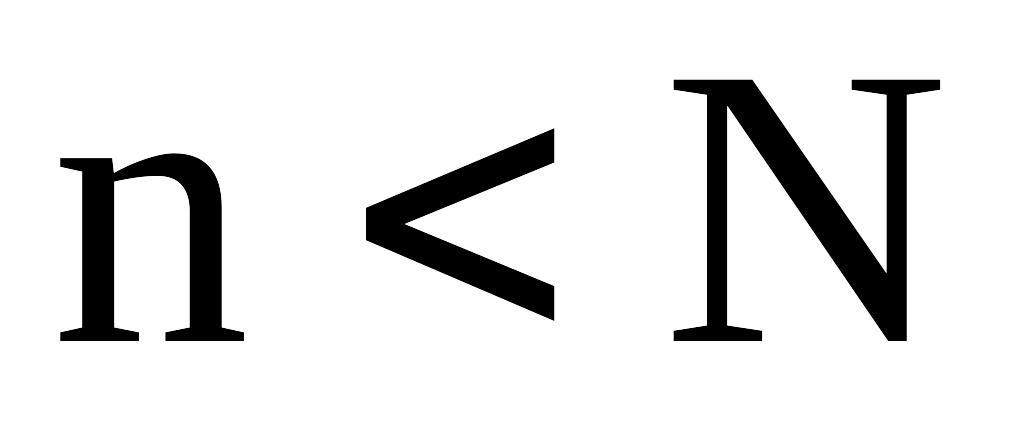 выполняется
выполняется
выполняется !!!!!!!!!!!
выполняется

3. Из сходимости последовательности следует, что она:
Ограничена!!!!!!!!!
не ограничена
убывающая
монотонна
возрастающая
4. Если последовательность
![]() -
ограничена, а
-
ограничена, а
![]() -
бесконечно большая последовательность,
то:
-
бесконечно большая последовательность,
то:
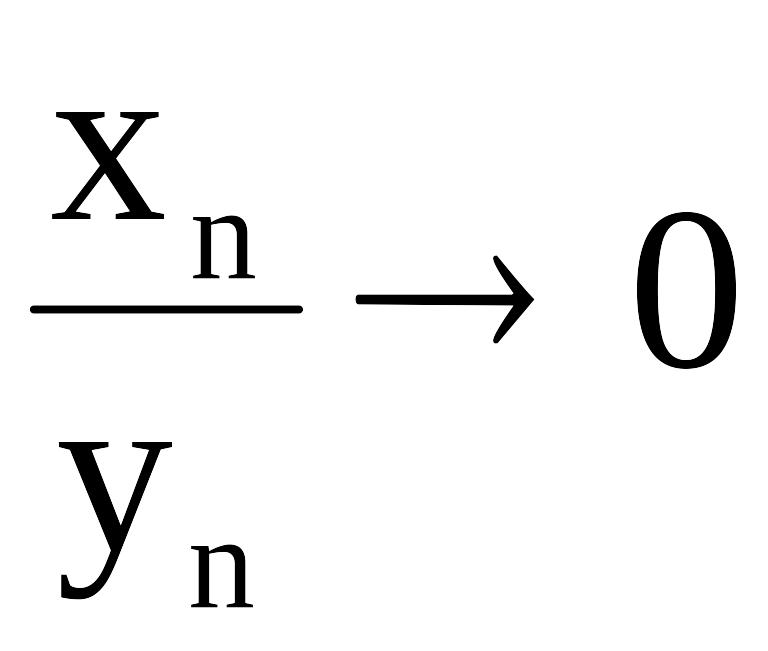 при
при
 !!!!
!!!!
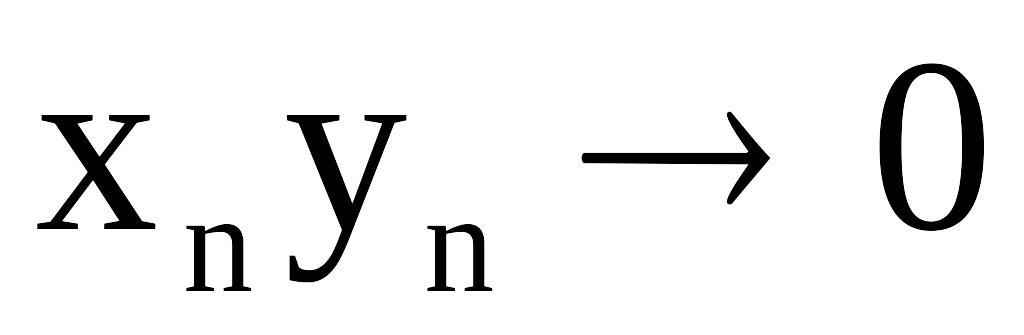 при
при
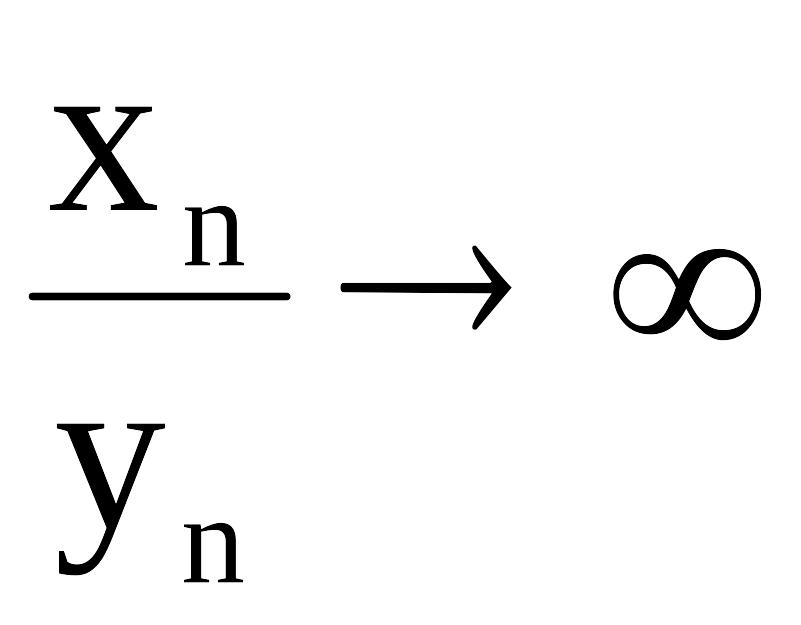 при
при
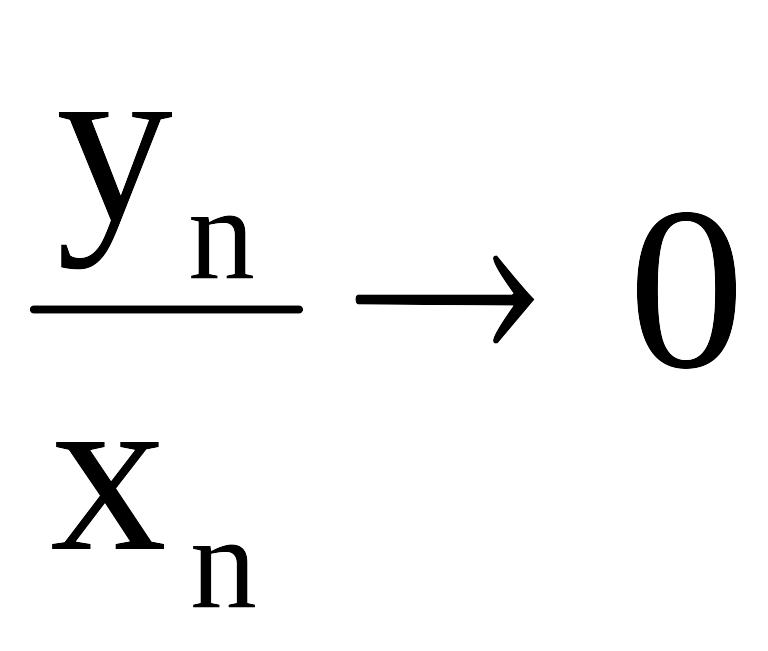 при
при
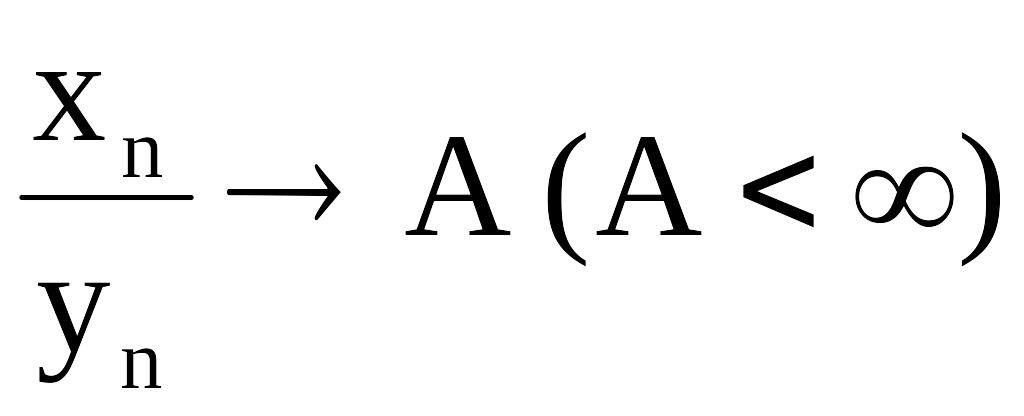 при
при
5. Для того, чтобы
существовал предел
![]() ,
необходимо и достаточно, чтобы:
,
необходимо и достаточно, чтобы:
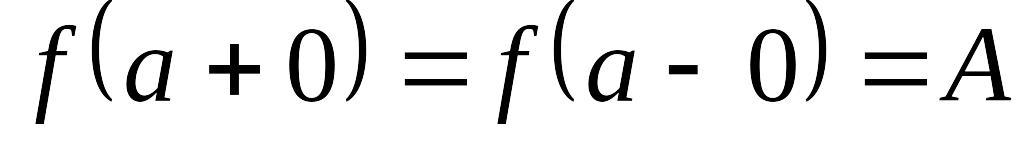 !!!!
!!!!
6. Функция
![]() в точке
в точке
![]() непрерывна, если
определена в точке
непрерывна, если
определена в точке
![]()
![]() и в некоторой её окрестности, и выполняется
равенство:
и в некоторой её окрестности, и выполняется
равенство:
 !!!!!!!!!
!!!!!!!!!
7.
Если функция
непрерывна на
![]() ,
то она на
:
,
то она на
:
Ограничена
ограничена или не ограничена
Не ограничена
имеет период
нечетна
8. Функция
![]() называется возрастающей в некотором
интервале, если для любых
называется возрастающей в некотором
интервале, если для любых
![]() таких, что
таких, что
![]() ,
выполняется неравенство:
,
выполняется неравенство:
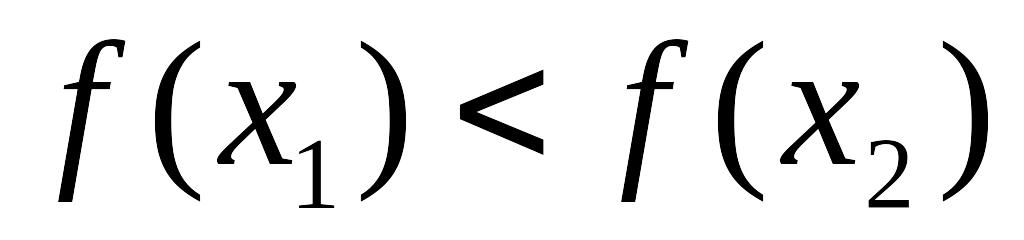 !!!!!!!!!!!
!!!!!!!!!!!
9. Указать первый замечательный предел:
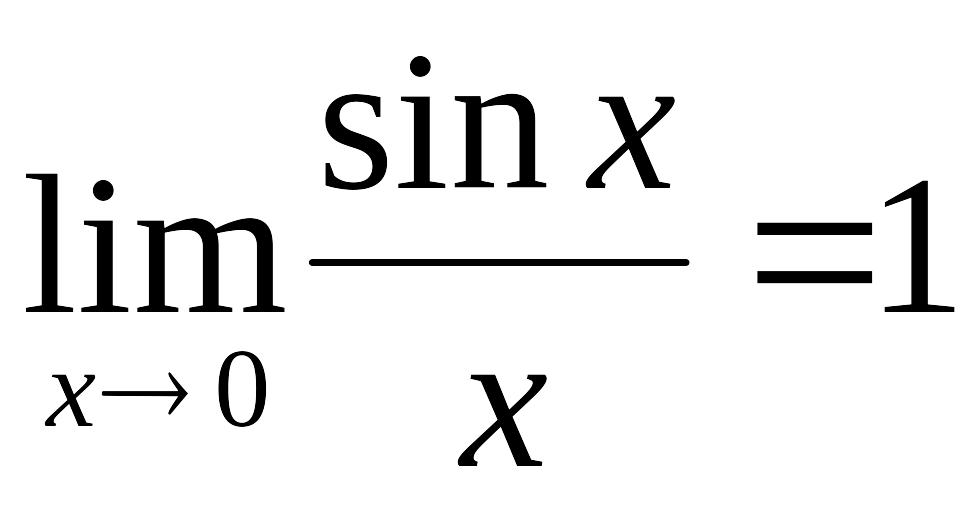 !!!!
!!!!
10. Указать второй замечательный предел:
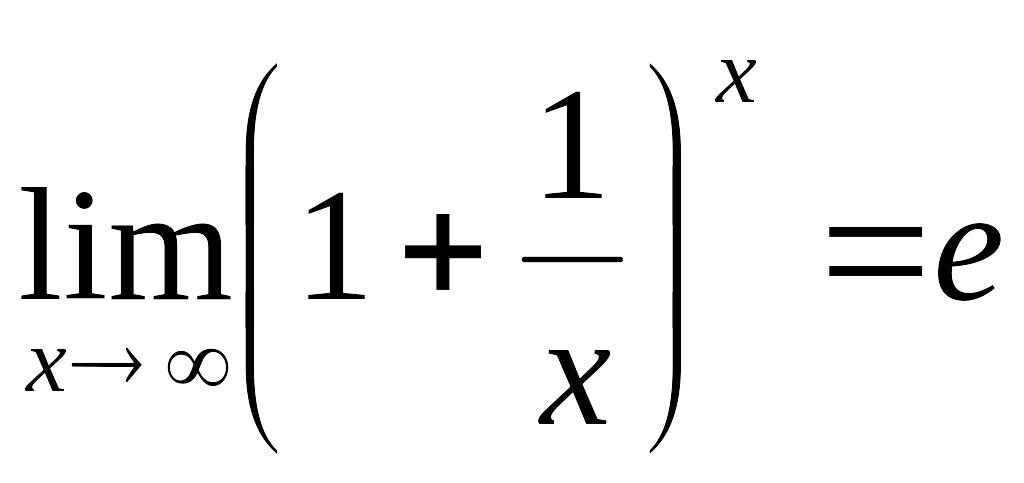 !!!!!!!!!!!!!
!!!!!!!!!!!!!
11.
Если в какой-либо точке
![]() функция
функция
![]() не является непрерывной, то точка
называется:
не является непрерывной, то точка
называется:
областью определения
точкой экстремума
точкой минимума
точкой максимума
точкой разрыва функции
12. Если производная дифференцируемой функции положительна внутри некоторого промежутка, то:
функция не постоянна
функция убывает на этом промежутке
функция постоянна на этом промежутке
функция возрастает на этом промежутке
функция положительна на этом промежутке
13. Если производная
![]() от функции
от функции
![]() всюду в интервале отрицательна, то
функция
в этом интервале:
всюду в интервале отрицательна, то
функция
в этом интервале:
равна нулю
возрастает
постоянна
убывает
имеет экстремум
14.
Функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
![]() .
Если для любого
.
Если для любого
![]() существует
существует
![]() такое, что для любого
такое, что для любого
![]() из
из
![]() выполняется неравенство
выполняется неравенство
![]() ,
то:
,
то:
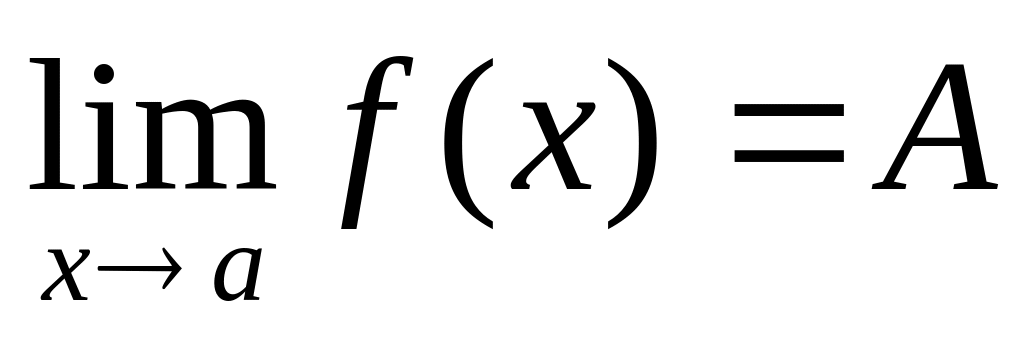 !!!!!!!!!!!!
!!!!!!!!!!!!
15. Если функция
дифференцируема в точке
![]() и имеет в этой точке локальный экстремум,
то:
и имеет в этой точке локальный экстремум,
то:
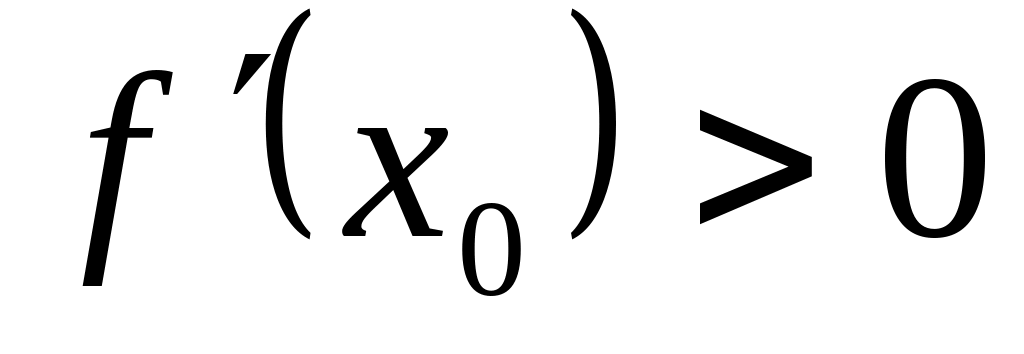 !!!!!!!!!!
!!!!!!!!!!
16.
Производная функции
в точке
обозначается
![]() и определяется как:
и определяется как:
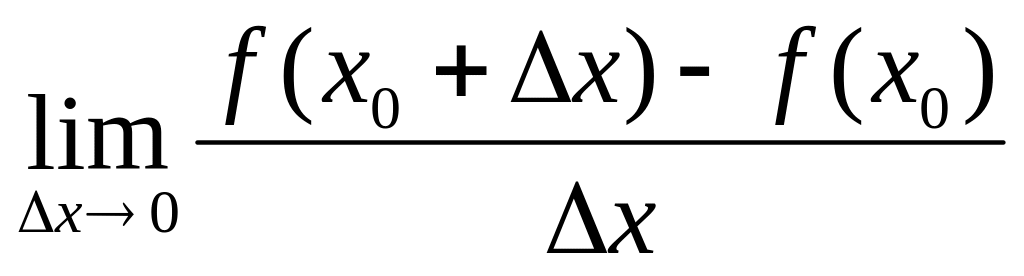 !!!!!!!!!!!!!
!!!!!!!!!!!!!
17. Для того, чтобы
функция
![]() возрастала на интервале
возрастала на интервале
![]() ,
достаточно,
,
достаточно,
чтобы производная
![]() была на этом интервале:
была на этом интервале:
отрицательной
положительной
неположительной
неотрицательной
равной нулю
18. Для того, чтобы
функция
убывала на интервале
![]() ,
достаточно,
,
достаточно,
чтобы производная
![]() была на этом интервале:
была на этом интервале:
неположительной
положительной
неотрицательной
отрицательной
не равной нулю
19. Если функция
имеет наклонную асимптоту
![]() ,
то
,
то
![]() :
:
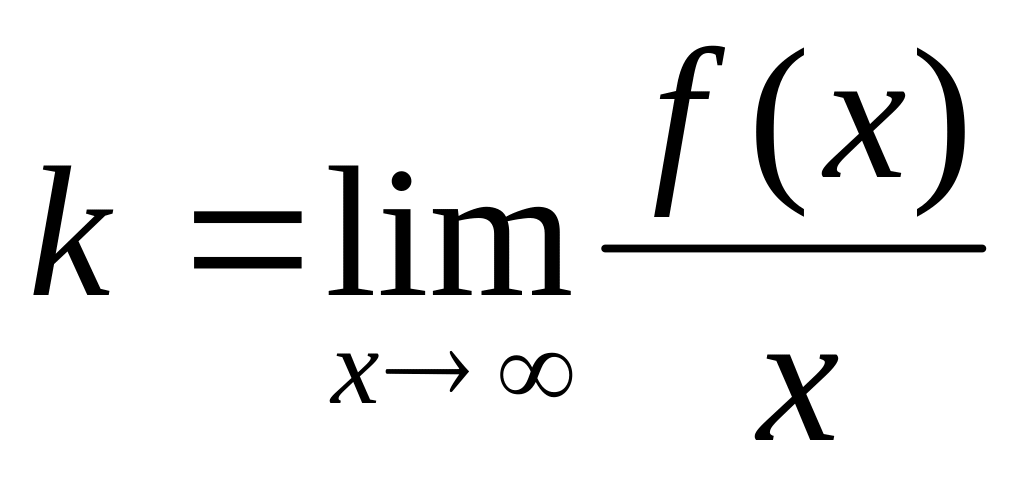 !!!!!!!!!!!!!
!!!!!!!!!!!!!
20.
Уравнение касательной к графику функции
в точке
![]() имеет вид:
имеет вид:
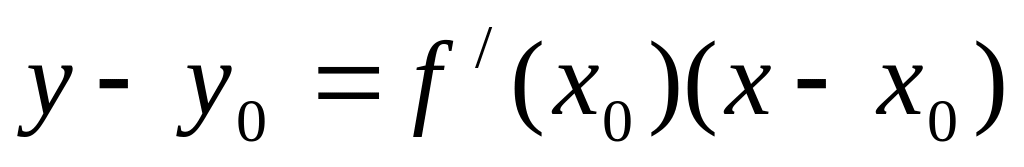 !!!!!!!!!!!!!
!!!!!!!!!!!!!
21. Уравнение нормали к графику функции в точке имеет вид:
!!!!!!!!!
22. Если график функции выпуклый на интервале (a,b) и на этом интервале существует f//(x), то на этом интервале:
f//(x)=0
f//(x)>0
f//(x)<0 !!!!!!!!
f//(x)
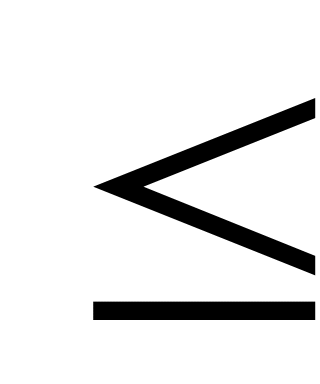 1
1
f//(x)
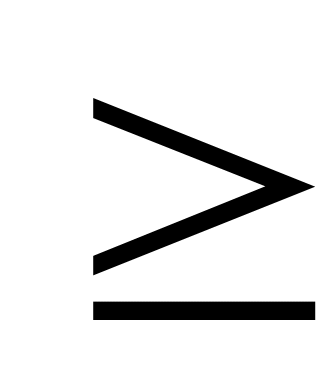 0
0
23.
Если график функции вогнутый на интервале
![]() и на этом интервале существует
и на этом интервале существует
![]() ,
то на этом интервале:
,
то на этом интервале:
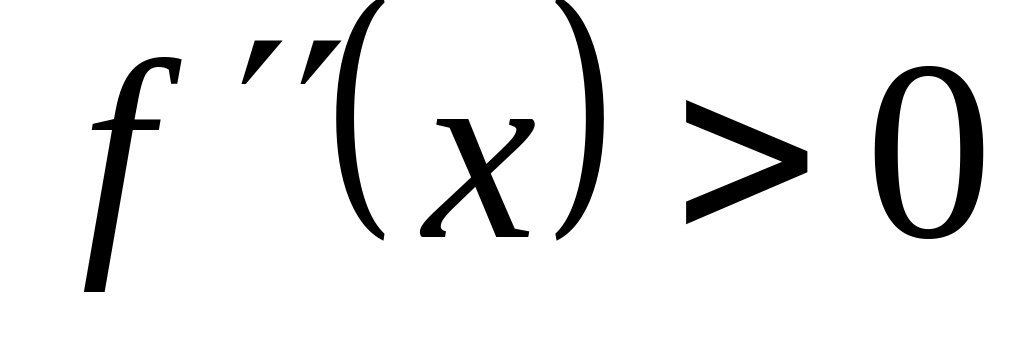 !!!!!!!!!!
!!!!!!!!!!
24. Пусть функция
дважды дифференцируема в точке
![]() и
и
![]() .
.
Тогда функция
имеет в точке
![]() локальный максимум, если:
локальный максимум, если:
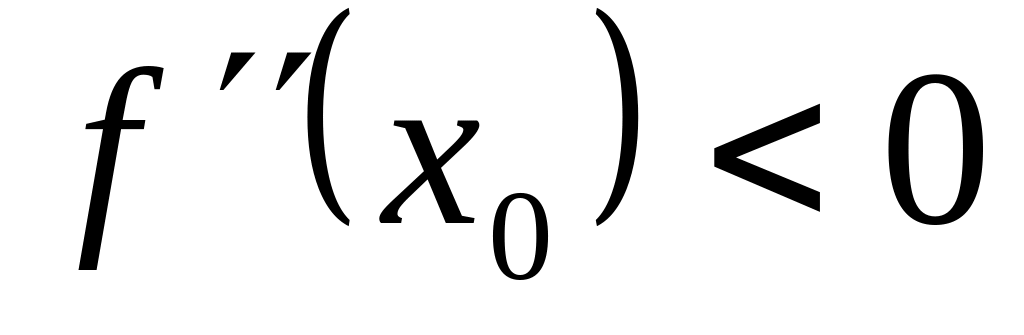 !!!!!!!!
!!!!!!!!
25. Пусть функция дважды дифференцируема в точке и .
Тогда функция имеет в точке локальный минимум, если:
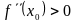 !!!!!!!!!!!
!!!!!!!!!!!