2 Цифровые интегральные схемы

2.1 Основные логические операции и логические элементы.

Логические функции ‑ функции, которые принимают два значения:

F=0, если сообщение ложное,

F=1, если сообщение истинное.

Логические операции описывают связь между логическими функциями.

Электрические схемы, реализующие элементарные логические операции, называются логическими элементами (ЛЭ).

Существуют 3 простейших логических операции: НЕ, ИЛИ, И.

а) Операция НЕ - логическое отрицание, инверсия.

(F равно не А)

ЛЭ, выполняющий операцию НЕ, называется инвертором (рисунок 2.1). Его таблица истинности приведена в таблице 2.1.

Таблица 2.1

А
0	1
1	0

Временные диаграммы приведены на рисунке 2.2.

Здесь потенциал Е принимается за единичное значение “1”. За ноль принимается нулевое значение логической функции.

Простейшая реализация инвертора ‑ транзисторный ключ (рисунок 2.3).

При А = 1, т.е U_ВХ = E, транзистор открыт и насыщен. U_ВЫХ= U_кн = 0, т.е. .

При А = 0, т.е. U_ВХ = 0, транзистор заперт, U_ВЫХ = Е_к, т.е. .

б) Операция ИЛИ ‑ логическое сложение, дизъюнкция.

F=АВ, либо F=А+В (F есть А или В).

ЛЭ, выполняющий операцию ИЛИ, называется сборкой или дизъюнктором (рисунок 2.4). Таблица истинности для операции ИЛИ показана в таблице 2.2.

А	В	А+В
0	0	0
0	1	1
1	0	1
1	1	1

Таблица 2.2

Временные диаграммы приведены на рисунке 2.5. Выходной сигнал равен единице, если хотя бы один из аргументов равен единице.

Простейшая реализация операции ИЛИ возможна на диодной сборке (рисунок 2.6).

В схеме достаточно подать “+Е” хотя бы на один из входов, чтобы на выходе появился положительный сигнал Е, т.е. F = 1.

в) Операция “И”- логическое умножение или конъюнкция.

F=A B (F есть А и В);

F=AB.

Логический элемент, выполняющий операцию И называется схемой совпадения, или конъюнктором (рисунок 2.7).

Таблица 2.3

А	В	АВ
0	0	0
0	1	0
1	0	0
1	1	1

Таблица истинности приведена в таблице 2.3.

На рисунке 2.8 показаны временные диаграммы конъюнктора (рисунок 2.7), из которого видно, что выходной сигнал равен единице, только в том случае, если все входные сигналы равны единице.

Простейшая реализация операции И возможна на диодной схеме совпадения (рисунок 2.9).

В схеме R_H >> R. Если хотя бы на одном из входов низкий уровень напряжения, т.е. около нуля, откроется диод на этом входе, потечет ток через открытый диод, и напряжение на R_H U_ВЫХ будет равно нулю. U_ВЫХ будет равно единице только в случае, если запрутся все диоды на входе, т.е., если на всех входах высокий уровень напряжения.

Этот набор элементов И, НЕ, ИЛИ называется основным базисом или основной функционально полной системой элементов. Т.е. с помощью только этих элементов можно создать любую логическую схему.

Более широко в схемотехнике используются элементы других базисов ‑ двухступенчатые ИЛИ-НЕ, И-НЕ:

а) стрелка Пирса, или отрицание дизъюнкции, или операция ИЛИ-НЕ

АВ = .

Условное обозначение приведено на рисунке 2.10. Логический элемент называется элементом Пирса.

Таблица истинности представлена в таблице 2.4

Таблица 2.4

А	В
0	0	1
0	1	0
1	0	0
1	1	0

б) Штрих Шеффера, или отрицание конъюнкции, или операция И-НЕ

АВ = . Таблица истинности представлена в таблице 2.5.

Таблица 2.5

А	В
0	0	1
0	1	1
1	0	1
1	1	0

У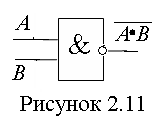 словное обозначение приведено на рисунке 2.11. Логический элемент называется элементом Шеффера.

С помощью только одного типа микросхем ИЛИ-НЕ, либо И-НЕ можно построить любую логическую схему, т.е. каждая из них является основным базисом.

Самым распространенным является элемент Шеффера И-НЕ.

Т акже широкое применение нашли многоступенчатые логические элементы:

а) 2И-ИЛИ-НЕ, выполняющее операцию . Условное обозначение приведено на рисунке 2.12.

б) исключающее ИЛИ, или сумма по модулю два, или функция неравнозначности имеет вид

F = Это означает, что F равно либо A, либо B. Логический элемент исключающее ИЛИ иногда называют элементом типа «что-нибудь, но не все». Символ (псевдоплюс) означает, что входы А и В связаны логической функцией исключающее ИЛИ.

Из алгебры логики известно:

; ; .

Таблица истинности для элемента исключающее ИЛИ приведена в таблице 2.6.

Таблица 2.6

А	В	А В
0	0	0
0	1	1
1	0	1
1	1	0

Из таблицы видно, что, если на какой-либо из входов (но не на все) подана логическая единица, то на выходе также появляется единица. Сравните с таблицей 2.3 (ИЛИ).

Условное обозначение элемента неравнозначности приведено на рисунке 2.13,а. Поскольку этот элемент выполняет операцию сложения по модулю 2, то его обозначают так же, как на рисунке 2.13,б.

в) исключающее ИЛИ-НЕ, или функция равнозначности имеет вид

. Это означает, что F равно инверсии либо A, либо B.

Таблица истинности для элемента исключающее ИЛИ-НЕ приведена в таблице 2.7.

А	В
0	0	0
0	1	1
1	0	1
1	1	0

Таблица 2.7

Условное обозначение элемента равнозначности приведено на рисунке 2.14