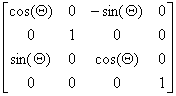Робертс алгоритмі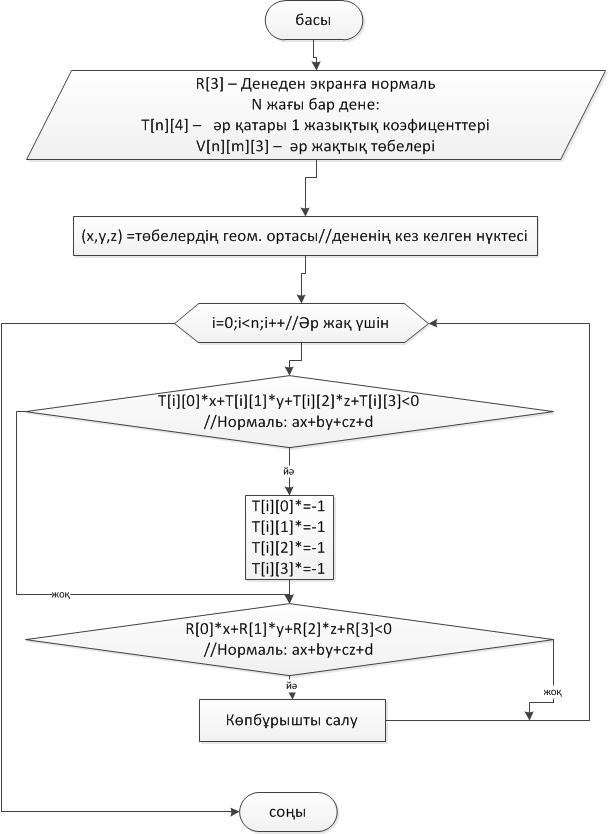

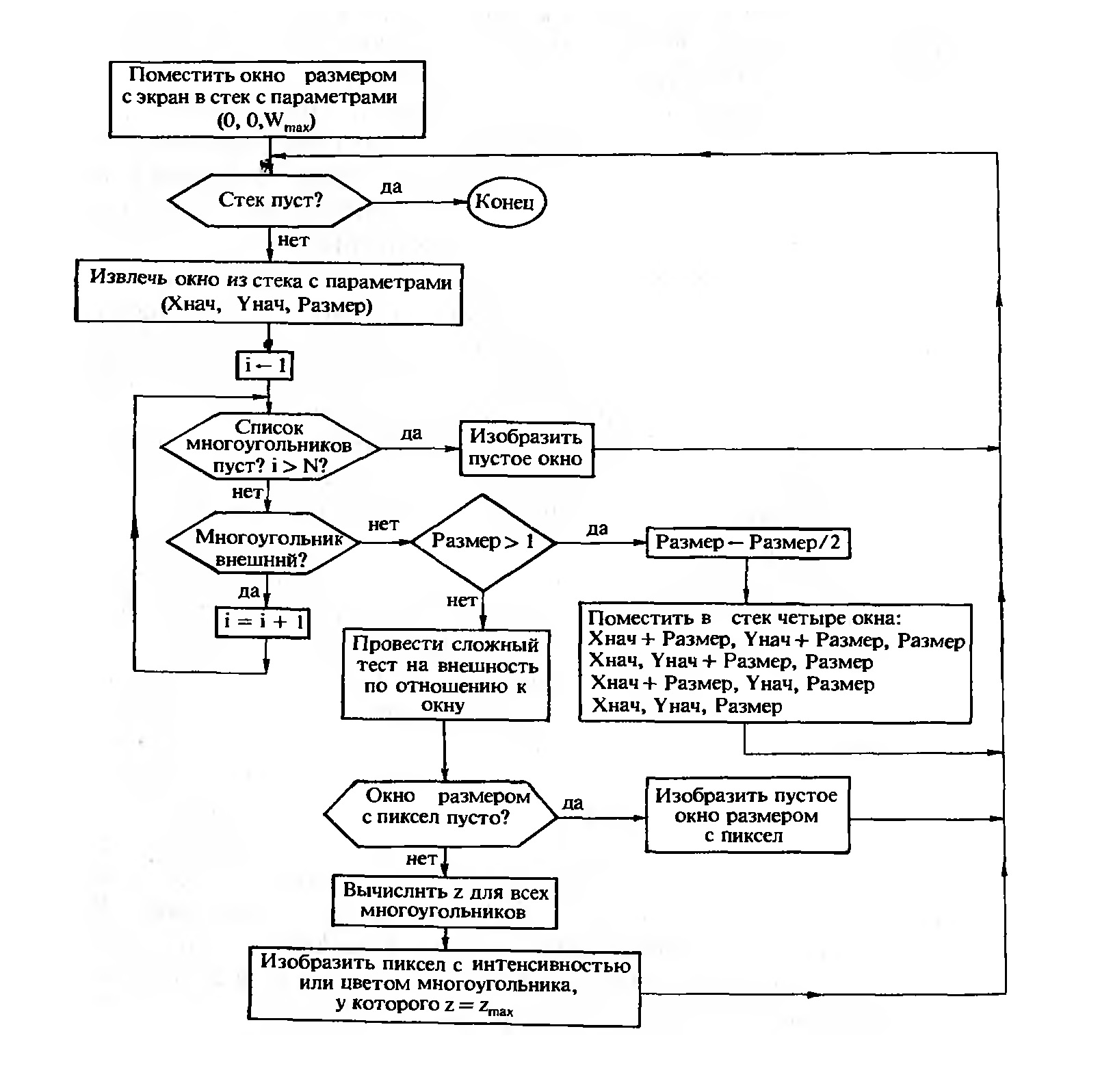
Варнок алгоритмі

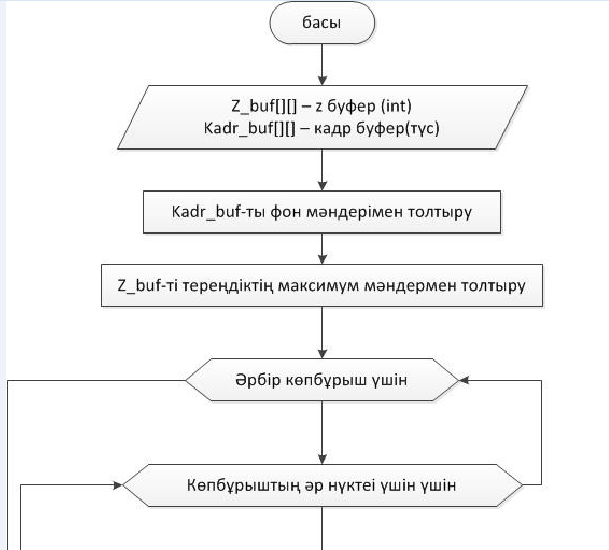
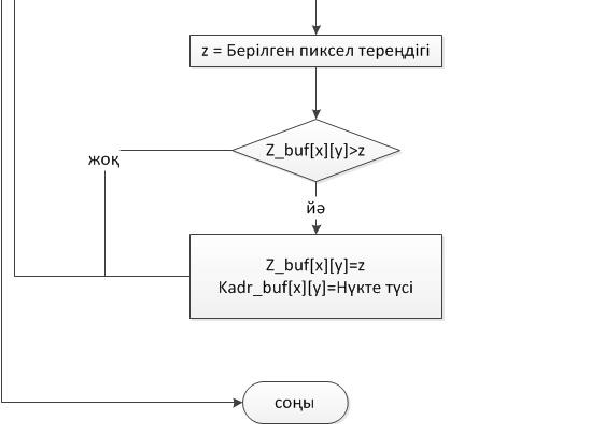
Z-буферә

1. Мониторлар, мониторлардың сипаттамалары

2. Дербес компьютердің видеожүйесі

3. Компьютерлік графиканың түрі. Растрлі графика. Мысал келтіріңіз.

4. Растрлі графиканың артықшылықтары мен кемшіліктері. Мысал

5. Векторлы графиканың матем негіздері. Артықш мен кемш. Мысал

6. Когнитивті графика. Мысал келтіріңіз.

7. Фракталды графика. Мысал келтіріңіз.

8. Екі өлшемді түрлендірулер.

9. Бір тектес координаталардағы екі өлшемді түрлендіру.

10.Үш өлшемді координаталар.

11. Бейнелерді растрлі жəне векторлы бейнелеу.

12. Бейнелеудің ерекшеліктері мен кемшіліктері.

13. Шекаралық-байланыстық аймақты бояу.

14. Көпбұрышты толтыру: облыстарды растрде толтыру.

15. Көпбұрышты толтыру: жол бойынша толтыру.

16. Нүкте мен полигонның жазықтықта өзара орналасуын шешудің əдістері.

17. Біртекті координаталарды елестету. Нормалау операциялары.

18. Екіөлшемді түрлендірудің толық матрицасы.

19. Шеңберді растрге келтіру.

20. Аффинді түрлендіру.

21. Үшөлшемді түрлендірудің толық матрицасы.

22. Біртекті координаталар жəне негізгі геометриялық түрлендірулер.

23. RGB, CMY, CMYK – координаталардың түс жүйелері.

24. Екіөлшемді түрлендіру. Координата басына қарағанда бұрылу, қозғалу.

25. Екіөлшемді түрлендіру. Координата басына қарағанда масштабталу, шағылысу операциялары.

26.Жобалап түрлендіру.

27. Жазықтықта полигондардың өзара орналасу мəселелері. Алгоритмдері.

1. Векторлар генерациясы үшін Брезенхем алгоритмі. Блок-схемасын сыз

2. Шеңбердің генерациясы үшін Брезенхем алгоритмі. Блок-схемасын сыз

3. Аймақты белгімен бояу: бояудың қарапайым алгоритмі. Блок-схемасын

4. Көрінбейтін бөліктердің жою тəсілі. Мысал келтіріңіз

5. Сызықтарды жою алгоритмі№ Блок-схемасын сызыңыз

6. Z-буферімен үстіңгі бетті жою алгоритмі. Блок-схемасын сызыңыз

7. Варнок алгоритмі. Блок-схемасын сызыңыз

8. Робертс алгоритмі. Блок-схемасын сызыңыз

9. Векторлар генерациясы үшін Брезенхем алгор программасын құрыңыз

10. Шеңбердің генерациясы үшін Брезенхем алгор программасын құрыңыз

11-12. Координата басына қарағанда қозғалуды жүзеге асыратын программаны құрыңыз.

13. Координата басына қарағанда масштабталуды жүзеге асыратын программаны құрыңыз.

3.2.      Трехмерные преобразования и проекции

 

Рассмотрим трехмерную декартовую систему координат, являющуюся правосторонней. Примем соглашение, в соответствии с которым будем считать положительными такие повороты, при которых (если смотреть с конца полуоси  в направлении начала координат) поворот на 90 против часовой стрелки будет переводить одну полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат:

 

 

Если ось вращения	Положительным будет направление поворота
X	От  y  к  z
Y	От  z  к  x
Z	От  x  к  y

 

 

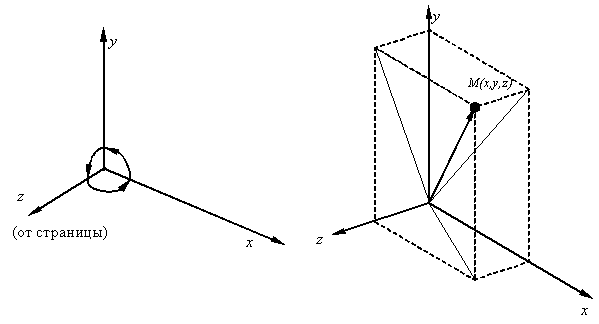
Рис. 3.6. Трехмерная система координат

 

Аналогично тому, как точка на плоскости описывается вектором (x,y), точка в трехмерном пространстве описывается вектором (x,y,z).

Как и в двухмерном случае, для возможности реализаций трехмерных преобразований  с помощью матриц перейдем к однородным координатам:

 

 

[x,y,x,1] или [X,Y,Z,H]

 

[x*,y*,z*1] = [ ], где Н1, Н 0.

 

Обобщенная матрица преобразования 44 для трехмерных однородных координат имеет вид

 

Т =

Эта матрица может быть представлена в виде четырех отдельных частей:

 

.

 

     Матрица 33 осуществляет линейное^[1] преобразование в виде изменения масштаба, сдвига и вращения.

     Матрица 13 производит перенос.

     Матрица 31- преобразования в перспективе.

     Скалярный элемент 11 выполняет общее изменение масштаба.

Рассмотрим воздействие матрицы 44 на однородный вектор [x,y,z,1]:

 

1. Трехмерный перенос – является простым расширением двумерного:

 

T(Dx,Dy,Dz)=

 

т. е. [x,y,z,1]*T(Dx,Dy,Dz)=[x+Dx,y+Dy,z+Dz,1].

 

2. Трехмерное изменение масштаба.

Рассмотрим частичное изменение масштаба. Оно реализуется следующим образом:

 

S(Sx,Sy,Sz)=

 

т. е. [x,y,z,1]*S(Sx,Sy,Sz)=[Sx*x,Sy*y,Sz*z,1].

 

Общее изменение масштаба получается за счет 4-го диагонального элемента, т. е.

 

[x y z 1] *

= [x y z S] = [x* y* z*  1] = [ ].

 

Такой же результат можно получить при равных коэффициентах частичных изменений масштабов. В этом случае матрица преобразования такова:

 

S=

 

3. Трехмерный сдвиг

Недиагональные элементы матрицы 33 осуществляют сдвиг в трех измерениях, т. е.

 

[x y z 1] *

=[x+yd+hz, bx+y+iz, cx+fy+z, 1].

 

4. Трехмерное вращение

Двухмерный поворот, рассмотренный ранее, является  в то же время трехмерным поворотом вокруг оси Z . В трехмерном пространстве поворот вокруг осиZ описывается матрицей

 

Rz( )=

 

Матрица поворота вокруг оси X имеет вид

 

Rx( )=

 

Матрица поворота вокруг оси Y имеет вид

   

Ry( )=

 

Результатом произвольной последовательности поворотов вокруг осей x, y, z  является матрица

 

A=

 

Подматрицу 33 называют ортогональной, так как ее столбцы являются взаимно ортогональными единичными векторами.

Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и сдвига нет.

В вычислительной геометрии известна задача об определении принадлежности точки многоугольнику. На плоскости даны многоугольник и точка. Требуется решить вопрос о принадлежности точки многоугольнику.

Многоугольник может быть как выпуклым, так и невыпуклым. Обычно предполагается, что многоугольник простой, т.е. без самопересечений, но задачу рассматривают и для не-простых многоугольников. В последнем случае разные способы определения принадлежности точки многоугольнику могут привести к разным результатам. Различают алгоритмы без предварительной обработки и алгоритмы с предварительной обработкой, в ходе которой создаются некоторые структуры данных, позволяющие в дальнейшем быстрее отвечать на множество запросов о принадлежности точек одному и тому же многоугольнику.

Содержание

  [убрать] 

• 1 Метод трассировки луча

  • 1.1 Учёт числа пересечений

  • 1.2 Учёт числа оборотов

• 2 Метод суммирования углов

• 3 Алгоритмы c предобработкой

  • 3.1 Выпуклые и звёздные многоугольники

  • 3.2 Произвольный многоугольник

• 4 Примечания

• 5 Литература

• 6 Ссылки

Метод трассировки луча[править | править исходный текст] Учёт числа пересечений[править | править исходный текст]

Методы работают по-разному для многоугольников с самопересекающейся границей. Слева: even-odd rule. Справа: nonzero winding rule.

Один из стандартных методов определения принадлежности точки произвольному простому многоугольнику заключается в следующем. Выпустим луч из данной точки в произвольном направлении (например в положительном направлении горизонтальной оси), и посчитаем сколько раз луч пересекает рёбра многоугольника. Для этого достаточно пройтись в цикле по рёбрам многоугольника и определить, пересекает ли луч каждое ребро. Если число пересечений нечётно, то объявляется, что точка лежит внутри многоугольника, если чётно — то снаружи. Это основано на том простом наблюдении, что при движении по лучу с каждым пересечением границы точка попеременно оказывается то внутри, то снаружи многоугольника. Алгоритм известен под такими названиями, какcrossing number (count) algorithm или even-odd rule.

В алгоритме возникает затруднение в вырожденном случае, когда луч пересекает вершину многоугольника. Один из приёмов для его преодоления заключается в том, чтобы считать, что такие вершины многоугольника лежат на бесконечно малую величину выше (или ниже) прямой луча, и стало быть пересечения на самом деле и нет.^[1] Таким образом, пересечение луча с ребром засчитывается, если один из концов ребра лежит строго ниже луча, а другой конец — выше или лежит на луче.

Алгоритм работает за время O(N) для N-угольника.