§ 18. Длина, площадь, масса, время

101. Длина отрезка и ее измерение

Определение. Длиной отрезка называется положительная величина, определенная для каждого отрезка так, что:

1. равные отрезки имеют равные длины;

2. если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков.

Рассмотрим процесс измерения длин отрезков. Из множества отрезков выбирают какой-нибудь отрезок е и принимают его за единицу длины. На отрезке а от одного из его концов откладывают последовательно отрезки, равные е, до тех нор, пока это возможно. Если отрезки, равные е, отложились п раз и конец последнего совпал с концом отрезка а, го говорят, что значение длины отрезка а есть натуральное число п, и пишут: а = пе. Если же отрезки, равные е, отложились п раз и остался еще остаток, мепыпий <?, то на нем откла-

¹ I-

дывают отрезки равные сц = — е. Если они отложились точно п 1 раз,

то тогда а — п, /ме и значение длины отрезка а есть конечная де­сятичная дробь. Если же отрезок е* отложился ч\ раз и остался еще остаток, меньший в\, то на нем откладывают отрезки, равные

е₂=-1—е. Если представить этот процесс бесконечно продолжен- 100

ным, то получим, что значение длины отрезка а есть бесконечная десятичная дробь.

Итак, при выбранной единице длина любого отрезка выражается положительным действительным числом.

Верно и обратное: если дано положительное действительное число п, П\П2--, то, взяв его приближение с определенной точностью и проведя построения, отраженные в записи этого числа, получим отрезок, численное значение длины которого есть дробь П, Л|Л₂... .

Таким образом, мы доказали одно из основных свойств длин отрезков:

1. При выбранной единице длины длина любого отрезка вы­ражается положительным действительным числом, и для каждого положительного действительного числа есть отрезок, длина кото­рого выражается этим числом.

Заметим, что в тех случаях, когда в результате измерения получается бесконечная десятичная дробь, значение длины отрезка оказывается приближенным, хотя и может быть сколь угодно точ­ным, и его можно представлять в виде обыкновенной дроби.

Докажем еще ряд известных свойств длин отрезков. Будем считать при этом, что длины измеряются с помощью одной и той же единицы длины.

2. Если два отрезка равны, то численные значения их длин также равны, и обратно: если численные значения длин двух отрезков равны, то равны и сами отрезки.

а = Ь о т_е (а) = т_с (Ь).

Действительно, если отрезки равны, то, измеряя их длины, мы будем откладывать одно и то же число единиц, равных е, и долей единицы е, значит, численные значения длин равных отрезков совпадут.

Обратно: если численные значения длин двух отрезков равны, то они описывают процесс построения равных отрезков.

3. Если данный отрезок есть сумма нескольких отрезков, то чис­ленное значение его длины равно сумме численных значений длин отрезков слагаемых, и обратно: если численное значение длины отрезка равно сумме численных значений нескольких отрезков, то и сам отрезок равен сумме этих отрезков.

с — а-\-Ь о т_е(с) = т_е (а) -+- т_е (Ь).

Пусть а и Ь — длины отрезков, а -2- и их численные значения,

т. е. а = -у«, Ь=-^-е. Чтобы получить значение суммы а + 6, от­кладываем сначала р отрезков, равных — е. а потом еще <7 таких отрезков. В результате получаем, что длина суммы данных отрезков выражается числом 288

ц + 6 = р-—е + ^- —<? = —е + —?=(—+—) е. ^г п ^ II П ¹ П \ п ¹ п )

Обратно: сумма означает, что отрезок -^-е надо откла­

дывать р + д раз, т. е. получаем отрезок [р-{-д)-^-е = р'-~е-{-

±-а•— е = — е+— е — а-\-Ь. Следовательно, если численные зна- ¹ ’ п п п

чения длин отрезков складываются, то складываются и соответ­ствующие отрезки.

4. Если длины отрезков а и Ь таковы, что Ъ—ха, где х — положительное действительное число и длина а измерена при помощи единицы е, то, чтобы найти численное значение длины Ь при единице е, достаточно число х умножить на численное значение длины а при единице е.

Ь = ха о ш_с {Ь) — х • Шс {а).

Пусть Ь—ха и а=—е. Тогда Ь=х-—ещ х-—)е, т. е.

■' п п \ /I /

ш, (Ь)=х-т_е (а).

Произведение означает, что отрезок е надо откладывать

Х’~ раз, т. е. е=х-~е = ха = Ь.

5. При замене единицы длины численное значение длины уве­личивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.

Пусть имеются две единицы длины е и е\, и пусть в\=ке, т. е. новая единица в к раз больше старой. Если длина отрезка а

при единице е имела значение —, т. е. а=—е, то при единице е\

^Г II П

числовое значение длины отрезка а уменьшится в к раз:

а —— е=——!— <?| —Аг е\, а число в к раз меньше числа —. п п к пк пк ^г п

Из доказанных свойств длин отрезков вытекают еще следующие:

6. а> Ь т_е(а)> т,.(Ь).

7. с = а — Ь о т_е(с)= /п.. (а) — т_с (Ь).

8. х = а:Ь о х = т_с(а):т_с(Ь).

Рассмотренные свойства позволяют сравнение длин отрезков и действия над ними сводить к сравнению н действиям над соответствующими численными значениями длин этих отрезков. На­пример, 12 м<12,3 м, так как 12<12,3; 7,8 см + 3,2 см =(7,8 + + 3,2)см=11 см; 17-3 дм =(17-3) дм = 51 дм.

В начальном курсе математики длины отрезков измеряют, строят отрезки заданной длины, сравнивают длины отрезков, производят над ними действия.

Сравнивая длины отрезков, выполняя сложение, вычитание и

-6с,

а

в А

1дм

1см

А

Н

о

*—

■з

Рис. 156 Рис. 157

другие действия над длинами, неявно используют теоретические по­ложения, изложенные в данном пункте.

Так, выполняя задание «Начерти два отрезка: первый длиной I дм, а второй на 1 см длиннее», учащиеся неявно пользуются тем, что для каждого положительного числа есть отрезок, длина которого выражается этим числом. Отрезков длиной 1 дм существует бесконечное множество (поэтому каждый ученик и может начертить «свой» отрезок), но все они равны между собой.

Второй отрезок, который на 1 см длиннее первого, можно пост­роить по-разному. Например, на луче ОА можно сначала отложить отрезок ОВ длиной 1 дм, а затем от точки В отложить отрезок ВА\, длина которого 1 см (рис. 156). А можно сначала найти сумму 1 дм + 1 см = 10 см + 1 см =(10+1) см = 11 см, а затем построить отрезок длиной 11 см.

Выполнение задания «Начерти два отрезка: длина первого 6 см. а второй в 2 раза длиннее. Чему равна длина второго отрезка?» связано с умножением длины на число. Задание может быть выпол­нено различными способами.

/ способ. Строят отрезок длиной 6 см, а затем на луче ОА по­следовательно откладывают 2 равных отрезка длиной 6 см (рис. 157). Полученный отрезок ОА является искомым, его длина равна 2>6 см = 12 см.

II способ. Находят длину второго отрезка: 2-6 см=(2-6) см =

— 12 см, а затем строят 2 отрезка, один длиной 6 см, а другой длиной 12 см.

Задание «Отрезок длиной 12 см разделить на 2 равные части» предполагает умение делить длину на натуральное чисто. Мы не выделили такой операции, поскольку деление длины на натуральное

число п равносильно умножению ее на дробь — . В связи с этим

^П 1

деление 12 см на 2 равносильно умножению 12 см на 12 см=(-|— 12^ см = (12:2) см.

Вообще деление длины на натуральное число сводится к делению численного ее значения на данное натуральное число.

Упражнения

1. Известно, что расстояние от пункта А до пункта В равно 6 км, от В до С 8 км. Чему может быть равно расстояние от А до С?

2. Существуют ли три точки Л, В и С, такие, что

1. ЛС=15 см, Л В = 8 см, ВС — 7 см;

2. ЛС = 8 см, ЛВ = 25 см, ВС = 40 см;

3. ЛС = 24 см, ЛВ = 30 см, ВС = 40 см?

3. На прямой отметьте точки Л, В, С и О так, чтобы расстояние от Л до В равнялось 2 см, расстояние от В до С — 1,5 см, от С до О — 1 см. Найдите длины отрезков АВ, Ай, ВС, СО, если за единичный отрезок принять:

I) отрезок СВ; 2) отрезок ЛВ; 3) отрезок ВС; 4) отрезок ЛВ.

4. Расстояние от дома до школы 400 м, а расстояние от-дома до

вокзала 0,9 км. Во сколько раз расстояние от дома до вокзала больше расстояния от дома до школы?

5. Длину стола измеряли сначала в сантиметрах, потом в деци­метрах. В первом случае получили число на 108 большее, чем во втором. Чему равна длина стола?

6. Численное значение длины отрезка, измеренной при помощи единицы е\, равно 6, а измеренной при помощи единицы ег — равно 4. В каком отношении находятся между собой единицы длины е\ и во?

7. Постройте отрезок, длина которого 4,6 е. Каким будет числен­ное значение длины этого отрезка, если единицу длины е\

1. увеличить в 3 раза; 2) уменьшить в 1,5 раза?

8. Какие действия над длинами будут выполнять учащиеся на­чальных классов при решении следующих задач:

1. Начерти квадрат со стороной 5 см. Найди сумму длин всех сторон этого квадрата.

2. Сумма длин всех сторон квадрата 28 см. Чему равна длина стороны этого квадрата?

3. На детскую простыню идет 2 м полотна, а на пододеяльник — в 2 раза больше, чем на простыню. Сколько полотна пойдет на 8 комплектов, состоящих из одной простыни и одного пододеяльника?

4. В одном куске было 24 м ткани, а в другом — на 8 м меньше. Из всей этой ткани сшили несколько одинаковых платьев, расходуя на каждое по 4 м ткани. Сколько сшили платьев?

5. За три дня турист проехал 3220 км. В первый день он проехал четвертую часть всего пути, во второй день 1920 км, а в третий день остальной путь. Сколько километров проехал турист в третий день?

6. Отрезок длиной 6 см увеличили в несколько раз и получили отрезок длиной 18 см. Во сколько раз увеличили отрезок?

101. Площадь фигуры и се измерение

Понятие о площади фигуры имеет любой человек: мы говорим о площади комнаты, площади земельного участка, о площади поверхности, которую надо покрасить, и т. д. При этом мы понимаем, что если земельные участки одинаковы, то площади их равны; что у большего участка площадь больше; что площадь квартиры слага­ется из площади комнат и площади других ее помещений.

Это обыденное представление о площади используется при ее оп­ределении в геометрии, где говорят о площади фигуры. Но геомет­рические фигуры устроены по-разному, и поэтому, когда говорят о площади, выделяют особый класс фигур. Например, рассматри­вают площади многоугольников и других ограниченных выпуклых фигур, или площадь круга, или площадь поверхности тел вращения и т. д. Мы будем говорить только о площади многоугольников и ограниченных выпуклых плоских фигур. Такая фигура может быть составлена из других. Например, фигура Р, изображенная на рисунке 158, составлена из фигур Р\, Рз и Рз■ Говоря, что фигура

составлена (состоит) из фигур Р\, Рз Р_п, имеют в виду, что она

является их объединением и любые две данные фигуры не имеют общих внутренних точек.

Определение. Площадью фигуры называется неотрица­тельная величина, определенная для каждой фигуры так, что:

1. равные фигуры имеют равные площади;

2. если фигура составлена из конечного числа фигур, то ее площадь равна сумме их площадей.

Если сравнить данное определение с определением длины отрез­ка, то увидим, что площадь характеризуется теми же свойствами, что и длина, но заданы они на разных множествах: длина — на множестве отрезков, а площадь — на множестве плоских фигур.

Условимся площадь фигуры Р обозначать 5 (Р).

Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, за единицу площади принимают площадь квадрата со стороной, равной единичному отрезку е, т. е. отрезку, выбранному в качестве единицы длины. Площадь квадрата со стороной е обозначают е². Например, если длина стороны единичного квадра­та т, то его площадь т .

Измерение площади состоит в сравнении площади данной фигуры с площадью единичного квадрата е². Результатом этого сравнения является такое число х, что 5 (Р) — хе². Число х называют числен­ным значением площади при выбранной единице площади.

Так, если единицей площади яйляется см², то площадь фигуры, приведенной на рисунке 159, равна 5 см².

Рассмотрим некоторые приемы измерения площадей фигур.

Одним из приемов, опирающихся непосредственно на определе­ние площади, является измерение площади при помощи палетки — сетки квадратов, нанесенной на прозрачный материал.

Допустим, что на фигуру Р, площадь которой надо измерить (рис. 160), наложена сетка квад­ратов со стороной е. Тогда по отношению к этой фигуре можно выделить квадраты двух видов:

1. 

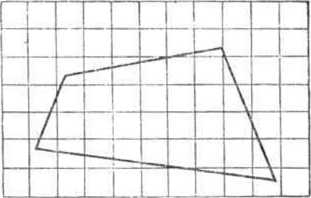
   Рис. 100

   квадраты, которые цели­ком лежат внутри фигуры Р\

2. квадраты, через которые проходит контур фигуры и которые лежат частью вне, частью внутри фигуры Р.

Пусть квадратов первого вида окажется т, а квадратов второ­го вида — п. Тогда, очевидно, площадь фигуры Р будет удовлет­ворять условию те² <5 {Р)<{гп +п) е². Числа т и т-\-п будут приближенными численными значениями измеряемой площади: пер­вое число с недостатком, второе — с избытком.

Как видим, такая палетка позволяет измерить площадь фигуры Р лишь с невысокой точностью. Чтобы получить более точный ре­зультат, можно уплотнить первоначальную сеть квадратов, разде­лив каждый из них на более мелкие квадраты. Можно, например,

I „

построить сеть квадратов со стороной е>=—с. В результате мы

получим другие приближенные значения площади фигуры Р, причем с большей точностью.

Описанный процесс можно продолжить. Возникает вопрос: су­ществует ли такое действительное число, которое больше всякого приближенного результата измерения, взятого с недостатком, и мень­ше всякого приближенного результата измерения, взятого с избыт­ком, и которое может быть точным численным значением измеряе­мой площади? В математике доказано, что при выбранной единице площади такое число существует для всякой площади, оно единствен­но и удовлетворяет свойствам 1 и 2, указанным в определении площади.

Прием измерения площадей фигур при помощи палетки имеет ограниченное применение, его можно использовать лишь для не­больших площадей, он громоздок по исполнению. Поэтому в мате­матике с момента ее возникновения шел поиск косвенных путей измерения площади посредством измерения длин сторон, высот и других отрезков, принадлежащих фигуре. Например, численное зна­чение площади прямоугольника находят, перемножив численные значения длин его сторон.

Из определения площади и сути ее измерения вытекают из­вестные правила сравнения площадей и действий над ними. Рас­смотрим некоторые из них.

/. Если фигуры равны, то равны численные значения их пло­щадей (при одной и той же единице площади).

Фигуры, у которых площади равны, называют равновеликими.

Рис. 162

5 (Р,) = в СМ* 5(Р_г) = всм*

Рнс. 161

Например, прямоугольник и треугольник на рисунке 161 равнове­лики.

2. Если фигура Р составлена из фигур Р\, Рп, Р_п, то числен­ное значение площади фигуры Р равно сумме численных значений площадей фигур РР₂, Р_п (при одной и той же единице площади ).

Найдем, например, площадь фигуры Р, изображенной на рисунке 162. Эту фигуру можно рассматривать как составленную из двух прямоугольников Р| и Р2 (это разбиение фигуры Р образовано при помощи прямой /). Тогда 5 (/^-') = 5 (Е|)-{-5 (/^гг) = 3 см-1 см-+- + 3 см-4 см = 3 см²-|-12 см² = (3+12) см²=15 см².

2. При замене единицы площади численное значение площади увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.

Выразим, например, 5 см² в квадратных дециметрах. Известно, что 1 см² = 0,01 дм², и, следовательно, 5 см² = 5-1 см² = 5-(0,01 дм²) = = (5-0,01) дм² = 0,05 дм².

В начальных классах происходит первоначальное знакомство уча­щихся с понятием площади фигуры. Представление о площади фигуры формируется на основе сравнения фигур: так как квадрат

помещается внутри круга (рис. 163), то его площадь меньше площади круга, а площадь круга больше площади квадрата.

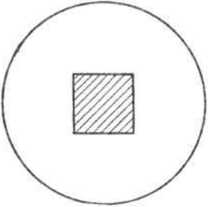
Учащиеся знакомятся с приемом измере­ния площадей фигур при помощи палетки — сети квадратов со стороной 1 см. Наложив палетку на фигуру, учащиеся определяют:

1. число квадратов, которые целиком лежат внутри фигуры;

2. число квадратов, через которые про­ходит контур фигуры.

Рнс. юз Если, например, оказалось, что первых

квадратов 26, а вторых 18, то число квадратов, через которые проходит контур фигуры, т. е. число 18, делят пополам и прибавляют эту половину к числу квадратов, целиком содержащихся внутри фигуры. В результате получают численное значение площади данной фигуры: 26Ц- 18:2«26-(-9 = 35. Значит, 5 (/⁷) = 35 см².

Почему так производят вычисления?

Пусть т — число квадратов, которые целиком лежат внутри фигуры Р, а п — число квадратов, через которые проходит кон­тур фигуры Р. Тогда те¹ <$ (Р)<(т-{- п) с².

Чтобы найти приближенное значение площади фигуры Р, достаточно сложить полученные численные значения площади по недостатку и по избытку и разделить эту сумму пополам

5 {Р)ж ^т+('н+^п) _е² После преобразования получим 5(/^г)« _да/я+рн + я) _е<г _ >т -\_п_ ^2 _^_т | ^ п_{оследнее} выражение озна­чает, что приближенное значение площади фигуры Р равно сумме числа квадратов, которые целиком лежат внутри фигуры Р, и поло­вине числа квадратов, через которые проходит контур этой фигуры,— пришли к школьному правилу определения приближенного числен­ного значения площади фигуры при помощи палетки.

Численное значение площади прямоугольника учащиеся началь­ных классов находят сначала, непосредственно подсчитывая число единичных квадратов, лежащих внутри этого прямоугольника, или используя налетку, а затем используют косвенный способ — перемно­жают численные значения длин сторон прямоугольника.

Упражнения

1. Докажите, что если фигура Р\ содержится в фигуре Я₂, то 5 (Р|)^5 (Р2). При доказательстве используйте свойства площади фигуры, содержащиеся в определении.

2. На рисунке 164 Р=Р|, Р = Р\ и 5(Я) = 3 см², 5(Р) = 2 см². Докажите, используя свойства площади, что 5(Я) = 5 см³.

3. Площадь фигуры Р равна сумме площадей фигур Р\ и Р2? Значит ли это, что фигура составлена из фигур Р\ и Р₂?

4. Два треугольника имеют равные площади. Следует ли из этого, что они равны?

5. Площадь фигуры Р\ больше площади фигуры Р%. Следует ли из этого, что фигура Р₂ целиком содержится в фигуре /д?

6. На фигуру Р наложили на­летку и подсчитали, что внутри р

фигуры Р помещается фигура, Р — Н

составленная из 28 единичных квадратов, а фигура Р уклады­вается внутри фигуры, состоящей Рис. 104

из 35 единичных квадратов. Может ли численное значение площади данной фигуры Г быть равным 27, 3? 29, 6? 32, 8? 35, 4? '

7. 

   Найдите площади фигур, на которые наложена палетка (рис. 165), при условии, что длина стороны квадрата палет-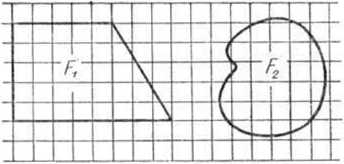

Рис. 165 ки: 1) 1 см; 2) 0,5 см.

8. Начертите круг радиуса 2 см на миллиметровой бумаге и оцените площадь этого круга с помощью двойного неравенства, подсчитывая; 1) квадраты со стороной 1 см; 2) квадраты со стороной 0,5 см; 3) квадраты со сто­роной 0,1 см.

Вычислите площадь этого круга по формуле 5 = лг², приняв л = 3,14.

9. Среди следующих высказываний укажите истинные:

1. Числовые значения площади одной и той же фигуры могут быть различными.

2. Числовые значения площадей неравных фигур могут быть равными.

3. Равновеликие фигуры равны.

10. Докажите, что в одном квадратном дециметре содержится 100 квадратных сантиметров.

11. Известно, что 5(/^г) = 34,78 см². Каким будет численное значение этой площади, если ее измерять в квадратных деци­метрах?

12. Площадь кухни 9 м². Сколько плиток линолеума, имеющих форму квадрата со стороной 3 дм, нужно для покрытия пола в кухне?

13. Площадь прямоугольника равна 12 см², длины его сторон выражаются натуральными числами. Сколько различных прямо­угольников можно построить согласно этим условиям?

14. Длины двух неравных сторон прямоугольника выражаются иррациональными числами. Следует ли из этого, что значение пло­щади данного прямоугольника будет также иррациональным чис­лом?

15. Может ли прямоугольник, длины сторон которого выражают­ся иррациональными числами, быть равновеликим прямоугольнику, длины сторон которого выражаются числами рациональными?

16. Докажите, что если основание прямоугольника увеличить в 2 раза, а высоту уменьшить в 2 раза, то площадь прямоуголь­ника не изменится.

Верен ли будет этот вывод в том случае, если основание прямоугольника увеличить на 20%, а высоту уменьшить на 20%?

17. Решите нижеприведенные задачи и объясните, какие операции над площадями были при этом выполнены:

1. Площадь прямоугольника в 3 раза больше площади квадрата. Длина прямоугольника 96 см. Чему равна ширина прямоуголь­ника, если сторона квадрата 48 см?

2. Общая площадь двух земельных участков прямоугольной фор­мы равна 7,4 га. Длина первого участка 250 м, длина второго 150 м. Найдите площадь каждого участка, если ширина первого участка на 40 м больше ширины второго участка.

3. Если длину прямоугольника увеличить на 2 дм, а ширину уменьшить на 5 дм, то получится квадрат, площадь которого будет меньше площади прямоугольника на 50 дм². Определите площадь квадрата.

4. Площадь одной стены комнаты равна 14 м² 90 дм², а смеж­ной стены — 9 м² 80 дм². В комнате имеется окно площадью 3 м² 50 дм² и дверь площадью 2 м² 20 дм². Кроме того, десятая часть стен под потолком не оклеивается обоями. Какую площадь займут обои?