89. Действия над положительными действительными числами

Объединение множества положительных рациональных чисел Р+ и множества положительных иррациональных чисел /₊ называют множеством положительных действительных чисел и обозначают символом 7? + .

Таким образом . *+ = <? + (_)/+. При помощи кругов Эйлера дан­ные множества изображены на рисунке 132.

Любое положительное действительное число может быть пред­ставлено бесконечной десятичной дробью — периодической (если оно является рациональным) либо непериодической (если оно яв­ляется иррациональным).

по избытку.

Рис. 132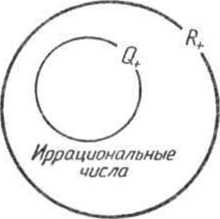

Как известно, действия над положительными рациональными числами сводятся, по существу, к действиям над натуральными числами. А как выполнять действия над действительными чис­лами, представленными бесконечными десятичными дробями? Нельзя ли действия над ними свести к действиям над рациональ­ными числами? Можно, но для этого надо ввести понятие при­ближенного значения действительного числа по недостатку и

Пусть а = л,Л|Л2...я&...— некоторое дей­ствительное число. Приближенным зна­чением числа а по недостатку с точностью до I

называется число а* = я,Л|Лг...л* (т. е. приближенное значение числа а по недостат­ку с точностью до ^ получится, если

взять целую часть числа и первые к цифр после запятой, а все остальные цифры отбросить). Приближенным значением числа а — л,Л|,Л2...л*... по избытку с точностью до

уууг называется число а* = л,Л|«2---«*-Ьуууг (^т- ^е- приближенное значе­ние числа а по избытку с точностью до у^ получится, если в записи

последнюю цифру увеличить на 1).

Для любого действительного числа а справедливо неравенст­во а*<а<а*.

Например, десятичным приближением числа -^/3= 1,73205... по недостатку с точностью до 0,001 является число 1,732,

а по избытку — число 1,733.

Видим, что десятичные приближения действительного числа являются конечными десятичными дробями. На этом и основы­ваются, определяя действия над положительными действитель­ными числами.

Пусть даны действительные числа а и Ь, а* и Ь_к — их приб­лиженные значения по недостатку, а* и Ы, — приближенные зна­чения по избытку.

Определение. Суммой положительных действительных чисел а и 6 называется такое число а + Ь, которое удовлетворя­ет следующему неравенству: а* + 6*<а + 6<а* + 6*.

Найдем, например, сумму с точностью до 0,001.

Возьмем десятичные приближения данных чисел с точностью до 0,0001:

1.4142<л/2< 1,4143,

1,7320 <73< 1,7321.

Тогда 3,1462<л/2 + 73<3,1464, а -у/2+ ->/3 = 3.146.... С точ­ностью до 0,001 сумма ^/2 + л/З равна 3,146.

Определение. Произведением положительных действи­тельных чисел а и Ь называется число а Ь, которое удовлетво­ряет следующим условиям:

Найдем, например, произведение с точностью до 0,1.

Возьмем десятичные приближения данных чисел с точностью до 0,01:

1.41< л/2 < 1.42.

1,73<73<1.74.

Тогда 2,4393^-у/2--у/3<2,4708, а -у/2-л/3 = 2,4... . С точностью до 0,1 произведение л/2-^/3 равно 2,4.

Для любых положительных действительных чисел выполняются следующие равенства:

1. Докажите, что числа 4,7 и 4,8 являются десятичными прибли- жениями соответственно по недостатку и по избытку числа д/23 с точностью до 0,1. -з

2. Проверьте, истинно ли неравенство: 1) 3,6^3-2-3,7;

2. 7,26<7-^<7,27.

3. Десятичное приближение д/24, взятое из таблицы квадратных корней с точностью до 0,001, равно 4,583. Проверьте, как произ­ведено округление: с недостатком или с избытком.

4. Архимед установил, что отношение длины окружности к ее диа­метру больше, чем 3^-, и меньше, чем 3-|-. Найдите десятичные

приближения этих дробей с точностью до: а) 0,01; б) 0,001.

5. Известно, что числа а = 3,6272..., 6 = 5,2814.... Найдите три первых десятичных знака суммы а+ 6.

6. Известно, что л: = 0,35..., у = 0,82... . Найдите первый десятич­ный знак произведения *•//.

7. Проверьте вычисления: 1) 20,8-1--^=21,4(36); 2) 220—“= = 219,(36).