§ 3. Математические доказательства 35

13. Дедуктивные рассуждения 35

14. Простейшие схемы дедуктивных рассуждений 41

15. Неполная индукция ’³ 44

16. Способы доказательства истинности высказываний 47

§ 4. Текстовые задачи и их решение 51

17. Понятие текстовой задачи 51

18. Способы решения текстовых задач 53

111111111111111111111III1111 ^>мъ° 56

(л п пс=л п(в п с). (Л1)В)ис=Л11(вис). 79

2) С=((а, (Ь, <Г), (а, с)); 96

□ □ □ о о о о 137

"^{еотрииатель}' ОООООКН8В2 145

«О О О О 141

^□□□□□□000 «О О О О О О 139

□ □□□□□□□□□□□ 158

& . 226

I „ 295

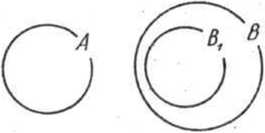
= В|ЦВ{ и, следовательно, п (В)=п (В\[)В[). По- Рис. 91

скольку множества В\ и В\ не пе­ресекаются, то по определению А~В. суммы п {В) = п (В,) + л (В\) (*). Но по условию В|~+ значит, п{В\) — п{Я). Если число элемен­тов в множестве В\ обозначить через с, то равенство (*) можно записать в виде 6 = а + с, т. е. из того, что а<Ь, следует, что Ь = а-\-с■ Нетрудно убедиться и в справедливости обратного утверждения.

Пришли к другому определению отношения «меньше»:

Число а меньше числа 6 тогда и только тогда, когда существует такое натуральное число с, что а + с = 6.

Как, пользуясь этим определением, объяснить, что 3<7? 3<7, поскольку существует такое целое неотрицательное число 4, что 3 + 4 = 7.

Этот способ определения отношения «меньше» через сложение также используется в начальном курсе математики. Об этом говорит наличие пар записей 5+1=6, 6>5; 7+1=8, 7<8.

Рассмотрим еще один способ сравнения чисел.

Пусть-а < Ь. Тогда про любое натуральное число х можно сказать, что если х^а, то х<Ь. Это значит, что при а<Ь отрезок натурального ряда Ы_а является собственным подмножеством отрезка Ыь. Справедливо и обратное утверждение.

Таким образом, получаем еще одно определение отношения «меньше»:

Число а меньше числа Ь тогда и только тогда, когда отрезок натурального ряда /У_а является собственным подмножеством отрез­ка этого ряда ДО»:

а<Ь«ЫУ_ас:ДО» и ДО_а=+ДО» .

Например, справедливость неравенства 3<7 с этих позиций мож­но объяснить тем, что (1, 2, 3)с:{1, 2, 3, 4, 5, 6, 7).

Данная трактовка понятия «меньше» позволяет сравнивать числа, опираясь на знание их места в натуральном ряду.

Этот способ сравнения чисел также используется в начальном обучении математике: число, которое при счете встречается раньше, всегда меньше числа, которое идет позднее.

Упражнения

1. Объясните тремя способами, почему: 1) 3<6; 2) 0<5.

2. Используя определение отношения «меньше» через сложение, докажите, что для любых натуральных чисел а, Ь, с справедливо утверждение: «Если а<Ь, то а + с<& + с».

3. Почему отношение «меньше* упорядочивает множество целых неотрицательных чисел, а отношение «непосредственно следовать за» нет?

4. Приведите примеры двух заданий из учебников математики для начальных классов, в которых отношение «меньше* («больше») рассматривается с теоретико-множественных позиций.

39. Вычитание

Рассмотрим задачу, которую решают первоклассники’

«Около школы посадили 8 деревьев — берез и рябин.. Берез 3. Сколько рябин посадили около школы?»

Чтобы ответить на вопрос задачи, надо из 8 вычесть 3: 8 — 3 = 5. Но как объяснить, почему здесь использовано вычитание чисел, а не другое действие? Представим условие задачи наглядно, изобразив каждое дерево, посаженное около школы, кружком (рис. 93).

Среди посаженных деревьев 3 березы — на рисунке выделим их, зачеркнув каждый кружок, изображающий березу. Тогда остальные деревья — рябины. Их столько, сколько будет, если из 8 вычесть 3, т. е. 5.

Видим, что решение данной задачи тесно связано с выделением из данного множества подмножества и нахождением числа элементов в дополнении этого подмножества, т. е. вычитание чисел оказы­вается связанным с операцией дополнения подмножества.

Определение. Разностью целых неотрицательных чисел а и Ь называется число элементов в дополнении множества В до множе­ства А при условии, что п (А)—а, п (В)=Ь и ВаА:

а — Ь = п(А\В), где а — п(А), Ь = п{В), В с: А

Пример. Объясним, используя данное определение, Что 7 — 4 = = 3. 7 — это число элементов некоторого множества А, 4 — число элементов множества В, которое является подмножеством множе­ства А. Возьмем, например, множества А = [х, у, г, I, р, г, 5}, В = {дг, у, г, /}. Найдем дополнение множества В до множества А: А\В = {р, г, 5}. Получаем, что п(А\В)=3. Следовательно, 7-4 = 3.

Очевидно, в качестве таких множеств А и В, что п(А) = 7, п[В)=4 и ВаА, можно было выбрать множества, отличные от рассматриваемых, поскольку разность а — Ь не зависит от выбора множеств А и В, удовлетворяющих условиям п(А) = а, п(В) = Ь и ВаА.

Но всегда ли существует

"^{еотрииатель}' ОООООКН8В2

Из того, что ВаА, следует, Рис 93

что н(В)<1п(Л). Значит, разность а — Ь це­лых неотрицательных чисел а и Ь, таких, что а = п(А), Ь = п(В) и Вс=Л, существует только тогда, когда а.

Действие, при полощи которого находят разность а — Ь, называется вычитанием,чис­ло а — уменьшаемым, число Ь — вычитае­мым.

Часто, чтобы проверить правильность выполнения действия вычитания, мы обра­щаемся к сложению. Почему? Очевидно потому, что существует связь между дейст­виями вычитания и сложения. ,

Пусть даны целые неотрицательные числа а и Ь, такие, что а = п(А), Ь = п(В) и Вс=Л, и пусть разность этих чисел есть число элементов дополнения множества В до множества А, т. е. а — Ь = = п(А\В).

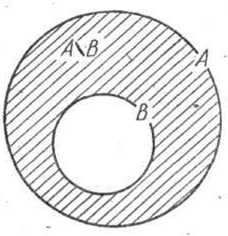
На кругах Эйлера множества А, В, А\В изображаются так, как на рисунке 94. Известно, что Л = В1Д.Д\В), откуда п(Л) = — п (В|ДЛ\В)). Так как ВП(Л\В)= 0, то имеем п (А) — п (ВЦ(А\В)) = = п (В)-\-п (А\В) — Ь-\-(а — Ь). Следовательно, получаем, что а = = Ь-\-(а — Ь), т. е. разность а — Ь есть такое число, сумма которого и числа Ь равна числу а.

Установленный факт дает возможность по-другому дать опреде­ление разности.

Определение. Разностью целых неотрицательных чисел апЬ называется такое целое неотрицательное число с, сумма которого и числа Ь равна а.

Таким образом,

Мы показали, что из определения разности целых неотрица­тельных чисел как числа элементов дополнения одного множества до другого вытекает ее определение через сумму. Можно доказать и обратное утверждение. /

а — Ь=соа — Ь-\~с

Говорят, что действие вычитания является обратным сложе­нию.

Докажем, исходя из второго определения разности, следующие теоремы:

Теорема. Разность целых неотрицательных чисел а и Ь суще­ствует тогда и только тогда, когда Ь^а.

Доказательство. Если а = Ь, то а — Ь=\), и, следовательно, разность а — Ь существует.

Если Ь<.а, то по определению отношения «меньше» существует такое натуральное число с, что а = Ь + с. Тогда по определению разности с = а — Ь, т. е. разность а — Ь существует.

Если разность а — Ь существует, то по определению разности найдется такое целое неотрицательное число с, что а = Ь-\-с. Если 136 .

с = 0, то а = Ь\ если с>0, то Ь<а по определению «меньше». Итак,

.

Теорема. Если разность целых неотрицательных чисел а и Ь существует, то она единственна.

Доказательство. Предположим, что существуют два зна­чения разности а — Ь: а — Ь=С\ и а — Ь = С2. Тогда по определению разности имеем я = 6 + С| и а = Ь + С2. Отсюда следует Ь-\-С[ = Ь + -\-с2 и, значит, С\ =Сг.

В начальном курсе математики первоначально вычитание целых неотрицательных чисел рассматривается на основе драктиче- ских упражнений, связанных с выделением подмножества данного множества и образованием нового множества — дополнения выде­ленного подмножества. При этом теоретико-множественная термино­логия и символика не используются. Главным средством раскры­тия теоретико-множественного смысла вычитания является реше­ние простых задач.

Суть решения одной такой задачи проанализирована в начале пункта.

Связь вычитания со сложением устанавливается при изучении темы «Как найти неизвестное слагаемое». Определение понятия вычитания как действия, обратного сложению, в явном виде не дается, но подчеркивается, что «вычитание связано со сложением: вычесть из числа 40 число 16 — значит найти такое число, которое При сложении его с числом 16 дает в сумме 40. Это число 24. Значит, 40—16 = 24».

Упражнения

1. Дайте теоретико-множественное истолкование следующим равенствам: 1) 7 — 5 = 2; 2) 3 — 3 = 0; 3) 4 — 0 = 4.

2. В учебнике по математике для начальной школы приведено пра­вило: «Для проверки вычитания к разности прибавляют вычитае-

. мое. Если решение правильное, то получится уменьшаемое». Каково"'* теоретическое обоснование этого правила?

3. Приведите примеры двух заданий из учебников по математи­ке для начальных классов, при выполнении которых используется условие существования разности целых неотрицательных чисел.

4. Объясните, почему нижеприведенные задачи решаются при помощи вычитания:

1. У пруда росло 9 осин. 4 осины спилили. Сколько осин ос­талось у пруда?

2. Вова и Лида нарисовали 9 домиков. Лида нарисовала 4 доми­ка. Сколько домиков нарисовал Вова?

5. Составьте 3 задачи, решение которых записывается в виде равенства 12 — 8 = 4. На основании какого теоретического положе­ния это возможно?

При решении задач и в практической деятельности часто требуется не только установить, что число а меньше (или больше) числа Ь, но и узнать, на сколько число $ меньше (или больше) числа Ь.

Каков смысл отношений «меньше на» и «больше на»?

Пусть а и Ь — целые неотрицательные числа, такие, что а = л (Л), Ь — п(В), и установлено, что а<Ь. Это значит, что в множестве В можно выделить собственное подмножество Вравномощное множеству Л, и множество В\В^ не пусто. Пусть п (В\В\)=с (сФ0). Тогда в множестве В элементов столько же, сколько в множестве Л, да еще с элементов. В этом случае говорят, что число а меньше числа Ь на с или что число Ь больше числа а на с.

Так как с = п (В\В_{), где то с = Ь — а. Следовательно,

чтобы узнать, на сколько одно число меньше или больше другого, надо из большего числа вычесть меньшее.

Рассмотрим, например, задачу: «У школы посадили 4 дуба и 9 лип. На сколько больше посадили лип?»

Согласно сформулированному правилу ответ на вопрос нахо­дится при помощи вычитания: 9 — 4 = 5 (лип). Однако возникает недоразумение: можно ли из 9 лип вычитать 4 дуба? Дело в том, что в данном случае из 9 лип вычитают 4 липы. Чтобы убедить­ся в этом, изобразим дубы кружками, а липы квадратиками (рис. 95).

Чтобы ответить на вопрос задачи, выделим в множестве лип подмножество 2\, равномощное множеству дубов (на рисунке это множество показано фигурной скобкой). Тогда остальные липы образуют дополнение множества 2\ до множества 2 и их число равно разности 9 и 4.

Отношения «больше на» и «меньше на» встречаются и в зада­чах другого вида.

Рассмотрим, например, такую задачу: «У школы посадили 4 дуба, а лип на 5 больше. Сколько лип посадили?»

В задаче речь идет о двух множествах деревьев: множестве дубов и множестве лип. Обозначим их О и 2. Известно, что л(Д) = 4, а число элементов в множестве 2 надо найти, зная, что в нем на 5 элементов больше, чем в Д. Последнее означает, что л (2) — я(Д) = 5, откуда л (2) — 5 +л (Д) = 5Ц-4 = 9. Можно дать более подробное пояснение, воспользовавшись рисунком 95.

«О О О О

г :

Рис. 95

^□□□□□□000 «О О О О О О

Рве. 96

Так как в множестве 2 на 5 элементов больше, чем в множестве О, то это значит, что в множестве 2 столько же элементов, сколько в О, да еще 5 элементов. Другими словами, множество 2 можно рассматривать как объединение двух множеств 2\ и 2ч, таких, что 2| ~ Ь и п (2г)=5. Поскольку множества 2\ и 2ч не имеют' общих элементов, то п (2)=л (2| [}2ч)=п {2()-\-п (2г) = 4 + 5 = 9.

Обратимся теперь к задаче: «У школы посадили 9 лип, а дубов на 3 меньше. Сколько посадили дубов?»

В ней так же, как и в предыдущей, речь идет о двух множе­ствах: множестве лип (2) и множестве дубов (О), но известно, что л (2) = 9, а число элементов в множестве О надо найти, зная, что в нем на 3 элемента меньше, чем в 2. Последнее означает, что л(2) —л(0) = 3, откуда п (О) = п (2) — 3 = 9 — 3 = 6.

Используя рисунок 96, решение этой задачи можно выполнить так: поскольку дубов на 3 меньше, чем лип, то лип на 3 больше, чем дубов, поэтому, удалив из множества 2 подмножество, состоящее из трех элементов, получим множество, равномощное множеству О. п (0) = 9 —3 = 6.

Естественно, что в начальной школе при решении приведенных в пункте задач объяснение будет выглядеть иначе, но суть его от этого не изменится.

Заметим, что предложение «5 больше 2 на 3» нельзя запи­сать кратко, используя знак «>», поскольку для записи отношения «больше на» (так же как и для отношения «меньше на») нет специального знака. Знак «>» служит для обозначения отноше­ния «больше», а знак «<» — отношения «меньше».

Упражнения

1. Объясните, почему нижеприведенные задачи решаются при помощи сложения:

1. У Коли 7 марок, а у Саши на 3 марки больше. Сколько марок у Саши?

2. В парке 8 голубых елок. Их на 2 меньше, чем берез. Сколько берез в парке?

2. Объясните, почему следующие задачи решаются при помощи вычитания:

1. Таня нашла 9 грибов, а Лида на 4 гриба меньше. Сколько грибов нашла Лида?

2. У школы посадили 4 дуба и 9 лип. На сколько меньше по­садили дубов?

3. У Нины 6 тетрадей, а у Коли 4. На сколько тетрадей больше у Нины, чем у Коли?

3. Составьте 2 простые задачи, в которых рассматривалось бы отношение «меньше на» и решение записывалось в виде равен­ства 10 — 2 = 8.

4. Составьте 2 простые задачи, в которых рассматривалось бы отношение «больше на» и задача решалась при помощи сложения.